RSA安全性问题

标签：

加密：C=M^e（mod n）

解密：M=C^d（mod n）

安全性基础：

穷举法攻击：

1.攻击者设计一个M，C=M^e（mod n）

2.d的个数至多有n-1个，尝试使用每个d破解，如果M’=C^d‘（mod n）=M，d’是解

3.设p，q分别为100位（十进制），则n-1约200位（十进制）   n=10²⁰⁰

4.假定每秒可以做一亿次搜索（10⁸），每年可以搜索10⁸*60*60*24*365=3*10¹⁵

搜索10²⁰⁰个密钥的时间为100²⁰⁰/（3*10¹⁵）=3*10¹⁵=10¹⁸⁴年

计算上不可行。

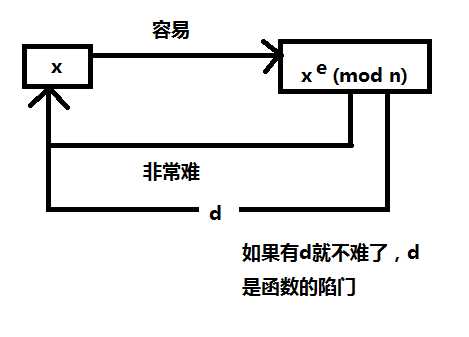
分析RSA锁结构

d=e^-1mod (Φ(n))  即 de=1 mod (Φ(n))

问题为：已知e，Φ(n)未知，求d

如果Φ(n)知道，则求d就很容易了

问题变为：已知n，求Φ(n)

求法1：直接求，当n很大，计算Φ(n)很困难，不可行

求法2：利用n=pq，（p，q是素数），Φ(n)=（p-1）（q-1）计算很容易

问题变为：已知n，求n=pq，（p，q是素数） 即数的素分解问题

素因子分解的复杂性：

目前因子分解速度最快的方法的时间复杂度是exp（sqrt（ln n lnln n））

2007年3个机构（EPFL,波恩大学，日本电话电报公司）设计的计算机集群成功分解307位十进制的数2¹⁰³⁹-1

所以说RSA的安全性依赖于分解大数的难度？数学上还未能证明只有分解大数n才能从C和e中计算出M（即RSA的安全性与大数分解等价）。所以说上面的说法只是一个假定，不过目前为止也未能证明它的错误。

即便无法有效破解RSA算法，但还有一些别的办法是针对协议进行攻击的。

A窃听B的通讯，获得c=m^e mod n，A的目标是解出m

1.A选一个r，计算x=r^e mod n （即r=x^d mod n）

2.计算y=xc mod n

3.计算t=r^-1 mod n

4.A让B在y上签名，u=y^d mod n

5.A计算 tu mod n=r^-1y^d mod n

　　　　　　　　　=r^-1x^d c^d mod n

　　　　　　　　　=r^-1r^ed c^d mod n

　　　　　　　　　=c^d mod n = m

问题出现在B对不明信息签名。

怎么解决：从算法上无法解决，主要措施是采用好的公钥协议

1.工作过程中实体不轻易对其他实体任意产生的信息加解密，不对一无所知的信息签名

2.对其他实体送来的随机文档签名时首先对文档作HASH处理

还有其他一些问题：

1.如果p，q比较接近

2.系统采用公共模数，n一直不变

这样的系统在数学上被证明更容易被破解。

寻找合适的素数：

1.尾数除法，取一数p，用2到该数的平方根之间的每一个素数去除该数，如果都不能整除，该数就是素数。

2.Fermat方法

3.Lehmann测试法

4.Miller-Rabin测试法

...

RSA安全性问题

标签：

原文地址：http://www.cnblogs.com/13jhzeng/p/5550228.html