Greg and Graph+floyd算法的应用

时间：2014-08-02 18:26:33 阅读：287 评论：0 收藏：0 [点我收藏+]

Greg has a weighed directed graph, consisting of n vertices. In this graph any pair of distinct vertices has an edge between them in both directions. Greg loves playing with the graph and now he has invented a new game:

The game consists of n steps.
On the i-th step Greg removes vertex number xi from the graph. As Greg removes a vertex, he also removes all the edges that go in and out of this vertex.
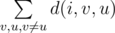Before executing each step, Greg wants to know the sum of lengths of the shortest paths between all pairs of the remaining vertices. The shortest path can go through any remaining vertex. In other words, if we assume that d(i,?v,?u) is the shortest path between vertices v and u in the graph that formed before deleting vertex xi, then Greg wants to know the value of the following sum: $bubuko.com,布布扣$ .

Help Greg, print the value of the required sum before each step.

Input

The first line contains integer n (1?≤?n?≤?500) — the number of vertices in the graph.

Next n lines contain n integers each — the graph adjacency matrix: the j-th number in the i-th line aij (1?≤?aij?≤?105,?aii?=?0) represents the weight of the edge that goes from vertex i to vertex j.

The next line contains n distinct integers: x1,?x2,?...,?xn (1?≤?xi?≤?n) — the vertices that Greg deletes.

Output

Print n integers — the i-th number equals the required sum before the i-th step.

Please, do not use the %lld specifier to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams of the %I64dspecifier.

Sample test(s)

input
1
0
1

output
0 

input
2
0 5
4 0
1 2

output
9 0 

input
4
0 3 1 1
6 0 400 1
2 4 0 1
1 1 1 0
4 1 2 3

output
17 23 404 0 解决方案：可逆向的做，在一个没有点的图中，先加最后删去的那条边，算出总的最短路，以去点边的顺序不断加边，当把边补完时，即求出所有结果。这题啊要对floyd有一定的理解。code:#include<iostream>
#include<cstdio>
#include<cstring>
#define MMAX 550
#define inf -1
using namespace std;
long long Map[MMAX][MMAX];
long long arra[MMAX];
long long r[MMAX];
bool vis[MMAX];
int n,m;
int main()
{
    int a,b,x;
    while(cin>>n)
    {
        memset(vis,false,sizeof(vis));
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
            {
                cin>>Map[i][j];
            }
        for(int i=1; i<=n; i++)
        {
            cin>>arra[i];
        }
        for(int i=n; i>=1; i--)
        {
            vis[arra[i]]=true;
            for(int j=1; j<=n; j++)
                for(int k=1; k<=n; k++)
                {
                    if(Map[j][k]>Map[j][arra[i]]+Map[arra[i]][k])
                    {
                        Map[j][k]=Map[j][arra[i]]+Map[arra[i]][k];
                    }
                }
            long long sum=0;
            for(int j=1; j<=n; j++)
                for(int k=1; k<=n; k++)
                {
                    if(vis[j]&&vis[k])
                    {
                        sum+=Map[j][k];
                    }
                }

           r[i]=sum;
        }
        for(int i=1;i<n;i++){
            cout<<r[i]<<" ";
        }
        cout<<r[n]<<endl;

    }
    return 0;
}

Greg and Graph+floyd算法的应用,布布扣,bubuko.com

Greg and Graph+floyd算法的应用

标签：style http color os io for cti ar

原文地址：http://blog.csdn.net/u012870383/article/details/38349483

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行