标签:
一、梯度检测:
对于函数而言通常有两种计算梯度的方式:
1.数值梯度 (numberical gradient)
2.解析梯度 (analytic gradient )
数值梯度计算通常为:
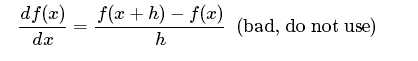
更为常见的是:
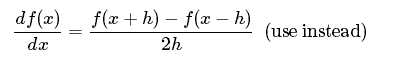
h是一个很小的数,在实际当中通常为1e-5
假设数值梯度为ƒ’a 解析梯度为ƒ’n ,则数值梯度和解析梯度的误差relative error:
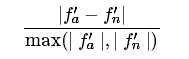
relative error >1e-2 通常情况梯度是错误的
1e-4 < relative error < 1e-2 并不是很好
relative error < 1e-4 对于有拐点的函数是ok的,但是如果没有拐点(如tanh nonlinearities and softmax),1e-4 太高了
relative error 或者更小最好
警告:建议使用双精度来进行梯度检测
有拐点的函数例如 ReLU(max(0,x)) 或者SVM loss
h并不是越小越好,h太小容易出现精度问题,h通常在1e-4到 1e-6
正则化容易将改变原先的梯度,最好是先进行梯度计算,然后在正则化梯度计算
梯度下降检测时不要进行dropout
标签:
原文地址:http://www.cnblogs.com/luxiao/p/5552635.html