标签:
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。而最长公共子串(要求连续)和最长公共子序列是不同的.
最长公共子序列是一个十分实用的问题,它可以描述两段文字之间的"相似度",即它们的雷同程度,从而能够用来辨别抄袭。对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分,往往十分准确。
动态规划法
经常会遇到复杂问题不能简单地分解成几个子问题,而会分解出一系列的子问题。简单地采用把大问题分解成子问题,并综合子问题的解导出大问题的解的方法,问题求解耗时会按问题规模呈幂级数增加。为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组中,这就是动态规划法所采用的基本方法。
算法
动态规划的一个计算两个序列的最长公共子序列的方法如下:
以两个序列 X、Y 为例子:
设有二维数组f[i,j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度,则有:
f[1][1] = same(1,1);
f[i,j] = max{f[i-1][j -1] + same(i,j),f[i-1,j],f[i,j-1]}
其中,same(a,b)当 X 的第 a 位与 Y 的第 b 位相同时为"1",否则为"0"。
此时,二维数组中最大的数便是 X 和 Y 的最长公共子序列的长度,依据该数组回溯,便可找出最长公共子序列。
该算法的空间、时间复杂度均为O(n^2),经过优化后,空间复杂度可为O(n)。
【问题】 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题,设A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”为它们的最长公共子序列。不难证明有以下性质:
(1) 如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
(2) 如果am-1!=bn-1,则若zk-1!=am-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列;
(3) 如果am-1!=bn-1,则若zk-1!=bn-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有am-1=bn-1,则进一步解决一个子问题,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一个最长公共子序列;如果am-1!=bn-1,则要解决两个子问题,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
求解:
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
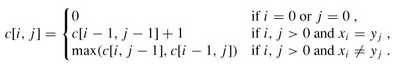
回溯输出最长公共子序列过程:
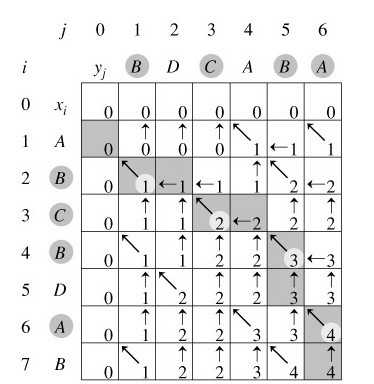
我来说明下此图(参考算法导论)。在序列X={A,B,C,B,D,A,B}和 Y={B,D,C,A,B,A}上,由LCS_LENGTH计算出的表c和b。第i行和第j列中的方块包含了c[i,j]的值以及指向b[i,j]的箭头。在c[7,6]的项4,表的右下角为X和Y的一个LCS<B,C,B,A>的长度。对于i,j>0,项c[i,j]仅依赖于是否有xi=yi,及项c[i-1,j]和c[i,j-1]的值,这几个项都在c[i,j]之前计算。为了重构一个LCS的元素,从右下角开始跟踪b[i,j]的箭头即可,这条路径标示为阴影,这条路径上的每一个“↖”对应于一个使xi=yi为一个LCS的成员的项(高亮标示)。
所以根据上述图所示的结果,程序将最终输出:“B C B A”。
算法分析:
由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m + n)。
#include <stdio.h> #include <string.h> #define MAXLEN 100 void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN]) { int i, j; for (i = 0; i <= m; i++) c[i][0] = 0; for (j = 1; j <= n; j++) c[0][j] = 0; for (i = 1; i <= m; i++) { for (j = 1; j <= n; j++) { if (x[i - 1] == y[j - 1]) { c[i][j] = c[i - 1][j - 1] + 1; b[i][j] = 0; } else if (c[i - 1][j] >= c[i][j - 1]) { c[i][j] = c[i - 1][j]; b[i][j] = 1; } else { c[i][j] = c[i][j - 1]; b[i][j] = -1; } } } } void PrintLCS(int b[][MAXLEN], char *x, int i, int j) { if (i == 0 || j == 0) return; if (b[i][j] == 0) { PrintLCS(b, x, i - 1, j - 1); printf("%c ", x[i - 1]); } else if (b[i][j] == 1) PrintLCS(b, x, i - 1, j); else PrintLCS(b, x, i, j - 1); } int main(int argc, char **argv) { char x[MAXLEN] = { "ABCBDAB" }; char y[MAXLEN] = { "BDCABA" }; int b[MAXLEN][MAXLEN]; int c[MAXLEN][MAXLEN]; int m, n; m = strlen(x); n = strlen(y); LCSLength(x, y, m, n, c, b); PrintLCS(b, x, m, n); return 0; }
分两个部分:(参考:http://blog.csdn.net/v_july_v/article/details/6695482)
1)计算最优值 LCSLength()
计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度,b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的,这在构造最长公共子序列时要用到。最后,X和Y的最长公共子序列的长度记录于c[m,n]中。
由算法LCS_LENGTH计算得到的数组b可用于快速构造序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列。首先从b[m,n]开始,沿着其中的箭头所指的方向在数组b中搜索。
这种方法是按照反序来找LCS的每一个元素的。由于每个数组单元的计算耗费Ο(1)时间,算法LCS_LENGTH耗时Ο(mn)。
2)构造最长公共子序列 PrintLCS()
在算法LCS中,每一次的递归调用使i或j减1,因此算法的计算时间为O(m+n)。
算法的改进:参考:http://blog.csdn.net/v_july_v/article/details/6695482
变形题型:参考:http://www.cnblogs.com/zhangchaoyang/articles/2012070.html(最大子序列、最长递增子序列、最长公共子串、最长公共子序列、字符串编辑距离)
/** * 第一步:论证是否是动态规划问题 * 首先要证明最长公共子序列问题是动态规划问题,即符合动态规划算法的两个特点:最优子结构和重叠子问题 * 最优子结构: * 记:Xi=﹤x1...xi﹥即X序列的前i个字符 (1≤i≤m)(前缀) Yj=﹤y1...yj﹥即Y序列的前j个字符 (1≤j≤n)(前缀) * 假定Z=﹤z1...zk﹥∈LCS(X , Y)。 * 若xm=yn(最后一个字符相同),则问题化归成求Xm-1与Yn-1的LCS(LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1)。 * 若xm≠yn,则问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为:max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。 * 由于上述当xm≠yn的情况中,求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度,这两个问题不是相互独立的:两者都需要求LCS(Xm-1,Yn-1)的长度。 * 另外两个序列的LCS中包含了两个序列的前缀的LCS,故问题具有最优子结构性质。 * 重叠子问题: * 在计算X和Y的最长公共子序列时,可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列, * 而这两个子问题都包含一个公共子问题,即计算Xm-1和Yn-1的最长公共子序列,因此最长公共子序列问题具有子问题重叠性质。 * * 第二步:建立递归式 * 用c[i][j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>,Yj=<y1, y2, …, yj>。建立递归关系如下: * 0 if i=0||j=0 * c[i][j]= c[i-1][j-1]+1 if i,j>0&&x[i]==y[j] * max(c[i][j-1],c[i-1][j]) if i,j>0&&x[i]!=y[j]; */ public class LCS { /**第三步:计算最优值 * 计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作为输入。 * 输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度,b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的, * 这在构造最长公共子序列时要用到。最后,X和Y的最长公共子序列的长度记录于c[m,n]中。 * 在这里可以将数组b省去。事实上,数组元素c[i,j]的值仅由c[i-1,j-1],c[i-1,j]和c[i,j-1]三个值之一确定,而数组元素b[i,j]也只是用来指示c[i,j]究竟由哪个值确定。 * 因此,在算法LCS中,我们可以不借助于数组b而借助于数组c本身临时判断c[i,j]的值是由c[i-1,j-1],c[i-1,j]和c[i,j-1]中哪一个数值元素所确定,代价是Ο(1)时间。 * @param x * @param y * @return */ public int[][] lcsLength(char x[],char y[]){ int m = x.length; int n = y.length; int [][]c = new int[m+1][n+1]; for(int i = 0;i<m+1;i++) c[i][0]=0; for(int j = 0;j<n+1;j++) c[0][j]=0; for(int i = 1;i<=m;i++){ for(int j = 1;j<=n;j++){ //i,j从1开始,所以下面用i-1和j-1使得可以从数组0元素开始 if(x[i-1]==y[j-1]){ c[i][j] = c[i-1][j-1]+1; }else if(c[i-1][j]>=c[i][j-1]){ c[i][j]=c[i-1][j]; }else{ c[i][j]=c[i][j-1]; } } } return c; } /**第四步:构造最长公共子序列 * lcs函数用来构造最长公共子序列,它使用在计算最优值中得到的c数组可以快速的 * 构造序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列。 * @param c * @param x * @param i * @param j */ public void lcs(int c[][],char x[],int i,int j){ if(i==0||j==0)return; if(c[i][j]==(c[i-1][j-1]+1)){ lcs(c,x,i-1,j-1); //注意c的长度要比x大1 System.out.println(x[i-1]); }else if(c[i][j]==c[i-1][j]){ lcs(c,x,i-1,j); }else{ lcs(c,x,i,j-1); } } //测试 public static void main(String args[]){ char x[]={‘A‘,‘B‘,‘C‘,‘B‘,‘D‘,‘A‘,‘B‘}; char y[]={‘B‘,‘D‘,‘C‘,‘A‘,‘B‘,‘A‘}; LCS lcs = new LCS(); int [][]c = lcs.lcsLength(x, y); lcs.lcs(c, x, x.length, y.length); } }
参考:
http://www.cnblogs.com/zhangchaoyang/articles/2012070.html
http://blog.csdn.net/yysdsyl/article/details/4226630
标签:
原文地址:http://www.cnblogs.com/ranjiewen/p/5559490.html