标签：
作为一个机器学习入门级选手，写这篇是抱着很大的谨慎态度的，svm的确是涉及到较多数学知识的一章，不甚好理解。此篇仅作为给自己的一个学习记录。
依然按惯例，svm的原生方法解决的分类问题，以二分类为例。我们现在有很多条样本数据，类别标签属于两类，一类是正例，一类是负例。svm的核心想法是找到一个间隔最大的超平面，可以将样本分成两类。超平面听起来很玄，但是最简单的形式大家都知道，就是二维平面里的直线。众所周知，二维平面中的直线方程：
wx+b=0,如果我们知道了w和b，那么就知道了一个确定的直线。那么重要的问题就是，这样的直线也许有无穷条，哪一个才是离样本点间隔最大的那一条呢？
首先要定义一个间隔的概念，定义超平面（w,b）关于样本点（xi,yi）的函数间隔为
,而定义超平面关于整个训练集的函数间隔为前面所有间隔里最小的那个。
为了使得间隔不受w和b的影响，将函数间隔单位化，定义出几何间隔：
,同样的，定义超平面关于整个训练集的几个间隔是所有里面最小的那个。
现在，svm方法想找到的就是，求得几何间隔最大的分离超平面。注意这句话，这里指的几何间隔，是关于整个训练集的那个，最小的那个，如何尽量使最小的那个最大！！
表述成数学公式（我也很不愿意，但是有利于解释）：
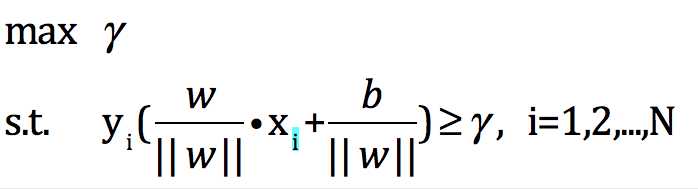根据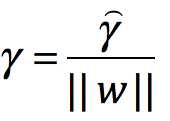
,再令函数间隔为1，注意到最大化
和最小化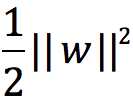
是等价的，因此，我们得到了最最基本的一个svm里面的约束最优化公式
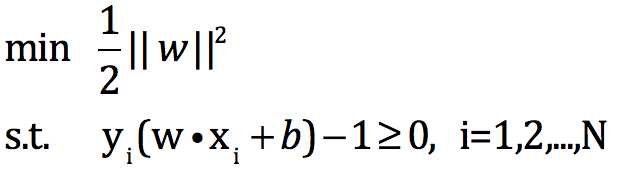
后续的故事，绝大部分就以此展开了，先写到这。
标签：
原文地址：http://www.cnblogs.com/lvlvlvlvlv/p/5561796.html
