题目链接:http://poj.org/problem?id=3119
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 431 | Accepted: 177 |
Description
A determined army on a certain border decided to enumerate the coordinates in its patrol in a way to make it difficult for the enemy to know what positions they are referring to in the case that the radio signal used for communication is intercepted. The
enumeration process chosen was the following: first it is decided where the axes x and y are; then, a linear equation that describes the position of the border relative to the the axes (yes, it is a straight line) is defined; finally,
all points on the Cartesian plane that is not part of the border are enumerated, the number 0 being attributed to the coordinate (0, 0) and starting from there numbers being attributed to integral coordinates following a clockwise
spiral, always skipping points that fall on the border (see Figure 1). If the point (0, 0) falls on the border, the number 0 is attributed to the first point that is not part of the border following the specified order.
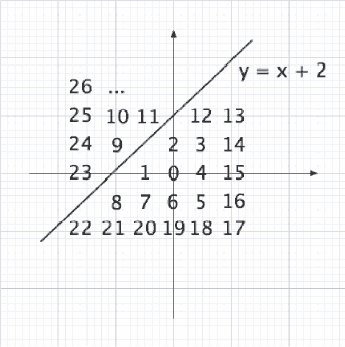
Figure 1: Enumeration of points of integral coordinates
In fact the enemy does not have to know either what position the army is referring to or the system used to enumerate the points. Such a project, complicated the life of the army, once that it is difficult to determine whether two points are on the same side of the border or on opposite sides. That is where they need your help.
Input
The input contains several test cases. The first line of the input contains an integer N (1 ≤ N ≤ 100) which represents the quantity of test cases. N test cases follow. The first line of each test case contains two integers a and b (?5 ≤ a ≤ 5 and ?10 ≤ b ≤ 10) which describe the equation of the border: y = ax + b. The second line of each test case contains an integer K, indicating the number of queries that follow it (1 ≤ K ≤ 1000). Each one of the following K lines describes a query, composed by two integers M and N representing the enumerated coordinates of two points (0 ≤ M, N ≤ 65535).
Output
For each test case in the input your program should produce K + 1 lines. The first line should contain the identification of the test case in the form Caso X, where X should be substituted by the case number (starting from 1).
The K following lines should contain the results of the K queries made in the corresponding case in the input, in the form:
Mesmo lado da fronteira(The same side of the border)or
Lados opostos da fronteira(Opposite sides of the border)
Sample Input
2 1 2 10 26 25 25 11 24 9 23 28 25 9 25 1 25 0 9 1 23 12 26 17 1 2 12 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12
Sample Output
Caso 1 Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Lados opostos da fronteira Lados opostos da fronteira Lados opostos da fronteira Lados opostos da fronteira Lados opostos da fronteira Caso 2 Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Lados opostos da fronteira Mesmo lado da fronteira Mesmo lado da fronteira Lados opostos da fronteira
Source
题意:
给出一条直线,试判断再给出的点是否在直线的两侧;在两侧就输出“Lados opostos da fronteira”;在同侧就输出“Mesmo lado da fronteira”;
当然所给的点不是坐标,而是一个数字, 这个数字按照一定的顺序有一个固定坐标,我们需要先把这两个数字的坐标按照给定的顺序找出来在判断在同侧还是异侧;
代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int xx[4] = {-1,0,1,0};//顺序左、上、右、下
int yy[4] = {0,1,0,-1};
struct tt
{
int x, y;
}nod[70017];
int main()
{
int t;
int a, b;
int n;
int cas = 0;
scanf("%d",&t);
while(t--)
{
printf("Caso %d\n",++cas);
scanf("%d%d",&a,&b);
int x = 0, y = 0;//原点为起始点
int num = 0;
int flag = 0;//标记
if(b != 0)//原点不在直线上
{
nod[num].x = x;
nod[num].y = y;
num++;
}
flag++;
int ff = 0;
x += xx[ff];
y += yy[ff];
ff = (ff+1)%4;//四个方向一循环
int cont = 0;
int limit = 1;
while(num <= 65535)//先跑出每个点所在的位置
{
if(a*x+b != y)//当前点不在直线上
{
nod[num].x = x;
nod[num].y = y;
num++;
}
cont++;
x += xx[ff];
y += yy[ff];
if(cont == limit)
{
ff = (ff+1)%4;
cont = 0;
flag++;
}
if(flag == 2)//因为所走的矩形是一个长方形
{//需要连续走两次步数相同的边
flag = 0;
limit++;
}
}
scanf("%d",&n);
int num1, num2;
int flag1,flag2;
for(int i = 0; i < n; i++)
{
scanf("%d%d",&num1,&num2);
if(nod[num1].x*a+b < nod[num1].y)
flag1 = -1;
else
flag1 = 1;
if(nod[num2].x*a+b < nod[num2].y)
flag2 = -1;
else
flag2 = 1;
if(flag1 * flag2 > 0)//同一边
printf("Mesmo lado da fronteira\n");
else
printf("Lados opostos da fronteira\n");
}
}
return 0;
}poj 3117 Friends or Enemies?(模拟),布布扣,bubuko.com
poj 3117 Friends or Enemies?(模拟)
原文地址:http://blog.csdn.net/u012860063/article/details/38356097