标签:
上一篇说过,本篇我会给大家介绍传说中的“傅立叶变换”。首先要回答的就是什么是傅立叶变换?傅立叶变换在21世纪的今天我们每个人每天都在使用:手机信号从3G开始,到现在的4G、将来的5G所用的CDMA协议的核心就是对电磁波信号进行傅立叶变换。傅立变换的作用就是把杂乱无章的信号分解成一系列有规律的信号相加。打个通俗点的比喻,就像是烧菜。一锅东北乱炖烧好后,往锅里一看,乱七八糟什么都有。但是仔细查看,可以发现里面有5个豆角、2个土豆、10片西红柿。聪明的你也许能猜到烧菜的人想对你传达一个暧昧信息。
傅立叶变换是傅立叶同学在19世纪发明出来的,他在他的论文里说任何周期函数都可以分解成为许多个三角函数的和,并给出了计算公式。结果论文发表到审核的时候,当时的数学牛人中的大牛人,拉格朗日,拉普拉斯等纷纷表示看不懂,傅立叶同学是不是脑子坏特了。虽然后来几十年里傅立叶变换的理论被人们逐渐认可,但也一直没有实际应用,因为它实在是太复杂了,根本没人算得出来。直到20世纪八十年代,计算机和网络开始在世界上普及,有了计算机的计算能力和无线网络通讯的实际需求,傅立叶变换又重新走进数学家的视野。
傅立叶变换在大学课程中属于积分变换。我说过积分变换是我在大学里众多完全没听懂的数学课之一。工作后耳边也时常听到这个词,每次的感觉都是不明觉厉的。也尝试多次去了解傅立叶变换是怎么回事,却每每看到一大堆更加陌生的词汇:时域、频域、频谱……结果越看越迷惑,最后总落得个一知半解的下场,草草了事。
失之东隅,收之桑榆。我因为别的原因学习了线性代数,没想到在学正交矩阵的时候,傅立叶变换竟成了继最小二乘法之后的例题,而我竟然完全看明白了!不一样的配方,却还是熟悉的味道。这也是数学的魅力之所在,只要问题有一个答案,不管你从什么方向有什么方向去计算,最后总是能得到一样的结果。而不像语文,从这个角度看可以看到什么;从当时的语境可以看到作者想表达什么思想;从出题老师的标语答案我们可以得到什么样的解题思路。看一本书,一千个读者眼里有一千个沙士比亚;解一个方程,一万个解法永远只能得到一个正确答案。
故事讲完了,下面开始上课
在上一节课里我们讲了最小二乘法:对于一个N维空间之外的任意一个点,我们可以找到这个点在N维空间里最接近的一个点,即这个点在空间里的投影。而如果我们可以找到这个N维空间里的一组基,那这个点的投影可以很容易地通过内积求出。
N维空间的点是N维向量。前一节讲小明的物理实验,他测出了5个点,就可以构成一个五维向量(X1,X2,X3,X4,X5),如果小明足够的勤劳,他就不止可以测5个点,而是50或500个点,那就构成了500维的向量(X1,X2,X3…X500)。如果我们继续增加点的数量直至无穷大,那这些本来离散的点最终会连接成一条曲线,曲线上的每个点都符合某个函数f(x),对于某个范围内x都可以得到y=f(x)。f(x)就是一个无限维度的向量,或者是无限维空间里的一个点,而所有世界上可能出现的函数加在一起就构成了无限维度的空间。
有了点和空间,我们自然就会联想到像小明的实验一样,在空间里找一条直线,和点f(x)最为接近的函数g(x)。我们又知道,如果我们能知道这个空间的一组基把这个空间的点表示为:
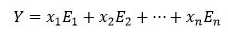
那任意点X在Y上的投影就是X与每一个基的内积乘上基求和:
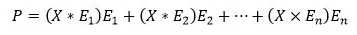
既然对所有的N维空间都适用,那对于无限维空间的函数应该也同样适用才是。那函数的内积又是什么?我们知道对于N维向量内积定义把向量每一维单独相乘并求和:
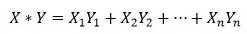
以此类推,那无限维向量函数内积就应该是把函数上的每个点相乘求和,如果给x限定一个范围[0, 1],那
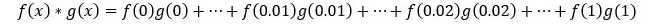
这个东西怎么算?数学家说了,离散值累积用加法,连续值累积用积分!
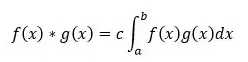
有了内积,接下来要找空间的基,即空间中的一组相互正交并且长度为1的向量。正交就是向量相互内积为0,长度为1就是向量自身内积为1
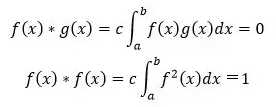
傅立叶同学所做的就是找到了满足这两条件的一组好基友,他们是一组限定范围在[-π,π]之间且c=1/π的三角函数
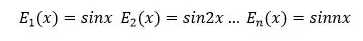
那么任意f(x)在由傅立叶同学所指定的空间里的最接近的函数就是
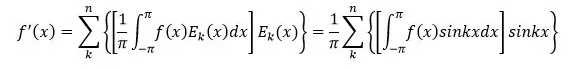
(傅立叶变换里除了sinnx项外还有对称的cosnx项,两者原理相同,此处偷懒省略)
这里面的n最大可以是无限大,而且n越大,f’(x)与f(x)之间的差别越小。由于正弦函数sin(x)是一个周期函数,所以不管怎么加,他们的结果也只能是周期函数。
有了傅立叶变换,牛郎就可以轻松把原本没有任何规律的电波以正弦函数为原材料炖成一锅东北乱炖:
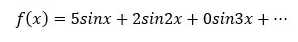
而身处遥远的织女银河对岸的收到这一电波,经过傅立叶变换分解,就可以解读牛郎所要传达的信息5、2、0!
这是不是一件很美妙的事情呢?

我的线性代数随笔系列-从二元一次方程组到傅立叶变换至此完结。原本只是抱着深入学习处理计算机三维图形的空间变换的目的来学习线性代数的。之前也看过一些别的线性代数书,基本翻个两章就没有学习的兴趣的。这些特地在网上作了一番搜索,这本由美国Steven J. Leon写的线性代数得票挺高,遂入手了一本。
此书从线性方程组讲起,我发现我竟然看懂了。随着难度逐渐深入,我越看越有信心,也越来越有兴趣。直到有一天,我看完了正交矩阵,最后一个例题竟然是傅立叶变换。顿时头皮发麻,这不是大学数学三座大山之一么,可是它为什么会出现的线性代数书中?仅仅出于好奇,我继续看了下去,例题从最小二乘引出,定义了函数线性空间,傅立叶变换水到渠成。区区两页A4大小的书页就把这个我曾经认为神(经病)一样的公式讲得清清楚楚,而且是那么的自然、那么的优雅,那一瞬、我对作者的崇拜、对数学的敬畏涌上心头。那时这篇笔记的名字-从二元一次方程到傅立叶变换就停留在我的脑中。
当然这本书到这里没并有结束,后面还有三分之一的篇幅讲了矩阵特征值,我也获益良多。但始终没有前半本书那样给我如此大的冲击力。所以我的随笔也就到此,当然还有一部分原因是后来的内容相比前一半离我们的生活更加遥远。
后来就是猫馆长的公众号开张。作为一个有文艺情怀理科生,我当然也要写点什么,这篇笔记便得以落地。我想以最朴实的向人阐述数学之美,最初一篇二元一次方程似乎作到了这一点,就连一些文科生都表示没有难度,看来小学数学老师是大家的真爱。第二篇坐标变换,难度上升到中学,文科生开始放弃了,就连理科生也抓耳挠腮,中学数学老师需要反思。第三篇最小二乘法,是大学工科数学内容,所有人都对我表示了呵呵。今天这是最后一篇,难度更上一层楼,却是对我个人冲击最大、直接导致这篇随笔诞生的原因。却不知是几家欢乐几家愁?
《线性代数》随笔系列首发于微信公众号:龙猫图书馆,这是由猫馆长发起的小资文艺青年聚集之所,欢迎关注。

标签:
原文地址:http://www.cnblogs.com/edisonlovecola/p/linear-algebra-4.html