标签:
问题描述:栈是常用的一种数据结构,有n个元素在栈顶端一侧等待进栈,栈顶端另一侧是出栈序列。你已经知道栈的操作有两种:push和pop,前者是将一个元素进栈,后者是将栈顶元素弹出。现在要使用这两种操作,由一个操作序列可以得到一系列的输出序列。请你编程求出对于给定的n,计算并输出由操作数序列1,2,…,n,经过一系列操作可能得到的输出序列总数。
分析:之前就有看过这种问题。就是火车进站问题,判断序列是否合法,当时是用STL栈做的。这个题只需统计次数,那么,方法就十分简便了,递归和动归都可以实现,当然用栈模拟当然也OK。值得一提的是网上看到的一个分析方法(引自石家庄铁道大学 刘莉等论文)
1 引 言
在实际应用和数据结构课程的教学中,栈作为一种基本结构非常重要[1][3][4][6]。已知给定序列,求出栈序列的数目、求所有出栈的序列、以及判断某个序列是否为合法的出栈序列[5][7],这类问题经常出现。在[3]中,对出栈序列的计数问题给出了介绍性的说明,由于结果的证明需要用到生成函数,[3]也只是直接给出了结论。本文提出使用“两点之间路径计数”的方法解决出栈序列的计数问题,在此基础上可以求所有出栈的序列,以及判断某个序列是否为合法的出栈序列。
2 问题分析
两点之间路径计数的问题
问题:假设A、B两点之间所有道路如图1中的方形网格线(5×5),规定从A到B只能够向右或向上移动,求A点到B点有几条路。

图1 两点之间路径计数问题的路径图
分析:因为规定从A到B只能够向右或向上移动,因此任意一点只能从该点的左邻点或下邻点到达,例如,任意一点C点只能从D点或E点到达。因此,从A点到C点的路只能由这两部分组成:①从A点到D点,再从D点到C点;②从A点到E点,再从E点到C点。
结论1:A点到任意一点C的路径数目=从A点到D点(C的左邻点)的路径数目+从A点到E点(C的下邻点)的路径数目
其中,由于A点正上方的点没有左邻点,而且问题中已规定从A到B只能够向右或向上运动,所以A点到A点正上方点的路径数目为1。同理,A点到A点正右方点的路径数目为1。
根据结论1,将A点到任意一点的路径数目求出,如图1中网格线交点处的数字所示。
栈的操作与两点之间路径计数问题的操作的比较
栈的操作有两种:入栈、出栈。其中需要注意的问题有三个:①所有节点入栈之后只能出栈;②栈空时只能入栈;③其它情况下入栈、出栈任意执行。
两点之间路径计数问题的操作有两种:向右移动、向上移动。其中需要注意的问题有三个:①移到最右边后只能向上移;②移到最上边只能向右移;③其它情况下上移、右移任意执行。
由以上分析可见,栈的操作与两点之间路径计数问题的操作有很大的相似性,不妨将入栈和右移相关联,出栈和上移相关联。但是,这样关联之后,由于两个问题并不等价(例如,图1中的D点,按照栈的操作是不可到达的),所以需要对图1中的所有点进一步分析。
对操作关联后图1中点的分析
首先,在图1中添加A点到B点的对角虚线。这条虚线将所有的点分成三类:①虚线上的点;②虚线左上方的点;③虚线右下方的点。
其次,按照两点之间路径计数问题规定的操作容易得出:①从A点移到虚线上每一个点时,所执行的右移操作次数和上移操作次数相等;②从A点移到虚线左上方每一个点时,所执行的右移操作次数小于上移操作次数;③从A点移到虚线右下方每一个点时,所执行的右移操作次数大于上移操作次数。
再次,由于栈操作过程中的任意时刻必须有:入栈操作次数≥出栈操作次数(取等号时栈空)。
很明显,图1中虚线左上方的点按照栈的操作是不可到达的,虚线上的点恰好是栈空时的状态,虚线右下方的点按照栈的操作都可以到达,所以考虑修改图1中的路径图。
改进后的路径图及规则
将图1中虚线左上方的点去掉后如图2所示(5×5方形网格线的下三角)。

图2 改造后的的路径图
规定:从A到B只能够向右或向上移动,右移为入栈操作,上移为出栈操作。
根据2.3的分析可得结论2:
① 从A点到A点正右方的点的路径数目 = 1;
② 从A点到每一行最左的点(考虑B点,不考虑A点)的路径数目 =从A点到该点的下邻点的路径数目;
③ 从A点到其它任意一点C的路径数目=从A点到D点(C的左邻点)的路径数目+从A点到E点(C的下邻点)的路径数目;
④ 按照栈的操作从A点开始到B点,图2中的所有点都是可到达的;
⑤ 4个节点的入栈、出栈操作完全包含在图2中;
⑥ 将⑤扩展得:N个节点的出栈、入栈操作完全包含在(N+1)×(N+1)方形网格线的下三角中。
在此仅对结论2第⑤点作一些说明:首先A点和对角线上的其它点表示栈空,只能入栈(右移);其次,移到最右的竖边时所有的元素都已经入栈,只能出栈(上移);再次,B点为最终状态,不能入栈也不能出栈;最后,其它的点可以任意入栈(右移)、出栈(上移)。所以4个节点的入栈、出栈操作完全包含在图2中。
从结论2中可以看到栈的操作与两点之间路径计数问题的操作在图2中是等价的。根据结论2,将A点到任意一点的路径数目求出,如图2中网格线交点处的数字所示,图2中虚线箭头表示了执行结论2第①点,图2中实线箭头表示了执行结论2第③点。
结论2推广
将结论2加以推广得结论3:对于如图2的形式((N+1)×(N+1)方形网格线的下三角),规定从A到B只能够向右或向上移动,右移为入栈操作,上移为出栈操作,所求A点到B点的路径数目就是N个节点出栈序列的数目,并且从A点到B点的每一条路都代表一种出栈序列。
3 设计实现
求N个节点出栈序列数目的算法在具体实现时,采用由下向上逐行处理,每一行从左至右逐点处理的方法。此外,在 计算当前行的值时,只需要使用上一行的值;在计算各行中的每一个值时左邻点的值为数组中当前元素的前一个元素,下邻点为数组中当前元素,把数组中当前元素 的前一个元素加到当前元素上就求出了当前点的值,所以在具体实现时,只使用一个数组来保存当前行的值即可。由于最后一行只有一个数,也是该行的第一个数, 根据结论2第③点可知该数在倒数第二行中已经计算出来,所以该行不用计算,直接取上一行计算结果中的最后一个数即可。
4 结论
该方法简单方便,不需要记忆任何公式[3],特别适合没有组合数学基础的人员。另外,根据图2还可以设计算法将入栈、出栈的操作序列求出来,这样就可以得到所有的出栈序列。同时根据图2也可以判断某个序列是否为合法的出栈序列,可以解决[5][7]中车厢调度问题。
代码:分为递归和这个论文的算法求解
1、递归版本
#include<iostream>
using namespace std;
int num,n;
//sz表示当前栈大小,i是指向等待调度序列的指针
void calcuNum(int i,int sz){
if(i>n){//所有序列都已处理完毕
num++;
return;
}
calcuNum(i+1,sz+1);//入栈
if(sz>0)//出栈
{
calcuNum(i,sz-1);
}
}
int main()
{
cin>>n;
calcuNum(1,0);
cout<<num;
return 0;
}
2、两点路径问题
#include<iostream>
#include<stack>
using namespace std;
int num,n;
//sz表示当前栈大小,i是指向等待调度序列的指针
void calcuNum(int i,int sz){
if(i>n){//所有序列都已处理完毕
num++;
return;
}
calcuNum(i+1,sz+1);//入栈
if(sz>0)//出栈
{
calcuNum(i,sz-1);
}
}
void path(){
int s[n+1][n+1];
for(int i=0;i<=n;i++) s[0][i]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i < j) s[i][j] = s[i-1][j]+s[i][j-1];
if(i == j) s[i][j] = s[i-1][j];
}
}
num = s[n][n];
}
int main()
{
cin>>n;
path();
cout<<num;
return 0;
}
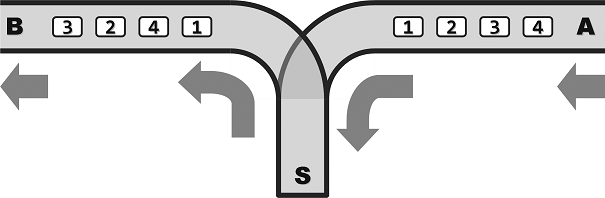
某列车调度站的铁道联接结构如Figure 1所示。
其中,A为入口,B为出口,S为中转盲端。所有铁道均为单轨单向式:列车行驶的方向只能是从A到S,再从S到B;另外,不允许超车。因为车厢可在S中驻留,所以它们从B端驶出的次序,可能与从A端驶入的次序不同。不过S的容量有限,同时驻留的车厢不得超过m节。
设某列车由编号依次为{1, 2, ..., n}的n节车厢组成。调度员希望知道,按照以上交通规则,这些车厢能否以{a1, a2, ..., an}的次序,重新排列后从B端驶出。如果可行,应该以怎样的次序操作?
共两行。
第一行为两个整数n,m。
第二行为以空格分隔的n个整数,保证为{1, 2, ..., n}的一个排列,表示待判断可行性的驶出序列{a1,a2,...,an}。
若驶出序列可行,则输出操作序列,其中push表示车厢从A进入S,pop表示车厢从S进入B,每个操作占一行。
若不可行,则输出No
下面,是之前我在UVa上做的题解法(不完善)
#include <iostream>
#include<stack>
using namespace std;
int const MAX = 1000;
int testOrder(int n)
{
stack<int> train;
int ch[MAX];
int curA=1,curB=1;
for(int i =1; i<=n; i++){
cin>>ch[i];
if(ch[i] ==0){
return 0;
}
}
while(curB<=n){
if(ch[curB] == curA){
curB++;
curA++;
}else if(!train.empty() && ch[curB] == train.top()){
train.pop();
curB++;
}else if(curA<=n){
train.push(curA++);
}else{
cout<<"No"<<endl;
return 1;
}
}
cout<<"Yes"<<endl;
return 1;
}
int main()
{
int n;
cin>>n;
do{
while(testOrder(n)==1);
cin>>n;
if(n!=0) cout<<endl;
}while(n != 0);
return 0;
}
标签:
原文地址:http://www.cnblogs.com/swumqw/p/5570817.html