重建二叉树

标签：二叉树的重建

题目描述：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。

假设输入的二叉树的前序遍历和中序遍历的结果中不包含重复的数字

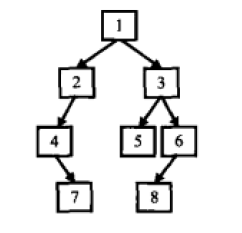
例如，输入前序遍历序列 {1,2,4,7,3,5,6,8} 和中序遍历序列 {4,7,2,1,5,3,8,6} 则重建成如图所示的二叉树，并返回该二叉树的根节点

二叉树的节点定义如下：

struct BinaryTreeNode
{
	T _data;
	BinaryTreeNode<T>* _left;
	BinaryTreeNode<T>* _right;
	
	BinaryTreeNode(const T& x)  //构造函数
	:_data(x)
	, _left(NULL)
	, _right(NULL)
	{}
};

分析：

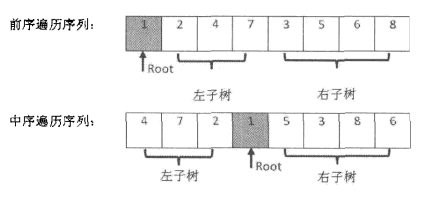
至此，我们找到了左、右子树的前序遍历和中序遍历的结果，我们可以运用此方法继续重建左右子树，因此，我们就可以运用递归解决这个问题了

BinaryTreeNode* Rebuild(const int* prev, const int* in, int length, int& index, int left, int right)
{
	assert(prev && in);

	if (index >= length)
		return NULL;

	BinaryTreeNode* NewNode = new BinaryTreeNode(prev[index]);

	if (left == right)
		return NewNode;
		
	//找到前序节点在中序序列中的位置
	int inIdx = FindIndex(in, prev[index], left, right);
	if(inIdx < 0)
		return NULL;

	NewNode->_left = Rebuild(prev, in, n, ++index, left, inIdx - 1);
	NewNode->_right = Rebuild(prev, in, n, ++index, inIdx + 1, right);

	return NewNode;
}

其中 FindIndex(const int* a, const int& x, int left, int right) 为找到 x 在数组 a 中left到right区间的下标

int FindIndex(const int* a, const int& x, int left, int right)
{
	for (int i = left; i <= right; ++i)
	{
		if (x == a[i])
			return i;
	}

	return -1;
}

注意：参数中的 index 是一个引用，用它来记录当前根节点在前序序列中的下标，开始应该传 0 。

本文出自 “11408774” 博客，请务必保留此出处http://11418774.blog.51cto.com/11408774/1787644

重建二叉树

标签：二叉树的重建

原文地址：http://11418774.blog.51cto.com/11408774/1787644