标签:
本文由zhangbaochong原创,转载请注明出处http://www.cnblogs.com/zhangbaochong/
前面实现简单地形的教程,我们只是绘制了一个网格,这一次我们来学习一下几种基本几何体的绘制,包括平面网格、立方体、圆柱和球体等。
原来在GeometryGenerator类中只给出了CreateGrid一个方法来绘制网格,现在让我们添加其他方法绘制一些几何体。
为了方便绘制几何体方法的调用,GeometryGenerator类我们使用了单例模式。很简单,将构造函数设为private,添加一个GetInstance函数如下:
//单例模式 static GeometryGenerator* GetInstance() { static GeometryGenerator instance; return &instance; }
这只是实现单例模式的一种方法,还有几种实现单例模式的方法就不一一说明了。
下面介绍几种常见几何体的绘制方法(代码均参考dx11龙书)。
网格可以说是最常见同时也是最重要的,像实现地形水面等都离不开网格。生成一个网格首先要给出网格的宽和高,以及在宽和高上划分的格子数。
看龙书中给出的一张图片就明白了:
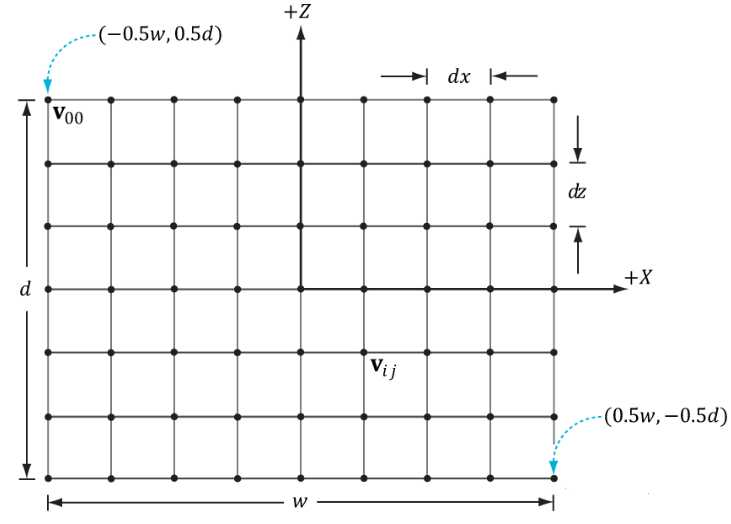
由此,顶点的坐标就很容易生成了。
顶点索引的计算关键是推导出一个用于求构成第i行,第j列的顶点处右下方两个三角形的顶点索引的通用公式。
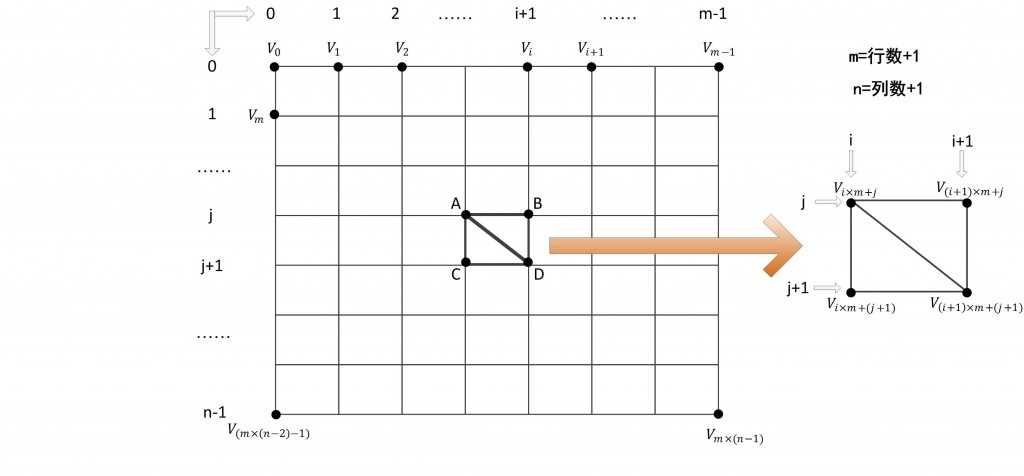
对顶点缓存中的任意一点A,如果该点位于地形中的第i行、第j列的话,那么该点在顶点缓存中所对应的位置应该就是i*m+j(m为每行的顶点数)。如果A点在索引缓存中的位置为k的话,那么A点为起始点构成的三角形ABC中,B、C顶点在顶点缓存中的位置就为(i+1)x m+j和i x m+(j+1)。且B点索引值为k+1,C点索引值为k+2.这样。这样,公式就可以推导为如下:
三角形ABC=【i*每行顶点数+j,i*每行顶点数+(j+1),(i+1)*行顶点数+j】
三角形CBD=【(i+1)*每行顶点数+j,i*每行顶点数+(j+1),(i+1)*行顶点数+(j+1)】
1 void GeometryGenerator::CreateGrid(float width, float height, UINT m, UINT n, MeshData &mesh) 2 { 3 mesh.vertices.clear(); 4 mesh.indices.clear(); 5 //每行顶点数、每列顶点数 6 UINT nVertsRow = m + 1; 7 UINT nVertsCol = n + 1; 8 //起始x、z坐标 9 float oX = -width * 0.5f; 10 float oZ = height * 0.5f; 11 //每一格坐标变化 12 float dx = width / m; 13 float dz = height / n; 14 15 //顶点总数量:nVertsRow * nVertsCol 16 mesh.vertices.resize(nVertsRow * nVertsCol); 17 18 //逐个添加顶点 19 for (UINT i = 0; i < nVertsCol; ++i) 20 { 21 float tmpZ = oZ - dz * i; 22 for (UINT j = 0; j < nVertsRow; ++j) 23 { 24 UINT index = nVertsRow * i + j; 25 mesh.vertices[index].pos.x = oX + dx * j; 26 mesh.vertices[index].pos.y = 0.f; 27 mesh.vertices[index].pos.z = tmpZ; 28 29 mesh.vertices[index].normal = XMFLOAT3(0.f, 1.f, 0.f); 30 mesh.vertices[index].tangent = XMFLOAT3(1.f, 0.f, 0.f); 31 32 mesh.vertices[index].tex = XMFLOAT2(dx*i, dx*j); 33 } 34 } 35 36 //总格子数量:m * n 37 //因此总索引数量: 6 * m * n 38 UINT nIndices = m * n * 6; 39 mesh.indices.resize(nIndices); 40 UINT tmp = 0; 41 for (UINT i = 0; i < n; ++i) 42 { 43 for (UINT j = 0; j < m; ++j) 44 { 45 mesh.indices[tmp] = i * nVertsRow + j; 46 mesh.indices[tmp + 1] = i * nVertsRow + j + 1; 47 mesh.indices[tmp + 2] = (i + 1) * nVertsRow + j; 48 mesh.indices[tmp + 3] = i * nVertsRow + j + 1; 49 mesh.indices[tmp + 4] = (i + 1) * nVertsRow + j + 1; 50 mesh.indices[tmp + 5] = (i + 1) * nVertsRow + j; 51 52 tmp += 6; 53 } 54 } 55 }
立方体的绘制就很简单了,一个立方体只需要提供三维方向上的长度。有一点与之前绘制彩色立方体时不一样的是,我们这里创建立方体用到24个顶点(每个面4个),而之前彩色立方体只用到了8个顶点(每个顶点被3个面共享)。这是因为在后面学习过程中我们需要顶点的法线坐标,而一个顶点相对于其连接的3个面来说,法线完全不同,因此无法共享顶点。

1 void GeometryGenerator::CreateBox(float width, float height, float depth, MeshData &mesh) 2 { 3 mesh.vertices.clear(); 4 mesh.indices.clear(); 5 6 //一共24个顶点(每面4个) 7 mesh.vertices.resize(24); 8 //一共36个索引(每面6个) 9 mesh.indices.resize(36); 10 11 float halfW = width * 0.5f; 12 float halfH = height * 0.5f; 13 float halfD = depth * 0.5f; 14 15 //眼睛面向z轴正方向 16 //构建顶点 17 //前面 18 mesh.vertices[0].pos = XMFLOAT3(-halfW, -halfH, -halfD); 19 mesh.vertices[0].normal = XMFLOAT3(0.f, 0.f, -1.f); 20 mesh.vertices[0].tangent = XMFLOAT3(1.f, 0.f, 0.f); 21 mesh.vertices[0].tex = XMFLOAT2(0.f, 1.f); 22 mesh.vertices[1].pos = XMFLOAT3(-halfW, halfH, -halfD); 23 mesh.vertices[1].normal = XMFLOAT3(0.f, 0.f, -1.f); 24 mesh.vertices[1].tangent = XMFLOAT3(1.f, 0.f, 0.f); 25 mesh.vertices[1].tex = XMFLOAT2(0.f, 0.f); 26 mesh.vertices[2].pos = XMFLOAT3(halfW, halfH, -halfD); 27 mesh.vertices[2].normal = XMFLOAT3(0.f, 0.f, -1.f); 28 mesh.vertices[2].tangent = XMFLOAT3(1.f, 0.f, 0.f); 29 mesh.vertices[2].tex = XMFLOAT2(1.f, 0.f); 30 mesh.vertices[3].pos = XMFLOAT3(halfW, -halfH, -halfD); 31 mesh.vertices[3].normal = XMFLOAT3(0.f, 0.f, -1.f); 32 mesh.vertices[3].tangent = XMFLOAT3(1.f, 0.f, 0.f); 33 mesh.vertices[3].tex = XMFLOAT2(1.f, 1.f); 34 //左侧面 35 mesh.vertices[4].pos = XMFLOAT3(-halfW, -halfH, halfD); 36 mesh.vertices[4].normal = XMFLOAT3(-1.f, 0.f, 0.f); 37 mesh.vertices[4].tangent = XMFLOAT3(0.f, 0.f, -1.f); 38 mesh.vertices[4].tex = XMFLOAT2(0.f, 1.f); 39 mesh.vertices[5].pos = XMFLOAT3(-halfW, halfH, halfD); 40 mesh.vertices[5].normal = XMFLOAT3(-1.f, 0.f, 0.f); 41 mesh.vertices[5].tangent = XMFLOAT3(0.f, 0.f, -1.f); 42 mesh.vertices[5].tex = XMFLOAT2(0.f, 0.f); 43 mesh.vertices[6].pos = XMFLOAT3(-halfW, halfH, -halfD); 44 mesh.vertices[6].normal = XMFLOAT3(-1.f, 0.f, 0.f); 45 mesh.vertices[6].tangent = XMFLOAT3(0.f, 0.f, -1.f); 46 mesh.vertices[6].tex = XMFLOAT2(1.f, 0.f); 47 mesh.vertices[7].pos = XMFLOAT3(-halfW, -halfH, -halfD); 48 mesh.vertices[7].normal = XMFLOAT3(-1.f, 0.f, 0.f); 49 mesh.vertices[7].tangent = XMFLOAT3(0.f, 0.f, -1.f); 50 mesh.vertices[7].tex = XMFLOAT2(1.f, 1.f); 51 //背面 52 mesh.vertices[8].pos = XMFLOAT3(halfW, -halfH, halfD); 53 mesh.vertices[8].normal = XMFLOAT3(0.f, 0.f, 1.f); 54 mesh.vertices[8].tangent = XMFLOAT3(-1.f, 0.f, 0.f); 55 mesh.vertices[8].tex = XMFLOAT2(0.f, 1.f); 56 mesh.vertices[9].pos = XMFLOAT3(halfW, halfH, halfD); 57 mesh.vertices[9].normal = XMFLOAT3(0.f, 0.f, 1.f); 58 mesh.vertices[9].tangent = XMFLOAT3(-1.f, 0.f, 0.f); 59 mesh.vertices[9].tex = XMFLOAT2(0.f, 0.f); 60 mesh.vertices[10].pos = XMFLOAT3(-halfW, halfH, halfD); 61 mesh.vertices[10].normal = XMFLOAT3(0.f, 0.f, 1.f); 62 mesh.vertices[10].tangent = XMFLOAT3(-1.f, 0.f, 0.f); 63 mesh.vertices[10].tex = XMFLOAT2(1.f, 0.f); 64 mesh.vertices[11].pos = XMFLOAT3(-halfW, -halfH, halfD); 65 mesh.vertices[11].normal = XMFLOAT3(0.f, 0.f, 1.f); 66 mesh.vertices[11].tangent = XMFLOAT3(-1.f, 0.f, 0.f); 67 mesh.vertices[11].tex = XMFLOAT2(1.f, 1.f); 68 //右侧面 69 mesh.vertices[12].pos = XMFLOAT3(halfW, -halfH, -halfD); 70 mesh.vertices[12].normal = XMFLOAT3(1.f, 0.f, 0.f); 71 mesh.vertices[12].tangent = XMFLOAT3(0.f, 0.f, 1.f); 72 mesh.vertices[12].tex = XMFLOAT2(0.f, 1.f); 73 mesh.vertices[13].pos = XMFLOAT3(halfW, halfH, -halfD); 74 mesh.vertices[13].normal = XMFLOAT3(1.f, 0.f, 0.f); 75 mesh.vertices[13].tangent = XMFLOAT3(0.f, 0.f, 1.f); 76 mesh.vertices[13].tex = XMFLOAT2(0.f, 0.f); 77 mesh.vertices[14].pos = XMFLOAT3(halfW, halfH, halfD); 78 mesh.vertices[14].normal = XMFLOAT3(1.f, 0.f, 0.f); 79 mesh.vertices[14].tangent = XMFLOAT3(0.f, 0.f, 1.f); 80 mesh.vertices[14].tex = XMFLOAT2(1.f, 0.f); 81 mesh.vertices[15].pos = XMFLOAT3(halfW, -halfH, halfD); 82 mesh.vertices[15].normal = XMFLOAT3(1.f, 0.f, 0.f); 83 mesh.vertices[15].tangent = XMFLOAT3(0.f, 0.f, 1.f); 84 mesh.vertices[15].tex = XMFLOAT2(1.f, 1.f); 85 //上面 86 mesh.vertices[16].pos = XMFLOAT3(-halfW, halfH, -halfD); 87 mesh.vertices[16].normal = XMFLOAT3(0.f, 1.f, 0.f); 88 mesh.vertices[16].tangent = XMFLOAT3(1.f, 0.f, 0.f); 89 mesh.vertices[16].tex = XMFLOAT2(0.f, 1.f); 90 mesh.vertices[17].pos = XMFLOAT3(-halfW, halfH, halfD); 91 mesh.vertices[17].normal = XMFLOAT3(0.f, 1.f, 0.f); 92 mesh.vertices[17].tangent = XMFLOAT3(1.f, 0.f, 0.f); 93 mesh.vertices[17].tex = XMFLOAT2(0.f, 0.f); 94 mesh.vertices[18].pos = XMFLOAT3(halfW, halfH, halfD); 95 mesh.vertices[18].normal = XMFLOAT3(0.f, 1.f, 0.f); 96 mesh.vertices[18].tangent = XMFLOAT3(1.f, 0.f, 0.f); 97 mesh.vertices[18].tex = XMFLOAT2(1.f, 0.f); 98 mesh.vertices[19].pos = XMFLOAT3(halfW, halfH, -halfD); 99 mesh.vertices[19].normal = XMFLOAT3(0.f, 1.f, 0.f); 100 mesh.vertices[19].tangent = XMFLOAT3(1.f, 0.f, 0.f); 101 mesh.vertices[19].tex = XMFLOAT2(1.f, 1.f); 102 //底面 103 mesh.vertices[20].pos = XMFLOAT3(-halfW, -halfH, halfD); 104 mesh.vertices[20].normal = XMFLOAT3(0.f, -1.f, 0.f); 105 mesh.vertices[20].tangent = XMFLOAT3(1.f, 0.f, 0.f); 106 mesh.vertices[20].tex = XMFLOAT2(0.f, 1.f); 107 mesh.vertices[21].pos = XMFLOAT3(-halfW, -halfH, -halfD); 108 mesh.vertices[21].normal = XMFLOAT3(0.f, -1.f, 0.f); 109 mesh.vertices[21].tangent = XMFLOAT3(1.f, 0.f, 0.f); 110 mesh.vertices[21].tex = XMFLOAT2(0.f, 0.f); 111 mesh.vertices[22].pos = XMFLOAT3(halfW, -halfH, -halfD); 112 mesh.vertices[22].normal = XMFLOAT3(0.f, -1.f, 0.f); 113 mesh.vertices[22].tangent = XMFLOAT3(1.f, 0.f, 0.f); 114 mesh.vertices[22].tex = XMFLOAT2(1.f, 0.f); 115 mesh.vertices[23].pos = XMFLOAT3(halfW, -halfH, halfD); 116 mesh.vertices[23].normal = XMFLOAT3(0.f, -1.f, 0.f); 117 mesh.vertices[23].tangent = XMFLOAT3(1.f, 0.f, 0.f); 118 mesh.vertices[23].tex = XMFLOAT2(1.f, 1.f); 119 120 //构建索引 121 mesh.indices[0] = 0; 122 mesh.indices[1] = 1; 123 mesh.indices[2] = 2; 124 mesh.indices[3] = 0; 125 mesh.indices[4] = 2; 126 mesh.indices[5] = 3; 127 128 mesh.indices[6] = 4; 129 mesh.indices[7] = 5; 130 mesh.indices[8] = 6; 131 mesh.indices[9] = 4; 132 mesh.indices[10] = 6; 133 mesh.indices[11] = 7; 134 135 mesh.indices[12] = 8; 136 mesh.indices[13] = 9; 137 mesh.indices[14] = 10; 138 mesh.indices[15] = 8; 139 mesh.indices[16] = 10; 140 mesh.indices[17] = 11; 141 142 mesh.indices[18] = 12; 143 mesh.indices[19] = 13; 144 mesh.indices[20] = 14; 145 mesh.indices[21] = 12; 146 mesh.indices[22] = 14; 147 mesh.indices[23] = 15; 148 149 mesh.indices[24] = 16; 150 mesh.indices[25] = 17; 151 mesh.indices[26] = 18; 152 mesh.indices[27] = 16; 153 mesh.indices[28] = 18; 154 mesh.indices[29] = 19; 155 156 mesh.indices[30] = 20; 157 mesh.indices[31] = 21; 158 mesh.indices[32] = 22; 159 mesh.indices[33] = 20; 160 mesh.indices[34] = 22; 161 mesh.indices[35] = 23; 162 }
为了构建一个圆柱,需要提供如下信息:圆柱的上口半径(topRadius),下口半径(bottomRadius),高度(height)。此外,为了指定圆柱的精细度,还需要指定两个参数,一个为没高度方向上平均划分的个数(stack),另一个为沿圆周方向等分的个数(slice)。
可以根据龙书中给出的图理解一下:
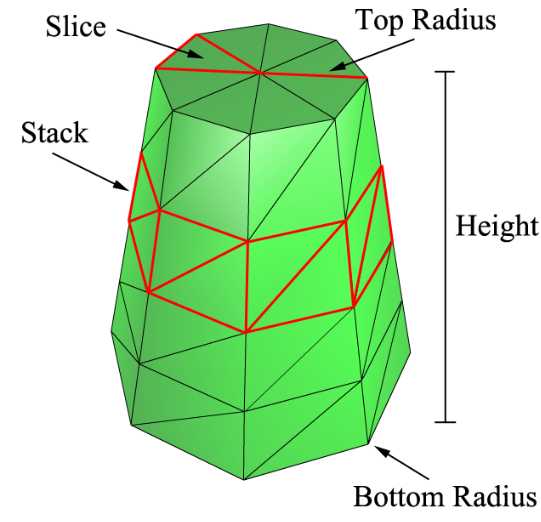
1 void GeometryGenerator::CreateCylinder(float topRadius, float bottomRadius, float height, int slice, int stack, MeshData &mesh) 2 { 3 mesh.vertices.clear(); 4 mesh.indices.clear(); 5 6 //从上到下每个stack半径变化量:dRadius 7 float dRadius = (bottomRadius - topRadius) / stack; 8 //每个stack高度:dHeight 9 float dHeight = height / stack; 10 11 //每个圆周上顶点数量:slice+1 12 int vertsPerRow = slice + 1; 13 //顶点行数:stack+1 14 int nRows = stack + 1; 15 16 //总顶点数 17 int nVerts = vertsPerRow * nRows; 18 //总索引数 19 int nIndices = slice * stack * 6; 20 21 mesh.vertices.resize(nVerts); 22 mesh.indices.resize(nIndices); 23 24 //顶部Y坐标 25 float topY = height * 0.5f; 26 27 for (int i = 0; i < nRows; ++i) 28 { 29 float tmpY = topY - dHeight * i; 30 float tmpRadius = topRadius + i * dRadius; 31 32 for (int j = 0; j < vertsPerRow; ++j) 33 { 34 float theta = XM_2PI * j / slice; 35 int index = i * vertsPerRow + j; 36 mesh.vertices[index].pos = XMFLOAT3(tmpRadius*cos(theta), tmpY, tmpRadius*sin(theta)); 37 } 38 } 39 40 UINT tmp(0); 41 for (int i = 0; i < stack; ++i) 42 { 43 for (int j = 0; j < slice; ++j) 44 { 45 mesh.indices[tmp] = i * vertsPerRow + j; 46 mesh.indices[tmp + 1] = (i + 1) * vertsPerRow + j + 1; 47 mesh.indices[tmp + 2] = (i + 1) * vertsPerRow + j; 48 mesh.indices[tmp + 3] = i * vertsPerRow + j; 49 mesh.indices[tmp + 4] = i * vertsPerRow + j + 1; 50 mesh.indices[tmp + 5] = (i + 1) * vertsPerRow + j + 1; 51 52 tmp += 6; 53 } 54 } 55 }
绘制球基本参数只有一个半径,但是同圆柱一样为了指定精细程度也要给出stack和slice两个参数,这里slice是从上极点沿球面到下极点的180度角等分。具体绘制可以看代码理解:
1 void GeometryGenerator::CreateSphere(float radius, int slice, int stack, MeshData &mesh) 2 { 3 4 mesh.vertices.clear(); 5 mesh.indices.clear(); 6 7 int vertsPerRow = slice + 1; 8 int nRows = stack - 1; 9 10 int nVerts = vertsPerRow * nRows + 2; 11 int nIndices = (nRows - 1)*slice * 6 + slice * 6; 12 13 mesh.vertices.resize(nVerts); 14 mesh.indices.resize(nIndices); 15 16 for (int i = 1; i <= nRows; ++i) 17 { 18 float phy = XM_PI * i / stack; 19 float tmpRadius = radius * sin(phy); 20 for (int j = 0; j < vertsPerRow; ++j) 21 { 22 float theta = XM_2PI * j / slice; 23 UINT index = (i - 1)*vertsPerRow + j; 24 25 float x = tmpRadius*cos(theta); 26 float y = radius*cos(phy); 27 float z = tmpRadius*sin(theta); 28 29 //位置坐标 30 mesh.vertices[index].pos = XMFLOAT3(x, y, z); 31 //法线 32 XMVECTOR N = XMVectorSet(x, y, z, 0.f); 33 XMStoreFloat3(&mesh.vertices[index].normal, XMVector3Normalize(N)); 34 //切线 35 XMVECTOR T = XMVectorSet(-sin(theta), 0.f, cos(theta), 0.f); 36 XMStoreFloat3(&mesh.vertices[index].tangent, XMVector3Normalize(T)); 37 //纹理坐标 38 mesh.vertices[index].tex = XMFLOAT2(j*1.f / slice, i*1.f / stack); 39 } 40 } 41 42 int size = vertsPerRow * nRows; 43 //添加顶部和底部两个顶点信息 44 mesh.vertices[size].pos = XMFLOAT3(0.f, radius, 0.f); 45 mesh.vertices[size].normal = XMFLOAT3(0.f, 1.f, 0.f); 46 mesh.vertices[size].tangent = XMFLOAT3(1.f, 0.f, 0.f); 47 mesh.vertices[size].tex = XMFLOAT2(0.f, 0.f); 48 49 mesh.vertices[size + 1].pos = XMFLOAT3(0.f, -radius, 0.f); 50 mesh.vertices[size + 1].normal = XMFLOAT3(0.f, -1.f, 0.f); 51 mesh.vertices[size + 1].tangent = XMFLOAT3(1.f, 0.f, 0.f); 52 mesh.vertices[size + 1].tex = XMFLOAT2(0.f, 1.f); 53 54 UINT tmp(0); 55 int start1 = 0; 56 int start2 = mesh.vertices.size() - vertsPerRow - 2; 57 int top = size; 58 int bottom = size + 1; 59 for (int i = 0; i < slice; ++i) 60 { 61 mesh.indices[tmp] = top; 62 mesh.indices[tmp + 1] = start1 + i + 1; 63 mesh.indices[tmp + 2] = start1 + i; 64 65 tmp += 3; 66 } 67 68 for (int i = 0; i < slice; ++i) 69 { 70 mesh.indices[tmp] = bottom; 71 mesh.indices[tmp + 1] = start2 + i; 72 mesh.indices[tmp + 2] = start2 + i + 1; 73 74 tmp += 3; 75 } 76 77 for (int i = 0; i < nRows - 1; ++i) 78 { 79 for (int j = 0; j < slice; ++j) 80 { 81 mesh.indices[tmp] = i * vertsPerRow + j; 82 mesh.indices[tmp + 1] = (i + 1) * vertsPerRow + j + 1; 83 mesh.indices[tmp + 2] = (i + 1) * vertsPerRow + j; 84 mesh.indices[tmp + 3] = i * vertsPerRow + j; 85 mesh.indices[tmp + 4] = i * vertsPerRow + j + 1; 86 mesh.indices[tmp + 5] = (i + 1) * vertsPerRow + j + 1; 87 88 tmp += 6; 89 } 90 } 91 }
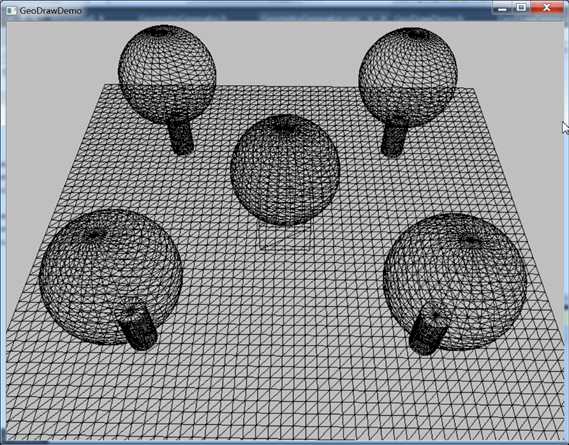
我们一共绘制了四种几何体:网格、立方体、球和圆柱,它们公用了一个顶点和索引缓冲区。这样我们就需要在其中找出每个几何体对应的位置。
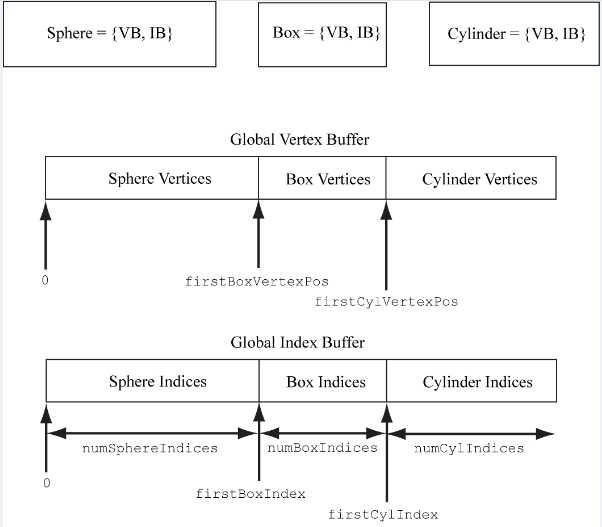
为了在顶点、索引缓冲区中找到一个物体对应的位置,我们使用三个参数:该物体在顶点缓冲区中的起始位置(VStart),索引缓冲区中的起始位置(IStart),以及索引总数(totalIndices)。看龙书中的一幅图就很容易理解了:
在Render函数中创建一个栅格化状态ID3D11RasterizerState ,状态描述中FillMode设为D3D11_FILL_WIREFRAME即可
1 //设置为线框绘制模式 2 D3D11_RASTERIZER_DESC rsDesc; 3 ZeroMemory(&rsDesc, sizeof(rsDesc)); 4 rsDesc.CullMode = D3D11_CULL_BACK; 5 rsDesc.DepthClipEnable = true; 6 //D3D11_FILL_WIREFRAME以线框模式绘制,D3D11_FILL_SOLID是以实体模式绘制 7 rsDesc.FillMode = D3D11_FILL_WIREFRAME; 8 rsDesc.FrontCounterClockwise = false; 9 ID3D11RasterizerState *rsState(nullptr); 10 m_pd3dDevice->CreateRasterizerState(&rsDesc, &rsState); 11 m_pImmediateContext->RSSetState(rsState);
由于具体代码太多就不一一给出了,代码和之前实现地形的代码类似,稍作改变就行啦。
标签:
原文地址:http://www.cnblogs.com/zhangbaochong/p/5573970.html