标签:
汽艇(Boat.cpp/c/pas)
【问题描述】
有 n 个人要去坐 1 汽艇,每个人单独坐汽艇的快乐程度是 Ci,每多一个人,他的快乐程度会减去 Di,请求出使快乐程度之和达到最大的方案。(假设汽艇的容量足够大)。
【输入格式】
输入文件共有 3 行:
第1 行是一个整数 n;
第2 行有n 个整数,依次表示每个人单独坐汽艇的快乐程度 Ci(1<=Ci<=10000);
第3 行有n 个整数,依次表示每多 1 人,每个人快乐程度的下降值 Di(1<=Di<=10)。
【输出格式】
应输出两行:
第1 行一个整数,是最大的快乐程度之和;
第2 行一个整数,是最大的快乐程度之和所对应的汽艇上的人数(若有多种方案,则输出人数最多的)。
【输入样例】
6
10 10 10 10 10 9
2 2 2 2 2 3
【输出样例】
18
3
【样例说明】
前 3 个人去坐汽艇可使快乐程度之和达到最大,每个人的快乐程度均为 10-2*2=6,总和是
18。
【数据范围】
对于 30%的数据,n<=20;
对于 100%的数据,n<=1000。
大水题,不多说,直接上代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout) 8 #define maxn 1010 9 10 using namespace std; 11 typedef long long llg; 12 13 int n,a[maxn],b[maxn]; 14 int v[maxn],ans,dd; 15 16 int getint(){ 17 int w=0,q=0; 18 char c=getchar(); 19 while((c<‘0‘||c>‘9‘)&&c!=‘-‘) c=getchar(); 20 if(c==‘-‘) q=1,c=getchar(); 21 while(c>=‘0‘&&c<=‘9‘) w=w*10+c-‘0‘,c=getchar(); 22 return q?-w:w; 23 } 24 25 int main(){ 26 File("boat"); 27 n=getint(); 28 for(int i=1;i<=n;i++) a[i]=getint(); 29 for(int i=1;i<=n;i++) b[i]=getint(); 30 for(int i=n,now;i;i--){ 31 now=0; 32 for(int j=1;j<=n;j++) v[j]=a[j]-(i-1)*b[j]; 33 sort(v+1,v+n+1); 34 for(int j=1;j<=i;j++) now+=v[n-j+1]; 35 if(now>ans) ans=now,dd=i; 36 } 37 printf("%d\n%d",ans,dd); 38 fclose(stdin);fclose(stdout); 39 return 0; 40 }
上网(net.cpp/c/pas)
【问题描述】
假设有 n 个人要上网,却只有 1 台电脑可以上网。上网的时间是从 1 szw 至 T szw ,szw是一个自创的时间单位,至于 szw怎么换算成 s,min 或 h,没有人清楚。依次给出每个人在某个时间段内上网的快乐程度 C(必须这个人在整个时间段内都在上网,才能获得快乐程度C,否则,快乐程度是 0),请你得到使总的快乐程度达到最大的方案。
【输入格式】
第1 行2 个整数 n和 T,含义如题目所述;
接下来有 n 个这样的结构(每两个相邻的结构之间有一空行,且第 1 个结构和第一行间有
一空行):
第1 行一个整数 Mi,表示第 i 个人的时间段的个数;
接下来有 Mi 行,每行3个整数 Xj,Yj,C,表示第 i个人在[Xj,Yj]内上网的快乐程度为 C,
因此有 Xj-Yj-1=1,X1=1,Ymi=T,Xj<=Yj。
【输出格式】
仅输出一行,为总的最大的快乐程度。
【输入样例】
3 10
3
1 3 6
4 7 9
8 10 3
3
1 3 5
4 7 10
8 10 1
4
1 3 2
4 8 2
9 9 6
10 10 3
【输出样例】
25
【样例说明】
在[1,3]内,安排 1 上网,快乐程度为 6;
在[4,7]内,安排 2 上网,快乐程度为 10; 在[8,8]内,不安排;
在[9,9]内,安排 3 上网,快乐程度为 6;
在[10,10]内,安排 3 上网,快乐程度为 3;
这是使总的快乐程度达到最大的方案,对应的值是 25。
【数据范围】
对于 30%的数据,n<=4,所有的 Mi<=5,T<=20;
对于 60%的数据,n<=100,所有的 Mi<=100,T<=2000;
对于 100%的数据,n<=500,所有的 Mi<=500,T<=500000,所有的 0<C<=10^9,并保证最终解 Max<=10^9。
又是一道水题,和codevs的线段覆盖简直一模一样。上代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout) 8 #define maxn 300010 9 10 using namespace std; 11 typedef long long llg; 12 13 struct data{ 14 int l,r,b; 15 bool operator < (const data &h)const{ 16 if(r==h.r) return l<h.l; 17 return r<h.r; 18 } 19 }s[maxn]; 20 int n,T,tn,f[maxn<<1]; 21 22 int getint(){ 23 int w=0,q=0; 24 char c=getchar(); 25 while((c<‘0‘||c>‘9‘)&&c!=‘-‘) c=getchar(); 26 if(c==‘-‘) q=1,c=getchar(); 27 while(c>=‘0‘&&c<=‘9‘) w=w*10+c-‘0‘,c=getchar(); 28 return q?-w:w; 29 } 30 31 int main(){ 32 File("net"); 33 n=getint();T=getint(); 34 for(int i=1,w;i<=n;i++){ 35 w=getint(); 36 while(w--){ 37 s[++tn].l=getint(); 38 s[tn].r=getint(); 39 s[tn].b=getint(); 40 } 41 } 42 sort(s+1,s+tn+1); 43 for(int i=1,now=1;i<=T;i++){ 44 f[i]=f[i-1]; 45 while(s[now].r==i && now<=tn){ 46 f[i]=max(f[i],f[s[now].l-1]+s[now].b); 47 now++; 48 } 49 } 50 printf("%d",f[T]); 51 fclose(stdin);fclose(stdout); 52 return 0; 53 }
集合(gather)
【问题描述】
小明总喜欢做一些与众不同的事情,最近他迷上了集合运算。他觉得光是简单的预算不过瘾,所以他把2个集合运算集合起来。由于小明很喜欢区间运算。于是他定义了一个这样的值。
你N个各不相同的区间,请你从中找出若干个区间使其权值最大。
W=|A1∪A2∪……∪AK|*|A1∩A2∩……AK|
其中{A1,A2……AK}(K>1,Ai<>Aj{i<>j})
如果这些区间没有交集则权值为0,给你N个各不相同的区间,请你从中找出若干个区间使其权值最大,并告诉小明。
【输入文件】
第一行N
接下来N行 l r(1<=l<r<=10^6)
【输出文件】
最大权值
【输入样例】
4
1 6
4 8
2 7
3 5
【输出样例】
24
【数据约定】
10% N<=10
30% N<=2*10^4
50% N<=10^5
100% 1<N<=10^6
这道题比较难,考场上没有想出来,只好打了个贪心骗分,搞到了20分。后来发现这道题其实是bzoj 2687 出题人真是懒。好吧,这也不能否认这的确是一道好题。这道题其实是决策单调优化dp(考试前我正在搞这个东西,但是没搞完,所以...)。
首先,我们发现两个区间肯定可以达到最优解。这是为什么呢?考虑一下当多个区间在一起时,他们的并是由两个区间提供的,而这两个区间的交肯定不会小于多个区间的交。所以最优解一定可以有两个区间得到。
其次,对于被包含的区间,我们只需找到一个包含它的区间算一下贡献即可(当这个区间被多个区间包含时这个区间的贡献肯定不如两个包含它的区间的优)。
然后,我们把剩下的区间按左端点排序(其实再算区间被包含时就需要将区间排序了)。这样我们就可以发现 若i区间的最优解为j,那么i后面的区间的最优解一定为j或在j的右边。
证明如下(来自bzoj2687: 交与并):
假设j<k,对于i,有:
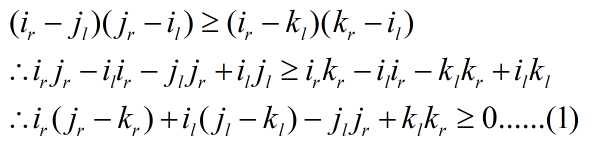
同理,对于i-1(记作i‘),有:
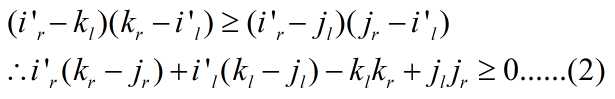
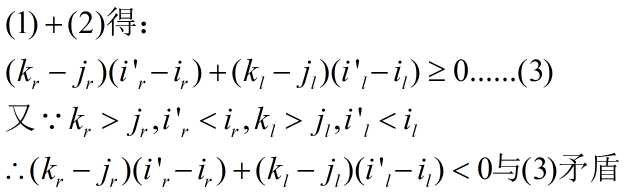
所以假设不成立,所以有k<=j。
所以我们就可以套用一下决策单调性的模板了(题解中O(n)单调栈的方法我并不会,我写的O(nlogn)的)。模板可参见bzoj 3156 防御准备。代码如下:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<algorithm> 6 #include<ctime> 7 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout) 8 #define maxn 1000010 9 #ifdef WIN32 10 #define OT "%I64d" 11 #else 12 #define OT "%lld" 13 #endif 14 15 using namespace std; 16 typedef long long llg; 17 18 struct data{ 19 int l,r; 20 bool operator < (const data &h)const{ 21 if(l==h.l) return r<h.r; 22 return l<h.l; 23 }; 24 }s[maxn]; 25 int n,zuo_,you_,; 26 int zl[maxn],zr[maxn],zx[maxn],lz,rz; 27 llg ans; 28 29 int getint(){ 30 int w=0,q=0; 31 char c=getchar(); 32 while((c<‘0‘||c>‘9‘)&&c!=‘-‘) c=getchar(); 33 if(c==‘-‘) q=1,c=getchar(); 34 while(c>=‘0‘&&c<=‘9‘) w=w*10+c-‘0‘,c=getchar(); 35 return q?-w:w; 36 } 37 38 llg jisuan(int x,int y){ 39 int l1=max(s[x].l,s[y].l),r1=min(s[x].r,s[y].r); 40 if(r1<=l1) return 0; 41 int l2=min(s[x].l,s[y].l),r2=max(s[x].r,s[y].r); 42 return (llg)(r1-l1)*(llg)(r2-l2); 43 } 44 45 int main(){ 46 File("gather"); 47 srand(time(NULL)); 48 n=getint(); 49 for(int i=1;i<=n;i++){ 50 s[i].l=getint(); 51 s[i].r=getint(); 52 } 53 sort(s+1,s+n+1); 54 zuo_=s[1].l;you_=s[1].r; 55 zl[rz]=2,zr[rz]=n,zx[rz++]=1; 56 for(int i=2,x;i<=n;i++){ 57 if(s[i].r<=you_){ //去掉被包含的区间并计算贡献 58 ans=max(ans,(llg)(you_-zuo_)*(s[i].r-s[i].l)); 59 continue; 60 } 61 you_=s[i].r;zuo_=s[i].l; 62 while(zr[lz]<i) lz++; //弹队首区间 63 ans=max(ans,jisuan(i,zx[lz])); 64 while(rz>lz){ 65 x=zl[rz-1]; 66 if(zl[rz-1]==i) x++; //这里注意一个区间不可以和自己算贡献,所以需要特判 67 if(jisuan(i,x)>=jisuan(zx[rz-1],x)) rz--; //弹队尾区间 68 else break; 69 } 70 if(rz==lz) zl[rz]=i+1,zr[rz]=n,zx[rz++]=i; 71 else{ 72 int l=zl[rz-1],r=zr[rz-1]+1,mid;x=zx[rz-1]; 73 if(i>=l && i<=r){ //一个区间不可以和自己算贡献,特判,把队尾区间拆成两个 74 if(jisuan(i,i+1)>=jisuan(x,i+1)){ //当右边的区间被弹掉之后,左边的区间也一定会被弹掉,所以直接弹掉并插入 75 zl[--rz]=i+1,zr[rz]=n,zx[rz++]=i; 76 continue; 77 } 78 else l=i+1; //在右边的区间中二分 79 } 80 while(l!=r){ 81 mid=l+r>>1; 82 if(jisuan(i,mid)>=jisuan(x,mid)) r=mid; 83 else l=mid+1; 84 } 85 zr[rz-1]=l-1; zl[rz]=l,zr[rz]=n,zx[rz]=i; 86 } 87 } 88 printf(OT,ans); 89 fclose(stdin);fclose(stdout); 90 return 0; 91 }
新斯诺克(snooker.cpp/c/pas)
【问题描述】
斯诺克又称英式台球,是一种流行的台球运动。在球桌上,台面四角以及两长边中心位置各有一个球洞,使用的球分别为 1 个白球,15 个红球和 6 个彩球(黄、绿、棕、蓝、粉红、黑)共22个球。击球顺序为一个红球、一个彩球直到红球全部落袋,然后以黄、绿、棕、蓝、粉红、黑的顺序逐个击球,最后以得分高者为胜。斯诺克的魅力还在于可以打防守球, 可以制造一些障碍球使对方无法击打目标球而被扣分。正是因为这样,斯诺克是一项充满神奇的运动。 现在考虑这样一种新斯诺克,设母球(母球即是白球,用于击打其他球)的标号为M,台面上有 N 个红球排成一排,每一个红球都有一个标号,`他们的标号代表了他们的分数。 现在用母球击打这些红球,一杆击打,如果母球接触到红球,就称为“K 到红球”。我们假设,一次可以击打任意多相邻连续的红球,也可以只击打一个球。并且红球既不会落袋,也不会相互发生碰撞,而只是停留在原处。每次击打时候,要想“K到红球”,至少要击打一个红球,如果想一次击打多个红球,那么击打的红球必须是依次连续排列的。 如果一次 “K 到红球”所有红球的标号之和的平均数大于母球的标号M,就获得了一个 “连击”。 现在请你计算总共能有多少种“连击”方案。
注意:如果当前有标号为 1、2、3的三种红球,母球标号为 0, 有如下 6 种获得“连击”方案: (1) 、 (2) 、 (3) 、 (1,2) 、 (2,3) 、 (1,2,3)
【输入文件】
输入文件共有两行,第一行是 N,M (N<=100000,M<=10000),
N 表示台面上一共有 N 个红球,M 表示母球的标号。
第二行是 N 个正整数,依次表示台面上 N 个红球的标号,所有标号均不超过10000。
【输出文件】
输出文件只有一个数,为“连击”的方案总数。
【输入样例】
4 3
3 7 2 4
【输出样例】
7
这道题又是原题,codevs上有 我都看不下去了。发现我们把每个数都减去m之后只需求出区间和大于0的个数。于是将原数组化为前缀和,求一下每个数前有多少个比他小的即可。
代码如下:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout) 8 #define maxn 100010 9 #ifdef WIN32 10 #define OT "%I64d" 11 #else 12 #define OT "%lld" 13 #endif 14 15 using namespace std; 16 typedef long long llg; 17 18 int n,m,w[maxn],c[maxn]; 19 llg ans; 20 21 int getint(){ 22 int w=0,q=0; 23 char c=getchar(); 24 while((c<‘0‘||c>‘9‘)&&c!=‘-‘) c=getchar(); 25 if(c==‘-‘) q=1,c=getchar(); 26 while(c>=‘0‘&&c<=‘9‘) w=w*10+c-‘0‘,c=getchar(); 27 return q?-w:w; 28 } 29 30 void qsort(int l,int r){ 31 if(l>=r) return; 32 int mid=l+r>>1,ll=l,rr=mid+1,k=l-1; 33 qsort(l,mid);qsort(mid+1,r); 34 while(ll<=mid && rr<=r){ 35 if(w[ll]<w[rr]) ans+=r-rr+1,c[++k]=w[ll++]; 36 else c[++k]=w[rr++]; 37 } 38 while(ll<=mid) c[++k]=w[ll++]; 39 while(rr<=r) c[++k]=w[rr++]; 40 for(int i=l;i<=r;i++) w[i]=c[i]; 41 } 42 43 int main(){ 44 File("snooker"); 45 n=getint();m=getint(); 46 for(int i=1;i<=n;i++) 47 w[i]=w[i-1]+getint()-m; 48 qsort(0,n); 49 printf(OT,ans); 50 fclose(stdin);fclose(stdout); 51 return 0; 52 }
标签:
原文地址:http://www.cnblogs.com/lcf-2000/p/5574249.html