标签:
1、两个栈实现一个队列,实现在队列尾部插入节点,在队列头部删除节点。
若为入队列则进stack1,若要出队列可分2种情况:a、若stack2为空,根据栈先进后出的特性应该先将stack1的元素pop出,进stack2。b、若 stack2不为空,可以说明stack2是前几次操作由stack1出栈的元素,符合队列先进先出的原则,则出队列操作可以直接使stack2中的栈顶元素出栈就可以了。如下图:
若有3个元素1,2,3依次入队列:
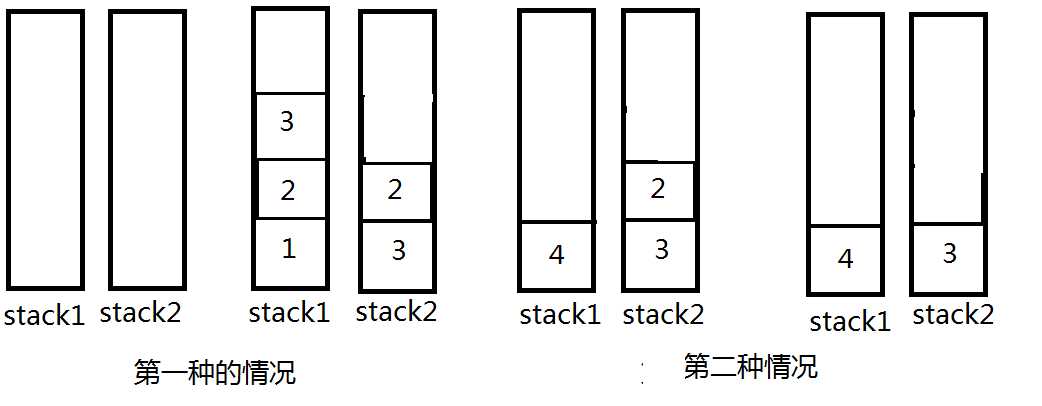
第一种情况:stack1和stack2都为空,入队列为进stack1,若要出队列,则将stack1中的元素依次出栈,push到 stack2 中,pop出stack2的栈顶元素则 为出队列.
第二种情况:此时stack2不为空若元素4要入队列则进stack1,若要出队列,此时stack2不为空则可以直接pop出栈顶元素2即可
代码如下:
#include<stack> template<class T> class Queue {public: Queue() {} ~Queue() {} void PushTail(const T&x) { stack1.push(x); } void PopHead() { if (stack2.size()<=0) { while (stack1.size() > 0) { T &a = stack1.top(); stack1.pop(); stack2.push(a); } } if (stack2.size() == 0) return; stack2.pop(); } private: stack<T> stack1; stack<T> stack2; };
2、两个队列实现一个栈
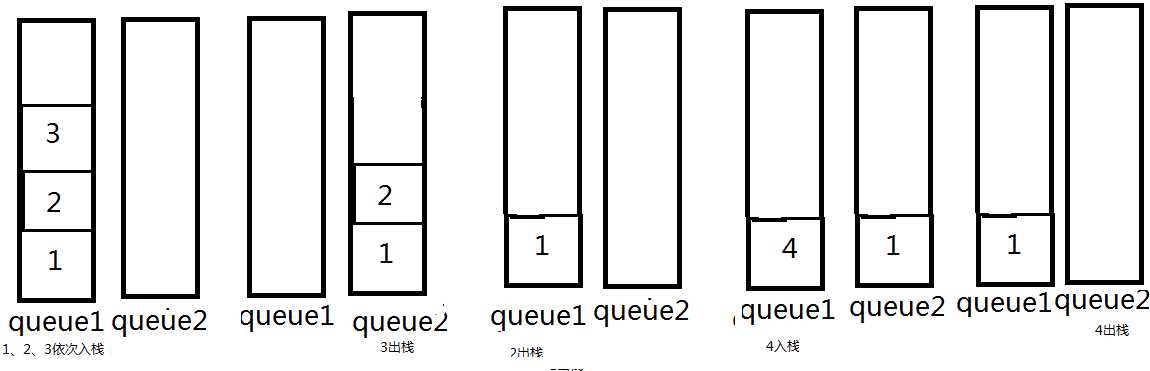
代码如下:
#include<queue> template<class T> class Stack { public: Stack() {} ~Stack() {} void PushHead(const T&x) { queue1.push(x); } void PopTail() { assert(queue1.size()>0 || queue2.size()>0) if (queue2.size() <= 0) { while (queue.size() > 0) { T &a = queue1.front(); queue1.pop(); queue2.push(a); } queue2.pop(); } if (queue1.size() <= 0) { while (queue2.size() > 0) { T &a = queue2.front(); queue2.pop(); queue1.push(a); }
queue1.pop();
}
}
private:
queue<T> queue1;
queue<T> queue2;
};
3、定义栈的数据结构,实现一个可以找到栈的最小元素的min函数,调用min、pop、push的时间复杂度为O(1);
分析:若每次新元素入栈时,排序让最小的元素在栈顶,这样可以实现min函数的时间复杂度为O(1),但一旦换了位置就不能满足栈先进后出的特点。
若在栈中设置一个变量,存放当前栈中最小元素,但是一旦最小元素pop出后则无法得到现在的最小元素。
可以设置一个辅助栈,每次数据入栈时,进入辅助栈的元素可以设置成(新入栈元素与以前入栈元素的最小值中的较小值)
代码如下:其中MinDate为存放数据的栈,Min为辅助栈
template<class T> void push(const T&x) {
MinDate.push(x); if (Min.size() == 0 || x < Min.top()) { Min.push(x) } else Min.push(Min.top()); } template<class T> void pop(const T&x) { assert(Min.size()>0 && MinData.size()>0) MinData.pop(); Min.pop(); } template<class T> T& min()const { assert(Min.size()>0 && MinData.size()>0) return Min.pop(); }
标签:
原文地址:http://www.cnblogs.com/Blog-day/p/MY_Blog_Days-9.html