标签:
第5章 回归模型:预测网页访问量
回归模型:用已知数据集预测另外一个数据集,已知数据集称为输入,也叫预测变量或特征,想要预测的数据称为输出。回归模型与分类模型的不同之处在于回归模型的输出是有意义的数值。
基准模型:用均值作为预测
#machine learing for heckers
#chapter 5
library(ggplot2) ages <- read.csv(‘ML_for_Hackers/05-Regression/data/longevity.csv‘) #密度图 ggplot(ages, aes(x = AgeAtDeath, fill = factor(Smokes))) + geom_density() + facet_grid(Smokes ~ .)
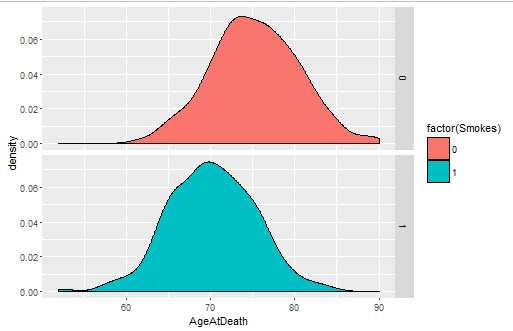
#采用均值作为估计时的均方误差与采用其他结果作为估计时的均方误差比较
guess <- 73
with(ages, mean((AgeAtDeath - guess) ^ 2))
guess.accuracy <- data.frame()
for(guess in seq(63, 83, by = 1)){
prediction.error <- with(ages, mean((AgeAtDeath - guess) ^ 2))
guess.accuracy <- rbind(guess.accuracy, data.frame(Guess = guess, Error = prediction.error))
}
ggplot(guess.accuracy, aes(x = Guess, y = Error)) + geom_point() + geom_line()

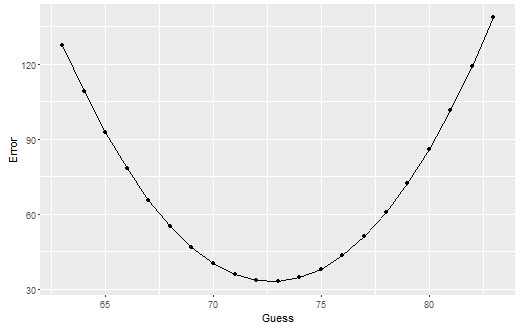
#对是否吸烟分组后,分别估计年龄均值,计算均方根误差
constant.guess <- with(ages, mean(AgeAtDeath)) with(ages, sqrt(mean((AgeAtDeath - constant.guess) ^ 2))) smokers.guess <- with(subset(ages, Smokes == 1), mean(AgeAtDeath)) non.smokers.guess <- with(subset(ages, Smokes == 0), mean(AgeAtDeath)) ages <- transform(ages, NewPrediction = ifelse(Smokes == 0, non.smokers.guess, smokers.guess)) with(ages, sqrt(mean((AgeAtDeath - NewPrediction) ^ 2)))
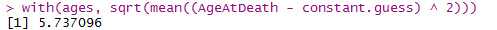

线性回归简介:
用到的假设:可加性;线性
一般性系统问题:回归擅长内推插值(interpolation),不擅长外推归纳(extrapolation). 也就是说,输入数据偏离观测数据太远,会造成预测不准确
模型如何才算有效?一个模型应该把真实世界的信号(预测值给出的)和噪声(残差给出的)区分开来,如果残差中除了真正的噪声外还存在信号,就说明模型没有强大到足以提取所有信号。
评价方法:
均方误差(MSE):可以评价预测的平均偏离,但是MSE是平均偏离值的平方
均方根误差(RMSE):MSE的开方值,但是不能让人直观清楚地看出模型不合理,即只能比较两个模型哪个更好,而不能单独评价一个模型的表现
R2:评价单独一个模型的好坏,以均值预测作为评估标准,值为0~1. 计算方式,分别计算以模型预测的RMSE1和均值预测的RMSE2,则R2 = 1-(RMSE1/RMSE2)
###################################
#预测网页流量
###################################
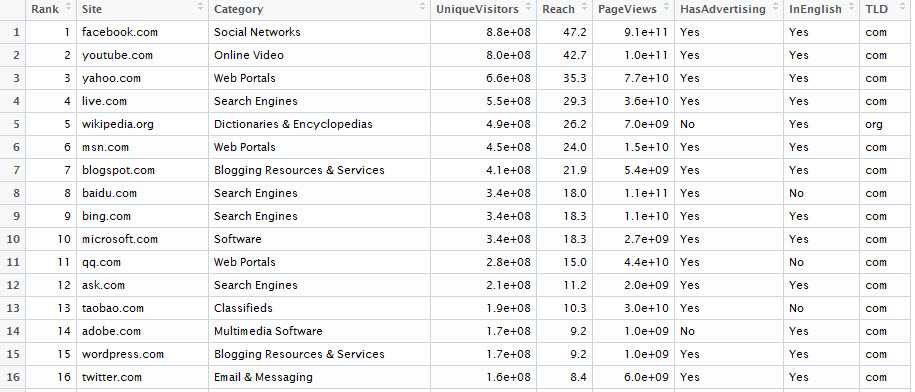
观察访问量和访问用户之间的关系,先绘制散点图和密度图
top.1000.sites <- read.csv(‘ML_for_Hackers/05-Regression/data/top_1000_sites.tsv‘, sep = ‘\t‘,
stringsAsFactors = FALSE)
ggplot(top.1000.sites, aes(x = PageViews, y = UniqueVisitors)) + geom_point()
ggplot(top.1000.sites, aes(x = PageViews)) + geom_density()
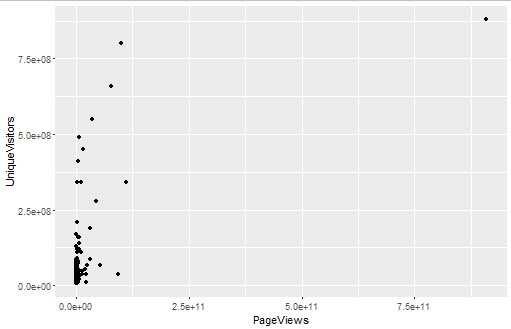
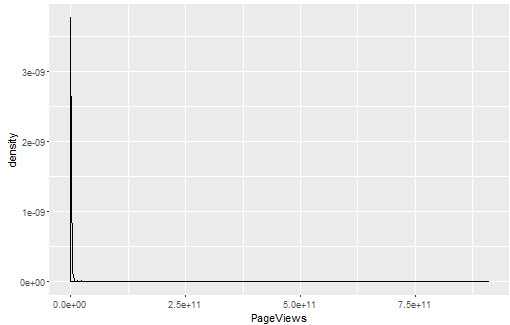
首先绘制的散点图都挤在了一起,所以考虑先看密度分布,但是密度分布也毫无意义,效果并不直观。这时要考虑先将数据对数变换,再绘制密度图和散点图。
ggplot(top.1000.sites, aes(x = log(PageViews))) + geom_density() ggplot(top.1000.sites, aes(x = log(PageViews), y = log(UniqueVisitors))) + geom_point() #也可以用ggplot2内置的scale_x_log10()和scale_y_log10()直接转换刻度,效果相同
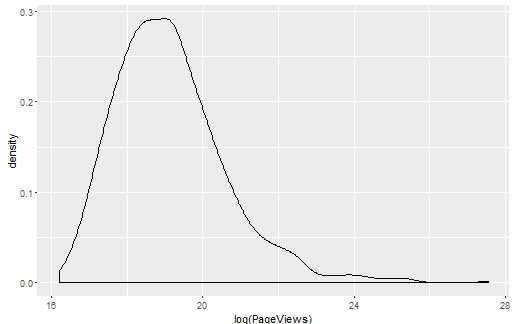
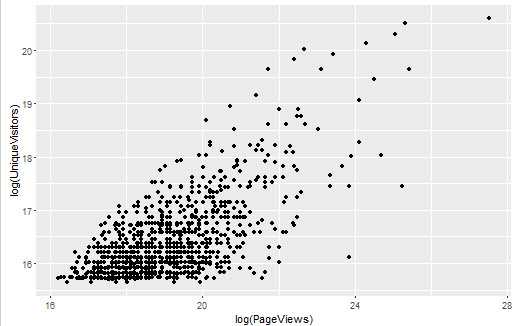
进行线性回归并解释结果:
lm.fit <- lm(log(PageViews) ~ log(UniqueVisitors), data = top.1000.sites) summary(lm.fit)
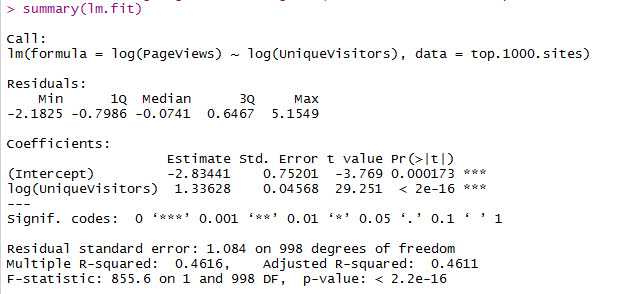
Call:调用函数
Risiduals:残差的分位数
Coefficients:回归模型的系数信息
Signif.codes:t-value有多大或者p-value有多小,t-value的意义就是系数估计值距离0的标准差个数,一般3个以上表示显著
Residual standard error:即RMSE。自由度:样本中独立或能自由变化的自变量的个数。由于已经确定了两个系数,而确定这两个系数至少需要2个自变量的值,因此该统计量的自由度是1000-2=998。自由度越大,RMSE越小,证明这个模型效果越好,越具有普遍性
Multiple R-squared:标准的R2值
Adjusted R-squared:根据使用的系数个数调整后的R2值,系数使用的越多,R2值得到的惩罚越大
F-statistic:表征了模型相对于仅使用均值预测所获得效果的提升度量,是R2的替代方案,可以用来计算p-value
(注:书中提到,p-value和F-statistic在模型预测问题上具有一定欺骗性,这两个指标更为合理的用法是用于拟合问题)
#########################################
#引入更多信息并进行回归
lm.fit <- lm(log(PageViews) ~ HasAdvertising + log(UniqueVisitors) + InEnglish, data = top.1000.sites) summary(lm.fit)
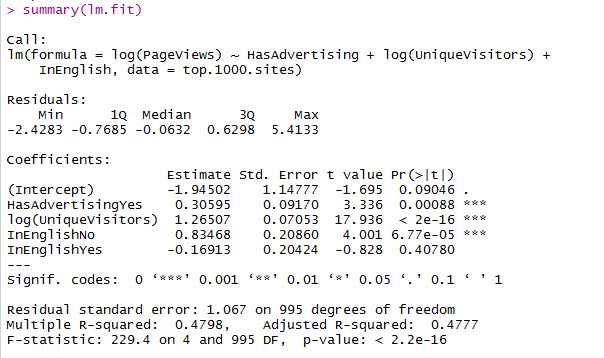
分析:
对于因子HasAdvertising:两种因子:‘YES‘和‘NO‘。 ‘YES‘从截距里分出来,‘NO‘包含在了截距(Intersept)中
对于因子InEnglish:三种因子:‘NA‘、‘YES‘和‘NO‘. ‘NA‘被包含在了截距里,‘YES‘和‘NO‘分别拟合系数
想要比较单独使用一个输入时,哪个输入具有更强的预测能力,可以提取每个summary函数的R2:
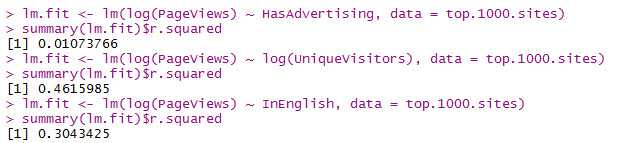
InEnglish应该解释了30%,应该是书上有误。这也解释了书上为什么提到1%的HasAdvertising可以舍去而不提3%的InEnglish
分析:因为HasAdvertising只解释了结果的1%,因此实践中,如果输入容易获得,值得将所有输入都包含进一个预测模型中,如果难以获得,可以从模型里去掉
#################################
相关性简述:
相关性可以衡量线性回归模型对两个变量之间关系建模的好坏:值为0时表明不存在直线能将两个变量联系起来;值为1时表明有一条完美正向直线可以将两个变量联系起来;值为-1时表明有一条完美的负向直线。
在R语言中,可以用函数cor()来计算相关性;
另一种计算方式是:用lm()函数对刻度变换后的两个变量进行拟合,得到的系数即是相关性。刻度变换方式是:先减去两个变量的均值,再除以标准差,在R语言中可以用scale()函数直接得到结果。
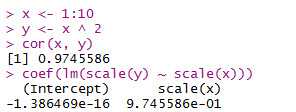
需要注意的是,相关性只能度量两个变量之间线性关系有多强,但是并不能说明两个变量之间是否有因果关系。而即使没有逻辑上的因果关系,对于预测问题来说,知道两个变量之间是否有相关性仍然十分重要。
标签:
原文地址:http://www.cnblogs.com/gyjerry/p/5576069.html