标签:
此处有目录↑
Codeforces Round #356(Div. 2):http://codeforces.com/contest/680
A little bear Limak plays a game. He has five cards. There is one number written on each card. Each number is a positive integer.
Limak can discard (throw out) some cards. His goal is to minimize the sum of numbers written on remaining (not discarded) cards.
He is allowed to at most once discard two or three cards with the same number. Of course, he won‘t discard cards if it‘s impossible to choose two or three cards with the same number.
Given five numbers written on cards, cay you find the minimum sum of numbers on remaining cards?
The only line of the input contains five integers t1, t2, t3, t4 and t5 (1?≤?ti?≤?100) — numbers written on cards.
Print the minimum possible sum of numbers written on remaining cards.
7 3 7 3 20
26
7 9 3 1 8
28
10 10 10 10 10
20
In the first sample, Limak has cards with numbers 7, 3, 7, 3 and 20. Limak can do one of the following.
You are asked to minimize the sum so the answer is 26.
In the second sample, it‘s impossible to find two or three cards with the same number. Hence, Limak does nothing and the sum is7?+?9?+?1?+?3?+?8?=?28.
In the third sample, all cards have the same number. It‘s optimal to discard any three cards. The sum of two remaining numbers is10?+?10?=?20.
题目大意:给定5张有数字的牌,可以去掉2张或3张数字相同的牌,使得剩余牌的数字和最小,求这个最小值?
非常水的题,但是还是坚持不枚举,想直接判断,结果写的时候不停地动摇自己想到的解法,导致第一题写了17min...
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int a[5],sum,cnt;
int main() {
while(scanf("%d%d%d%d%d",a,a+1,a+2,a+3,a+4)==5) {
sort(a,a+5);
sum=a[0]+a[1]+a[2]+a[3]+a[4];
if(a[0]==a[2]&&a[3]==a[4]) {//如果后两个一样且前三个一样(只有这种情况需要特判),则两者较大的
printf("%d\n",sum-max(a[0]+a[1]+a[2],a[3]+a[4]));
}
else {
cnt=1;
for(int i=3;i>=0;--i) {//从最大数开始的找到连续的2或3个,然后结束
if(a[i]==a[i+1]) {
if(cnt==3) {
sum-=cnt*a[i+1];
cnt=0;
break;
}
++cnt;
}
else {
if(cnt>1) {
sum-=cnt*a[i+1];
cnt=0;
break;
}
cnt=1;
}
}
if(cnt>1) {
sum-=cnt*a[0];
}
printf("%d\n",sum);
}
}
return 0;
}
There are n cities in Bearland, numbered 1 through n. Cities are arranged in one long row. The distance between cities i and j is equal to|i?-?j|.
Limak is a police officer. He lives in a city a. His job is to catch criminals. It‘s hard because he doesn‘t know in which cities criminals are. Though, he knows that there is at most one criminal in each city.
Limak is going to use a BCD (Bear Criminal Detector). The BCD will tell Limak how many criminals there are for every distance from a citya. After that, Limak can catch a criminal in each city for which he is sure that there must be a criminal.
You know in which cities criminals are. Count the number of criminals Limak will catch, after he uses the BCD.
The first line of the input contains two integers n and a (1?≤?a?≤?n?≤?100) — the number of cities and the index of city where Limak lives.
The second line contains n integers t1,?t2,?...,?tn (0?≤?ti?≤?1). There are ti criminals in the i-th city.
Print the number of criminals Limak will catch.
6 3 1 1 1 0 1 0
3
5 2 0 0 0 1 0
1
In the first sample, there are six cities and Limak lives in the third one (blue arrow below). Criminals are in cities marked red.
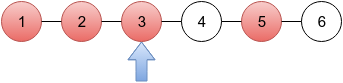
Using the BCD gives Limak the following information:
So, Limak will catch criminals in cities 1, 3 and 5, that is 3 criminals in total.
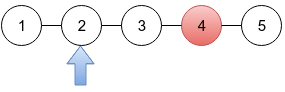
In the second sample (drawing below), the BCD gives Limak the information that there is one criminal at distance 2 from Limak‘s city. There is only one city at distance 2 so Limak is sure where a criminal is.
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,a,t,ans;
int cnt[105];
int main() {
while(scanf("%d%d",&n,&a)==2) {
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;++i) {
scanf("%d",&t);
if(t==1) {//统计与a点距离为abs(i-a)的罪犯数
++cnt[abs(i-a)];
}
}
ans=cnt[0];
for(int i=1;i<=n;++i) {//枚举距离
if(cnt[i]==2) {//如果罪犯数为2,则必定能分辨
ans+=2;
}
else if(cnt[i]==1&&(a-i<1||a+i>n)) {//如果罪犯数为1,且只有一个距离a为i的点,则也能分辨
++ans;
}
}
printf("%d\n",ans);
}
return 0;
}
This is an interactive problem. In the output section below you will see the information about flushing the output.
Bear Limak thinks of some hidden number — an integer from interval [2,?100]. Your task is to say if the hidden number is prime or composite.
Integer x?>?1 is called prime if it has exactly two distinct divisors, 1 and x. If integer x?>?1 is not prime, it‘s called composite.
You can ask up to 20 queries about divisors of the hidden number. In each query you should print an integer from interval [2,?100]. The system will answer "yes" if your integer is a divisor of the hidden number. Otherwise, the answer will be "no".
For example, if the hidden number is 14 then the system will answer "yes" only if you print 2, 7 or 14.
When you are done asking queries, print "prime" or "composite" and terminate your program.
You will get the Wrong Answer verdict if you ask more than 20 queries, or if you print an integer not from the range [2,?100]. Also, you will get the Wrong Answer verdict if the printed answer isn‘t correct.
You will get the Idleness Limit Exceeded verdict if you don‘t print anything (but you should) or if you forget about flushing the output (more info below).
After each query you should read one string from the input. It will be "yes" if the printed integer is a divisor of the hidden number, and "no" otherwise.
Up to 20 times you can ask a query — print an integer from interval [2,?100] in one line. You have to both print the end-of-line character and flush the output. After flushing you should read a response from the input.
In any moment you can print the answer "prime" or "composite" (without the quotes). After that, flush the output and terminate your program.
To flush you can use (just after printing an integer and end-of-line):
Hacking. To hack someone, as the input you should print the hidden number — one integer from the interval [2,?100]. Of course, his/her solution won‘t be able to read the hidden number from the input.
yes no yes
2 80 5 composite
no yes no no no
58 59 78 78 2 prime
The hidden number in the first query is 30. In a table below you can see a better form of the provided example of the communication process.

The hidden number is divisible by both 2 and 5. Thus, it must be composite. Note that it isn‘t necessary to know the exact value of the hidden number. In this test, the hidden number is 30.
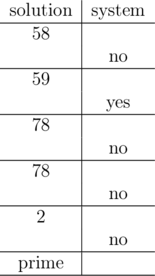
59 is a divisor of the hidden number. In the interval [2,?100] there is only one number with this divisor. The hidden number must be 59, which is prime. Note that the answer is known even after the second query and you could print it then and terminate. Though, it isn‘t forbidden to ask unnecessary queries (unless you exceed the limit of 20 queries).
题目大意:有一个[2,100]的数x,求x是素数还是合数?本题是一道交互式问题:这个数x没有告诉你,但是你可以至多询问20次进行判断,每次询问[2,100]内的一个数a,系统返回yes:代表a是x的因子;返回no:代表a不是x的因子。
第一次做这种类型的题,感觉好新颖
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int prime[15]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47};
int pre=1;
char cmd[5];
bool flag=false;
int main() {
for(int i=0,cnt=0;i<15&&cnt<20&&pre*prime[i]<=100;++i,++cnt) {
printf("%d\n",pre*prime[i]);
fflush(stdout);
scanf("%s",cmd);
if(cmd[0]=='y') {
if(flag) {
printf("composite\n");
fflush(stdout);
return 0;
}
else {
pre*=prime[i];
flag=true;
--i;//原来写的是i=-1;表示重新从2开始;改正后表示重新从prime[i]开始
}
}
}
printf("prime\n");
fflush(stdout);
return 0;
}
————————————————————3题的旅游分割线————————————————————Limak is a little polar bear. He plays by building towers from blocks. Every block is a cube with positive integer length of side. Limak has infinitely many blocks of each side length.
A block with side a has volume a3. A tower consisting of blocks with sides a1,?a2,?...,?ak has the total volume a13?+?a23?+?...?+?ak3.
Limak is going to build a tower. First, he asks you to tell him a positive integer X — the required total volume of the tower. Then, Limak adds new blocks greedily, one by one. Each time he adds the biggest block such that the total volume doesn‘t exceed X.
Limak asks you to choose X not greater than m. Also, he wants to maximize the number of blocks in the tower at the end (however, he still behaves greedily). Secondarily, he wants to maximize X.
Can you help Limak? Find the maximum number of blocks his tower can have and the maximum X?≤?m that results this number of blocks.
The only line of the input contains one integer m (1?≤?m?≤?1015), meaning that Limak wants you to choose X between 1 and m, inclusive.
Print two integers — the maximum number of blocks in the tower and the maximum required total volume X, resulting in the maximum number of blocks.
48
9 42
6
6 6
In the first sample test, there will be 9 blocks if you choose X?=?23 or X?=?42. Limak wants to maximize X secondarily so you should choose 42.
In more detail, after choosing X?=?42 the process of building a tower is:
So, there are 9 blocks in the tower. The total volume is is 33?+?23?+?7·13?=?27?+?8?+?7?=?42.
题目大意:有无限个边长为正整数的立方体,给定一个体积上限m,每次对于剩余体积X,选择最大的a使得a^3<=X成立的立方体,求选定一个体积X,使得使用的立方体的个数最多,满足个数最多同时尽量使X最大。
昨晚做的时候只能想到如何使个数最多,然后认为可以通过不断更改一个正方体的边长使得总体积变大,但是有点蒙,最后没写出来
今天看了题解发现可以枚举着贪心
对于当前上限limit,找到最大的a使得a^3<=limit成立,则当前可选立方体的边长为a和a-1
①当前选择边长为a的立方体,则新上限limit1=limit-a^3
②当前选择边长为a-1的立方体,则新上限limit2=(a^3-1)-(a-1)^3,【因为当体积大于等于a^3时,按照题意必定选择边长为a的立方体,所以选择边长为a-1的立方体时,体积只能选为a^3-1】
③当前选择边长为a-2的立方体,则新上限limit3=[(a-1)^3-1]-(a-2)^3
注意到对于上限limit来说,上限limit-1产生的结果不会更优,因为上限limit-1产生的结果更优的话,可以替换上限limit产生的结果
又:
limit2-limit3=(a^3-1)-(a-1)^3-{[(a-1)^3-1]-(a-2)^3}
=a^3+(a-2)^3-2*(a-1)^3
=(a+a-2)*[a^2-a*(a-2)+(a-2)^2]-2*(a-1)^3
=2*(a-1)*(a^2-2*a+4)-2*(a-1)^3
=2*(a-1)*[a^2-2*a+4-(a-1)^2]
=2*(a-1)*3
=6*(a-1)
所以limit2不小于limit3,即limit3产生的结果不会优于limit2产生的结果,则不再考虑边长为a-1以及更小的立方体
则问题转化为对于上限limit,取a和取a-1哪个结果更优?
对于这个问题,可以构造一个递归函数getCnt(limit);返回对于上限limit来说,最多能取多少个立方体
则当getCnt(limit)==getCnt(limit-cube(a))+1时,取a,否则取a-1
以下代码为参考code1写的,这种写法没有判断如何取,而是进行枚举找最大值
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int cnt;
long long m,ans;
long long cube(long long a) {
return a*a*a;
}
void dfs(long long limit,int depth,long long num) {
if(limit==0) {
if(cnt<depth) {
cnt=depth;
ans=num;
}
return ;
}
long long x=1;
while(cube(x+1)<=limit) {//找到最大能使x^3<=limit的值
++x;
}
dfs(limit-cube(x),depth+1,num+cube(x));//选择边长为x的立方体
if(x>1) {
dfs(cube(x)-1-cube(x-1),depth+1,num+cube(x-1));//不选边长为x的立方体,选择边长为x-1的立方体
}
}
int main() {
while(1==scanf("%I64d",&m)) {
cnt=0;
dfs(m,0,0);
printf("%d %I64d\n",cnt,ans);
}
return 0;
}
You have a grid with n rows and n columns. Each cell is either empty (denoted by ‘.‘) or blocked (denoted by ‘X‘).
Two empty cells are directly connected if they share a side. Two cells (r1,?c1) (located in the row r1 and column c1) and (r2,?c2) areconnected if there exists a sequence of empty cells that starts with (r1,?c1), finishes with (r2,?c2), and any two consecutive cells in this sequence are directly connected. A connected component is a set of empty cells such that any two cells in the component are connected, and there is no cell in this set that is connected to some cell not in this set.
Your friend Limak is a big grizzly bear. He is able to destroy any obstacles in some range. More precisely, you can choose a square of size k?×?k in the grid and Limak will transform all blocked cells there to empty ones. However, you can ask Limak to help only once.
The chosen square must be completely inside the grid. It‘s possible that Limak won‘t change anything because all cells are empty anyway.
You like big connected components. After Limak helps you, what is the maximum possible size of the biggest connected component in the grid?
The first line of the input contains two integers n and k (1?≤?k?≤?n?≤?500) — the size of the grid and Limak‘s range, respectively.
Each of the next n lines contains a string with n characters, denoting the i-th row of the grid. Each character is ‘.‘ or ‘X‘, denoting an empty cell or a blocked one, respectively.
Print the maximum possible size (the number of cells) of the biggest connected component, after using Limak‘s help.
5 2 ..XXX XX.XX X.XXX X...X XXXX.
10
5 3 ..... .XXX. .XXX. .XXX. .....
25
In the first sample, you can choose a square of size 2?×?2. It‘s optimal to choose a square in the red frame on the left drawing below. Then, you will get a connected component with 10 cells, marked blue in the right drawing.

题目大意:有一个n*n的土地,每一点有两种状态,‘X‘表示该点有障碍,‘.‘表示该点为平地,可以将一块k*k大小的土地夷为平地,即将其内的所有‘X‘变成‘.‘,而‘.‘则不变,求如此操作一次后,平地连通块的最大大小为多少?
比赛时只想到:先处理出所有的连通块及其大小,然后枚举k*k的土地的位置,然后统计与k*k土地相连的连通块的大小和,再加上k*k,还要减去在k*k土地内同时其连通块又在k*k土地外的点的个数,这样复杂度是O(n^2*k^2)
看完题解后,发现Sliding-window Technique这种方法可以利用已知的条件降低复杂度,因为每次只向右移动1,则只有正方形两边的2*k的点受到影响,其余的不变,所以每次移动时只用更改这2*k个点所带来的变化即可,每次往下移动时,初始化k*k正方形(共n-k次),则时间复杂度为(n*k^2),每次往右移动时,更改2*k个点所带来的变化(共(n-k)*(n-k)次),则时间复杂度为O(n^2*k),则枚举总时间复杂度为O(n*k^2+n^2*k)=O(n^2*k)
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN=505;
const int dr[4]={-1,0,1,0};
const int dc[4]={0,1,0,-1};
int n,k,cnt,ans,cur,time;
char g[MAXN][MAXN];
int color[MAXN][MAXN],num[MAXN*MAXN];
int addTime[MAXN*MAXN];
inline bool isInside(int r,int c) {
return 0<=r&&r<n&&0<=c&&c<n;
}
int dfs(int r,int c) {//dfs给同一连通块染色,并返回这一连通块的大小
int rr,cc,sze=1;
for(int i=0;i<4;++i) {
rr=r+dr[i];
cc=c+dc[i];
if(isInside(rr,cc)&&g[rr][cc]=='.'&&color[rr][cc]==0) {
color[rr][cc]=cnt;
sze+=dfs(rr,cc);
}
}
return sze;
}
void getConnectedComponent() {//搜索所有的连通块
memset(color,false,sizeof(color));
cnt=0;
for(int i=0;i<n;++i) {
for(int j=0;j<n;++j) {
if(g[i][j]=='.'&&color[i][j]==0) {
color[i][j]=++cnt;
num[color[i][j]]=dfs(i,j);
}
}
}
}
inline void addConnectedComponent(int r,int c) {//将(r,c)所在的连通块加入答案
if(isInside(r,c)&&g[r][c]=='.'&&addTime[color[r][c]]!=time) {//当(r,c)在范围内且(r,c)为空,且(r,c)所在的连通块本次还未加入答案时,才将其所在的连通块加入答案
addTime[color[r][c]]=time;
cur+=num[color[r][c]];
}
}
int main() {
while(2==scanf("%d%d",&n,&k)) {
for(int i=0;i<n;++i) {
scanf("%s",g[i]);
}
getConnectedComponent();
ans=0;
time=1;
memset(addTime,0,sizeof(addTime));//初始化所有的连通块均未加入答案
for(int r_sta=0;r_sta<=n-k;++r_sta) {//枚举正方形左上角的行坐标
for(int r=r_sta;r<r_sta+k;++r) {//初始化左上角为(r_sta,0)的正方形内连通块的大小
for(int c=0;c<k;++c) {
--num[color[r][c]];
}
}
for(int c_sta=0;c_sta<=n-k;++c_sta) {//枚举正方形左上角的列坐标
cur=k*k;
for(int r=r_sta;r<r_sta+k;++r) {//将正方形外左右两侧的连通块加入
addConnectedComponent(r,c_sta-1);
addConnectedComponent(r,c_sta+k);
}
for(int c=c_sta;c<c_sta+k;++c) {//将正方形外上下两侧的连通块加入
addConnectedComponent(r_sta-1,c);
addConnectedComponent(r_sta+k,c);
}
ans=max(ans,cur);
++time;
if(c_sta!=n-k) {//若正方形还能往右移动
for(int r=r_sta;r<r_sta+k;++r) {
++num[color[r][c_sta]];//正方形内左侧的连通块的大小+1
--num[color[r][c_sta+k]];//正方形外右侧的连通块的大小-1
}
}
}
for(int r=r_sta;r<r_sta+k;++r) {//当前行正方形枚举结束,还原左上角为(r_sta,n-k)的正方形内连通块的大小
for(int c=n-k;c<n;++c) {
++num[color[r][c]];
}
}
}
printf("%d\n",ans);
}
return 0;
}
Codeforces Round #356 (Div. 2) [Codeforces680]
标签:
原文地址:http://blog.csdn.net/idealism_xxm/article/details/51620094