标签:
英文原文请参考http://www.deeplearning.net/tutorial/logreg.html
这里,我们将使用Theano实现最基本的分类器:逻辑回归,以及学习数学表达式如何映射成Theano图。
逻辑回归是一个基于概率的线性分类器,W和b为参数。通过投射输入向量到一组超平面,每个对应一个类,输入到一个平面的距离反应它属于对应类的概率。
那么输入向量x为i类的概率,数值表示如下:
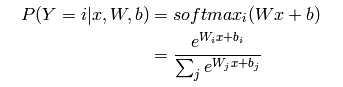
预测类别为概率最大的类,及:
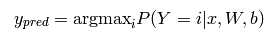
用Theano实现的代码如下:
# initialize with 0 the weights W as a matrix of shape (n_in, n_out) self.W = theano.shared( value=numpy.zeros( (n_in, n_out), dtype=theano.config.floatX ), name=‘W‘, borrow=True ) self.b = theano.shared( value=numpy.zeros( (n_out), dtype=theano.config.floatX ), name=‘b‘, borrow=True ) self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b) self.y_pred = T.argmax(self.p_y_given_x, axis=-1)
由于模型的参数在训练中维持一个持久的状态,因此我们将W,b设为共享变量,也是Theano符号变量。
目前定义的模型还没有做任何有用的事情,接下来将介绍如何学习最优参数。
对于多类回归,常见的是使用negative log-likelihood作为损失。
在参数θ下,最大化数据集D的似然函数,让我们先定义似然函数和损失:
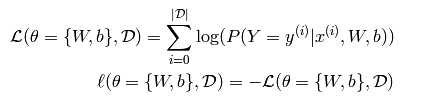
这里使用随机梯度下降的方法求最小值。
代码请参考源网址:http://www.deeplearning.net/tutorial/logreg.html
标签:
原文地址:http://www.cnblogs.com/liwei33/p/5578056.html