标签:
本文由量化、数据类型、上溢和下溢衍生,将浮点数看作是实数域的一种量化方式,分析浮点数,尤其是非规则浮点数和规则浮点数之间的差异。
为了更好理解本文内容,可先行阅读《量化、数据类型、上溢和下溢》中内容。这里依旧将浮点数看作是一种量化方式,将连续的不可数的集合映射到有限的集合上去。本文结合单精度浮点数讨论,双精度浮点与之类似。
已有多位博主撰写过关于非规则浮点数(Denormalized Number)和规则浮点数之间的区别,这里首推卢钧轶的你应该知道的浮点数基础知识。这篇文章从Denormal number和normal number之间的计算效率区别出发,概述了浮点数的相关知识,进而给出了Denormalized Number的定义,文中附有相应代码。浮点数的大部分知识可以从维基百科获取,包括
词条内容中的链接可以获取更多相关知识。
我在写量化、数据类型、上溢和下溢时有两个目的,一是从数字信号处理中量化的角度出发,阐明计算机内部数据的表示方式(即如何用有限的集合表示任意数,以及会带来什么样的问题),据此给出包括数据类型转化和计算过程中误差的产生原因;其二在于提醒自己无论是int或是double数据类型的数,表示能力都是有限的,在使用过程中需要注意上溢和下溢(尤其是下溢)的出现,以免出现错误。
在写的过程中,当我将浮点数当作非均匀量化时,却发现这个过程并不那么顺利,或许我应该单独的说明关于浮点数的相关内容,因此本文作为量化、数据类型、上溢和下溢的补充,旨在阐明
先给出一个示意图,这里将(0,4)区间非为了若干段,每段之间的数分配一个一样的值,这就是量化。而每段的长度是不同的,这种量化方式是非均匀的。
(By Blacklemon67 - created with tikz, CC BY-SA 3.0, https://en.wikipedia.org/w/index.php?curid=46487370)
为什么要进行非均匀量化?从数字信号处理的角度来说是为了保持相对一致的信噪比,当然可以简单的举个例子
测量1吨左右的物体,一般而言1吨零1克和零2克基本没有什么区别;然而测量重量约为1克的物体,是1克还是2克差别就很大了。
浮点数的具体定义在量化、数据类型、上溢和下溢中已经给出。
参考维基百科, 32比特浮点数的存储方式表示如下图。
对应浮点数取值可表示为(十进制) 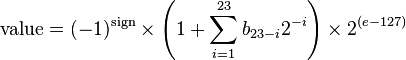
其中对于规则浮点数而言,指数项范围为01-FE(1到254)。大于0的浮点数依次为,然而大于1的浮点数依次为
,即量化间隔是不同的。指数项取FF时,可表示正负无穷或是非数(譬如0/0)。我们更关注的是,指数项取0时浮点数的特性。
先看看规则浮点数的特点,指数项定义了区间大小,下一段区间长度是当前段的2倍,而fraction将区间等间隔的划分为了段,如下图所示
显然,如果仅仅用规则浮点数的表示方式,0到最小正常数之间的间隔要远远大于最小正常数到次小正常数之间的间隔,这是不满足我们的期望的。因此选择规则浮点数指数项范围从1开始。剩下的一小段区间(即黄色括号)再均匀划分为段,此时指数项取0,表示方式为
通过这一手段,满足了当数据(绝对值)越小时,其量化间隔越小(或相等)的要求。这样可以一定程度上提高计算精度。譬如,若不引入非规则浮点数,任何小于的数将会下溢为0,而引入不规则浮点数后,小于
的数才会下溢为0 。
非规则浮点数的表示能力依旧是有限的,同时由于其与规则浮点数不相同的定义方式,会导致计算速率方面的问题,即
计算速率的问题在卢钧轶的你应该知道的浮点数基础知识中已有详细的讨论,这里不再重复,仅简单的说明原因,以加法为例,浮点数加/减的步骤为
非规则浮点计算加法时“对阶”计算有不同 。normal number和Denormal number的统一表示方式为
若A,B为Denormal number,对位过程中
也就是说对阶过程可能有三种结果,即,这增加了计算的复杂程度。但具体的计算过程我也不清楚,就写到这里了。
对于第二个问题,尽管非规则浮点数极大的提高了在0附近的精度,然而浮点数的精度依旧是有限的,无法阻止下溢的发生。因此在计算过程中,尤其是对精度要求较高以及算法是迭代的情况下,一定要注意下溢这一问题。对于溢出的讨论,可参见量化、数据类型、上溢和下溢。
标签:
原文地址:http://www.cnblogs.com/sea-wind/p/5568217.html