标签:
原文见链接:http://http//bubblexc.com/y2011/310/ 稍有修正。
直线、平面
在说超平面之前,先说说 Rn 空间中的直线和平面。给定 Rn 空间中的一点 p 和一非负向量 v? ,满足
i=tv? +p
的点 i 的集合称为 Rn 空间中的一条直线。上式中 t 是一个标量,向量 v? 决定了该直线的方向。如图1所示:
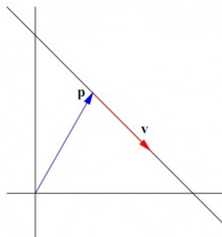
图1:line figure illustration
相对的,给定 Rn 空间中的一点 p和两个线性无关的向量 v? ,w? ,满足
i=tv? +sw? +p
的点 i 的集合称为 Rn 空间中的一个平面。上式中 t,s 均是标量。如图2所示:
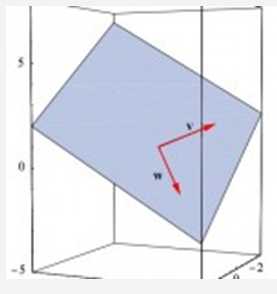
图2:plane figure illustration
更一般的,给定 Rn 空间中的一点 p和线性无关的向量 v1→,v2→,...,vk→,满足
i=t1v1→+t2v2→+...+tkvk→+p
的点 i 的集合称为 Rn 空间的一个k维仿射子空间(k-dimensional
affine subspace)。因此,一条直线就是一个1维仿射子空间,一个平面就是一个2维仿射子空间。
·
直线的另一种表示
假设 R2 空间中的点集 i=(x,y) 满足等式
ax+by+d=0 (1)
其中 a,b,d 均为标量,并且 a,b 至少有一个不为0。假设 b 不为0,则
y=−abx−db
设 x=t,−∞<t<∞,则点集i可以表示为
i=(x,y)=(t,−abt−db)=t(1,−ab)+(0,−db)
这其实是一条经过点 (0,−db) 方向为 (1,−ab) 的直线L。
进一步地,我们设 n? =(a,b),则(1)式可以表示为
n? ∗i+d=0 (2)
设取 p=(p1,p2) 为直线上一点,代入(2)式中的i,可以得到 d=−n? ∗p,则(2)式可以表示为
n? ∗(i−p)=0 (3)
可以看出,n? 实际是直线L的法向量,并且点集 i=(x,y) 是那些与 p 的差向量与 n? 正交的点。
·
超平面
说了这么多,现在来给出超平面的定义:给定 Rn 空间中的一点 p 和一个非零向量 n? 。满足
n? ∗(i−p)=0 (4)
的点集 i 称为经过点 p 的超平面。向量 n? 为该超平面的法向量。按照这个定义,一条直线是 R2 空间的超平面,一个平面是 R3 空间的超平面,Rn 空间的超平面是 Rn 空间
的一个n-1维仿射子空间。设 n? =(a1,a2,...,an),i=(i1,i2,...,in),则(4)式可以表示为
a1i1+a2i2+...+anin+d=0 (5)
其中,d=−n? ∗p
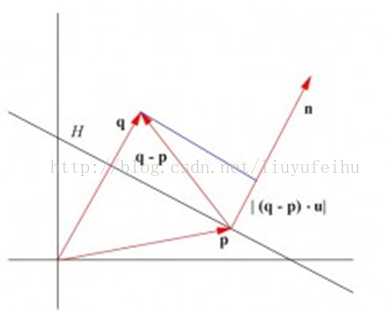
很重要的一点是,利用一个超平面,我们可以将空间的点分为两部分(式(4)的值大于等于0或者小于0)。同时,利用式(4)我们可以方面的计算空间内一点到超平面的距离:设空间中一点 q,q 到超平面的距离即是 q−p 在向量 n? 上的投影,如图(3)所示。q点距离超平面H的距离表示为:
d = |(q−p)∗u? |=|q∗n? −p∗n? | / ||n|| = |q∗n? +d| / ||n|| 其中u? 为n? 向量的单位向量,||n||为向量的模,代数上展开为L2范式
我们即可以求得 q 到超平面的距离。
标签:
原文地址:http://www.cnblogs.com/chyl411/p/5584801.html