标签:
概率论第三部分:二(多)维随机变量的性质计算
1.如何计算二维随机变量的联合分布函数?
思路:首先分类讨论:离散型:对分布律进行求和——连续型:求出概率密度函数,正确定限,积分。其中,正确定限是连续型求解中极其容易犯错的地方
例题:随机变量(x,y)服从d上的均匀分布,其中d为x轴、y轴及直线y=2x+1围成的三角形区域,求
(1)随机变量(x,y)的密度函数(2)随机变量(x,y)的分布函数
密度函数自然不用说,面积是1/4,所以密度函数一个是0,一个是4,(注意定义域:-1/2<=x<=0,0<=y<=2x+1)
重点来了,如何求解(x,y)的分布函数?
由定义可知:F(x,,y)=∫∫f(x,y)dxdy,(积分下限是-∞,上限分别是x和y)
但是我们要注意,f(x,y)仅在定义域(-1/2<=x<=0,0<=y<=2x+1)内是非零的,所以我们需要画图进行分类讨论。
- 由F(x)的定义 小于x的概率 ,我们就可以知道,当x和y有任意一个小于定义域的左边界时,从-∞积分上来都会因为f(x,y)==0而为0。
- 当x,y都在定义域的范围内时,我们可以认为x,y都是变量,所以x和y的积分上限都是x和y(因为在这种情况下,x和y是分别独立被给定的,之间没有关系),我们可以调换积分顺序,先积分的变量要用另外一个变量来确定上下限,本题中,如果先x后y,则x是:(-1/2*(y-1))——x,y是:0——y,如果先y后x,则x是:(-1/2)——x,而y是:2x+1——y
- 当x在定义域范围,而y出了定义域范围时,我们知道,y如果小于定义域中y的下限,则已经在1中讨论过为0,因此这里需要再讨论y大于定义域上限的情况。此时,由于y超出了范围,因此y不再是2中的那种“变量”,此时只有x可以被“给定”,所以此时要先积y,再积x,不能调换顺序,因为此时的F(x,y)需要用可以被给定的变量来刻画,也就是x。因此,积分上下限为,x是:-1/2——x,y是:0——2x+1,还是2x+1——1?答案是0——2x+1。为什么呢,因为这还是和F的含义有关,当x在定义域内,而y超出定义域时,我们通过画图,可以看出,给定一个x后,y的积分实际上还是从-∞到达一个超过了定义域的值为止,所以可以在图形上表示如下:所以,实际影响结果的还是涂黑的那部分。
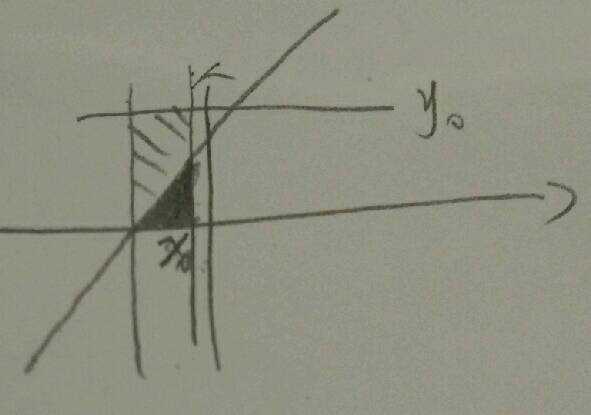
-
接下来,如果y在定义域内,而x超出了定义域,那么我们确定F(x,y)需要用y来表示,我们可以根据3中的思路,得到x和y的上下限:x为:(y-1)/2——0,y为:0——y
- 最后,如果x和y都超出了定义域,那么毫无疑问,F(x,y)==1
这样,我们就可以保证无遗漏地讨论了所有的F(x,y),只要求出并写出,就可以了。
概率论知识总结
标签:
原文地址:http://www.cnblogs.com/luruiyuan/p/5588283.html

