标签:
AC通道:http://www.lydsy.com/JudgeOnline/problem.php?id=3238

发现前面的len(Ti)+len(Tj)都是定值,所以其实我们的目标就是求出lcp(Ti,Tj)来.
lcp说实话就是一段子串对吧,但是不太好找.所以我们可以把串反过来.
这样的话,原图中后缀的最长公共前缀就变成了新串中前缀的最长公共后缀.
公共后缀是十分好求的,我们熟知parent边就是一个不断取后缀的过程,然后两者不断删去首字母,直到后缀相同的时候也就到了它们在parent树上的LCA的最长长度.
在一棵parent树上,考虑LCA可以是多少个点对的LCA.[应该是一个基本树型DP]
因为我们求的是前缀的公共后缀,所以每个状态只能取mx作为使用者.那么其实只要知道LCA的所有儿子的right集合大小即可.
right集合的每个位置分别表示了一段前缀[其实也就是这个节点下面的子树大小],然后与它父亲的其它可能的前缀的可能相乘 就得到了有多少个点对.
然后怎么求right集合的大小呢?
有一个性质就是parent树是一个right集合合并的过程,那么一个点的right集合大小就是其所有子树right集合大小之和.
还记得之前有画过一个图,现在再扯过来说一下:
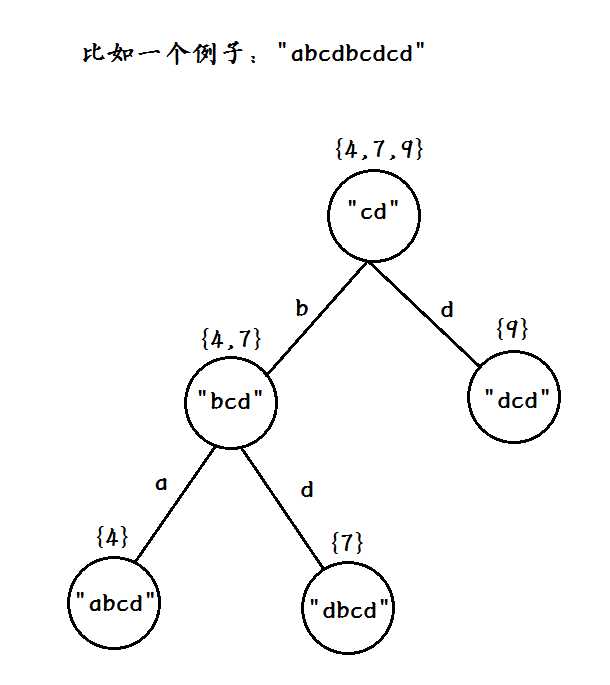
那么我们要是能把叶子节点的值赋值为1,然后沿着parent往上走就可以得到了.
叶子节点怎么找呢?其实很简单...当你每次extend的时候,你会增加一个新的节点np,这个节点中就只包含一个元素{n},然后其它所有right集合中有n的都是它的祖先,所以它就是一个叶子节点,需要+1.
而有时候我们将一个节点拆分成两个的时候,并没有产生新的元素,所以不是叶子节点不需要+1.
当然有时候你不确定的原因是有的,比如:"abab"中的"ab"它明明有儿子,但是它确实又是一个叶子节点,提供了它自己right集合里面的2这个元素.
("ab")={2,4}--b-->("bab")={4}
--无-->("无ab")={2}
所以每个前缀都一定在叶子节点上...好神奇啊...然后大家记住就好了.
当然还有一个拓扑序的完成,这个就是按照长度来弄一下顺序就好了,越长的当然越在后面.
看代码就好.

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1000010; int n,last=1,cnt=1; int a[maxn][26],mx[maxn],fa[maxn]; int T[maxn],Seq[maxn]; int f[maxn],w[maxn]; char ch[maxn]; void extend(int c){ int p=last,np=last=++cnt; mx[np]=mx[p]+1; f[np]=w[np]=1; while(!a[p][c] && p) a[p][c]=np,p=fa[p]; if(!p) fa[np]=1; else{ int q=a[p][c]; if(mx[q]==mx[p]+1) fa[np]=q; else{ int nq=++cnt;mx[nq]=mx[p]+1; memcpy(a[nq],a[q],sizeof(a[q])); fa[nq]=fa[q]; fa[q]=fa[np]=nq; while(a[p][c]==q) a[p][c]=nq,p=fa[p]; } } } void get_order(){ for(int i=1;i<=cnt;i++) T[mx[i]]++; for(int i=1;i<=n;i++) T[i]+=T[i-1]; for(int i=1;i<=cnt;i++) Seq[T[mx[i]]--]=i; } ll solve(){ ll ans=0; for(int i=cnt;i>=1;i--) f[fa[Seq[i]]]+=f[Seq[i]]; for(int i=cnt;i>=1;i--){ int x=Seq[i]; ans+=(ll)f[x]*w[fa[x]]*mx[fa[x]]; w[fa[x]]+=f[x]; } return ans; } int main(){ #ifndef ONLINE_JUDGE freopen("3238.in","r",stdin); freopen("3238.out","w",stdout); #endif scanf("%s",ch); n=strlen(ch); for(int i=n-1;i>=0;i--) extend(ch[i]-‘a‘); ll ans=(ll)(1+n)*n*(n-1)/2; get_order(); ans-=solve()*2; printf("%lld",ans); return 0; }
标签:
原文地址:http://www.cnblogs.com/Robert-Yuan/p/5591627.html