标签：
数制转换
十进制：有10个基数：0,1,2,3,4,5,6,7,8,9
二进制：有 2 个基数：0,1
八进制：有 8 个基数：0,1,2,3,4,5,6,7
十六进制：有16个基数：0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F （A=10，B=11，C=12，D=13，E=14，F=15）
十进制与其他进制之间的转换
一、（1）十进制——二进制：十进制数除以2，除至0时所得余数按反方向写出，即为二进制数。
例：
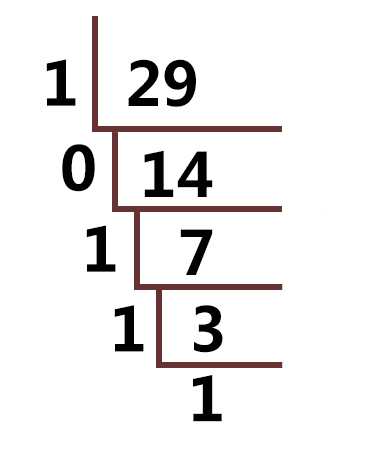所得出的二进制为：11101（2）[商为偶数时余数为0；奇数时余数为1]
（2）二进制——十进制
计算公式：ax20+bx21+cx22+...+mx2（n-1）=
a表示二进制右边的第一位数，b表示二进制右边的第二位数...m表示二进制右边的第（n-1）位数。
例：1011001
1x20+0x21+1x22+1x23+0x24+0x25+1x26
=1+8+16+64
=89
| 二进制右数位数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 十进制数 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
| 公式原型 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
二、（1）十进制——八进制：十进制数逐次整除8，直至商为0，所得余数按照相反的顺序写出，即为八进制。
例：139写成八进制为213（8）
（2）八进制——十进制
计算公式：ax80+bx81+cx82+...+mx8（n-1）=
原理同二进制
| 从右第n位 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 8（n-1） | 87 | 86 | 85 | 84 | 83 | 82 | 81 | 80 |
| 十进制下的实际数 | 2097152 | 262144 | 32768 | 4096 | 512 | 64 | 8 |
1 |
三、（1）十进制——十六进制
原理同二进制
（2）十六进制——十进制
原理同二进制
| 163 | 162 | 161 | 160 |
| 4096 | 256 | 16 | 1 |
其他进制之间的转换
二进制转换为八进制：对于整数，采用从右到左每三位一组，不够三位的在其左边补齐0，每组单独转换出来（右往左），即为八进制数。
例：
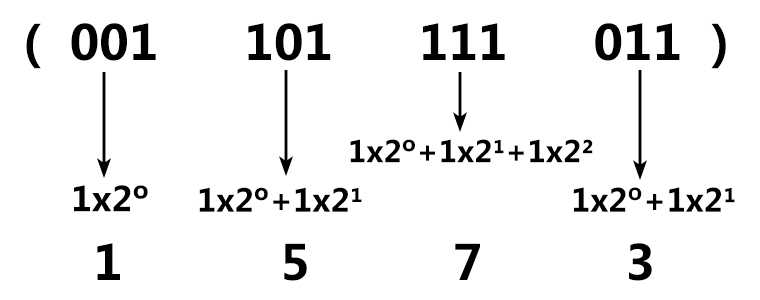
八进制转换为二进制：将每位八进制由三位二进制数代替。（不够三位前面补零）
例：（ 1 7 3 5 ）
001 111 011 101
所以，（1111011101）为所得的二进制数
二进制转换为十六进制：由于2的4次方=16，同二转八方法，将二进制数的每四位用一个十六进制的数码来表示，整数部分以小数点为界点从右往左每四位一组转换，
小数部分从小数点开始自左向右每四位一组进行转换。
例：（ 1001 0111 0111 1001 ）
9 7 7 9
十六进制转换为二进制： 只要将每一位十六进制数用四位相应的二进制数表示，即可完成转换。
例：（ 8 7 6 5 ）
1000 0111 0110 0101
所以，（1000 0111 0110 0101）为所得的二进制数
标签：
原文地址：http://www.cnblogs.com/ShenG1/p/5594579.html
