图论小王子小C经常虐菜,特别是在图论方面,经常把小D虐得很惨很惨。
这不,小C让小D去求一个无向图的最大独立集,通俗地讲就是:在无向图中选出若干个点,这些点互相没有边连接,并使取出的点尽量多。
小D虽然图论很弱,但是也知道无向图最大独立集是npc,但是小C很仁慈的给了一个很有特点的图: 图中任何一条边属于且仅属于一个简单环,图中没有重边和自环。小C说这样就会比较水了。
小D觉得这个题目很有趣,就交给你了,相信你一定可以解出来的。
标签:
作为切SDOI2010Area的铺垫
仙人掌DP求 最大独立集
最大独立集:感性的描述就是,一个图中,相邻点不能同时选,选出来最(多/点权总和最大)的点集
对于一般图,往往采用 转化成补图 求 最大团
但基于 树 和 仙人掌 可以利用DP求解 (树形DP求最大独立集,详见 CodeVS1380没有上司的舞会)
至于仙人掌,就是树+基环,且强连通(描述简陋,垃圾),详见下:
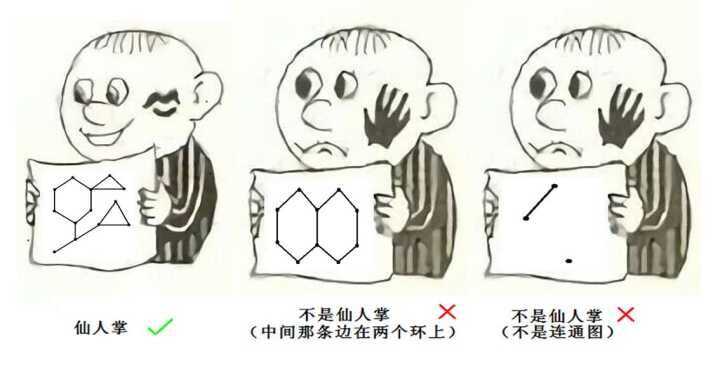
仙人掌DP的话,与树形DP同理,对于树边,可以直接进行树形DP,对于环,考虑单独处理,即单独DP,DP方式和树形DP一样
dp[x][0/1]表示 (选/不选)X节点的最优答案
转移显而易见,至于对环的考虑方法,可以采用Tarjan求强连通分量的思路,利用low和dfn进行判断 更多详见 某论文
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int read() { int x=0,f=1; char ch=getchar(); while (ch<‘0‘ || ch>‘9‘) {if (ch==‘-‘) f=-1; ch=getchar();} while (ch>=‘0‘ && ch<=‘9‘) {x=x*10+ch-‘0‘; ch=getchar();} return x*f; } #define maxn 100010 struct EdgeNode{int next,to;}edge[maxn<<2]; int head[maxn],cnt; void add(int u,int v) {cnt++; edge[cnt].next=head[u]; head[u]=cnt; edge[cnt].to=v;} void insert(int u,int v) {add(u,v); add(v,u);} int n,m,ans,tot; int dp1[maxn][2],dp2[maxn][2],ring[maxn],fa[maxn],dfn[maxn],low[maxn],t,deep[maxn]; void CactusDP(int st,int tt) { ring[0]=st; ring[1]=tt; int zz=1; while (ring[zz]!=st) {ring[zz+1]=fa[ring[zz]]; zz++;} dp2[0][0]=dp2[0][1]=0; for (int i=1; i<=zz; i++) dp2[i][1]=dp2[i-1][0]+dp1[ring[i]][1], dp2[i][0]=max(dp2[i-1][0],dp2[i-1][1])+dp1[ring[i]][0]; int tmp=dp2[zz][0]; dp2[0][0]=-0x7fffffff; for (int i=1; i<=zz; i++) dp2[i][1]=dp2[i-1][0]+dp1[ring[i]][1], dp2[i][0]=max(dp2[i-1][0],dp2[i-1][1])+dp1[ring[i]][0]; dp1[st][0]=tmp; dp1[st][1]=dp2[zz][1]; } void TreeDP(int now) { dfn[now]=low[now]=++t; dp1[now][1]=1; dp1[now][0]=0; for (int i=head[now]; i; i=edge[i].next) if (edge[i].to!=fa[now]) { if (deep[edge[i].to]) {low[now]=min(dfn[edge[i].to],low[now]); continue;} fa[edge[i].to]=now; deep[edge[i].to]=deep[now]+1; TreeDP(edge[i].to); if (low[edge[i].to]>dfn[now]) dp1[now][1]+=dp1[edge[i].to][0],dp1[now][0]+=max(dp1[edge[i].to][1],dp1[edge[i].to][0]); low[now]=min(low[now],low[edge[i].to]); } for (int i=head[now]; i; i=edge[i].next) if (edge[i].to!=fa[now] && low[edge[i].to]==dfn[now] && deep[edge[i].to]!=deep[now]+1) CactusDP(now,edge[i].to); } int main() { n=read(),m=read(); for (int u,v,i=1; i<=m; i++) u=read(),v=read(),insert(u,v); for (int i=1; i<=n; i++) if (!dfn[i]) {deep[i]=1; fa[i]=i; TreeDP(i); ans+=max(dp1[i][0],dp1[i][1]);}//为了防止出现仙人掌森林的情况QAQ printf("%d\n",ans); return 0; }
【BZOJ-4316】小C的独立集 仙人掌DP + 最大独立集
标签:
原文地址:http://www.cnblogs.com/DaD3zZ-Beyonder/p/5595119.html