标签:
本文将使用非常理想化的模型粗略地计算白昼时间和正午时刻,并以此算出日出、日没的时间。
怎么算白昼时间?或者说,怎么算白昼时间占一天时间中的比例?算出太阳的周日平行圈(太阳在天球上运动的轨迹)有多大一部分在地平线以上就可以了(忽略太阳一天之内的公转以及地球自转的不均匀)。
想要算出这个比例,需要这两个量:
| 符号 | 含义 | Why? |
| \( \delta \) | 太阳赤纬(太阳直射点纬度,北纬为正) | 夏天昼长,冬天昼短 |
| \( \varphi \) | 当地纬度(北纬为正) | 北极极昼,南极极夜 |
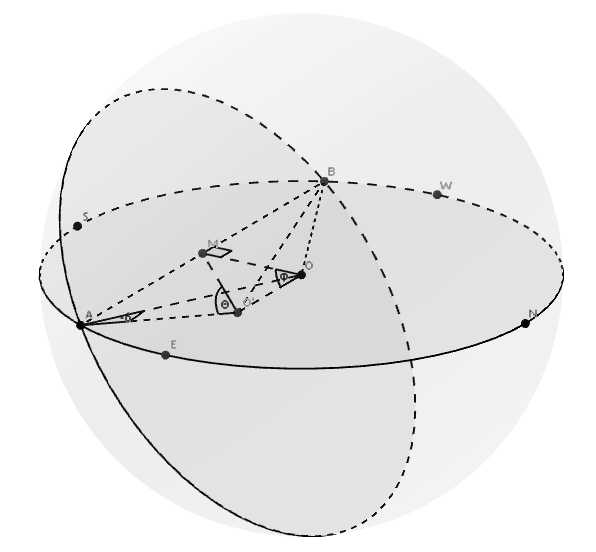
如图,以北半球冬季为例,把天球、地平线和平行圈画出来,再作几条辅助线,通过几何关系来用 \( \delta \) 和 \( \varphi \) 表示要求的比例:
设天球的球心为 \(O\), 半径为 \(1\), 平行圈的圆心为 \(O‘\), 太阳从 \(A\) 点升起,从 \(B\) 点落下,观察者不在极点。连接 \(AB\), \(AO\), \(AO‘\), \(BO\), \(BO‘\).
取 \(AB\) 的中点 \(M\), 连接 \(MO\), \(MO‘\). 易知 \( \angle{OAO‘} = -\delta \), \( \angle{MOO‘} = \varphi \).
设 \( \angle{MO‘A} = \theta \), 则所求比例为 \( \frac{2\theta}{360^{\circ}} = \frac{\theta}{180^{\circ}} \).
\( \because OO‘\perp 平面 O‘AB \)
\( \therefore OO‘\perp O‘M, OO‘\perp O‘A \)
\( \therefore O‘O = \sin{(-\delta)}, O‘A = \cos{(-\delta)} \)
\( \therefore O‘M = O‘O \cdot \tan{\varphi} = \sin{(-\delta)}\tan{\varphi} \)
\( \therefore \cos{\theta} = \frac{O‘M}{O‘A} = \frac{\sin{(-\delta)}\tan{\varphi}}{\cos{(-\delta)}} = \tan{(-\delta)}\tan{\varphi} \)
\( \therefore \theta = \arccos{(\tan{(-\delta)}\tan{\varphi})} \)
\( \therefore \frac{\theta}{{180}^{\circ}} = \frac{\arccos{(\tan{(-\delta)}\tan{\varphi})}}{{180}^{\circ}} \)
得到昼长关于 \( \delta \) 和 \( \varphi \) 的表达式:
\( \mathrm{daytime} = \frac{\arccos{(\tan{(-\delta)}\tan{\varphi})}}{{180}^{\circ}} \cdot {24}^{\mathrm{h}} \) \( (\varphi \neq \pm {90}^{\circ}) \)
虽然这个式子是从「北半球冬季」这一种情况推出来的,但也适用于南半球和夏季(代入 \( -\delta \) 和 \( -\varphi \) 容易看出)。
……
那么问题来了:\( \delta \) 怎么求?还得画个球:
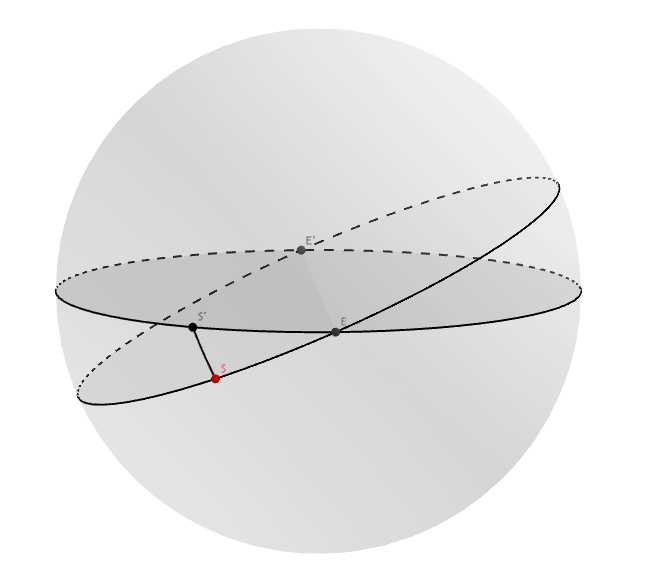
如图,天球的中心是地球,黄道和赤道相交,设春分点为 \(E\), 秋分点为 \(E‘\), 太阳为 \(S\), 黄赤交角为 \( \varepsilon \), 太阳地心黄经为 \( \lambda \).
通过几何关系用 \( \varepsilon \) 和 \( \lambda \) 表示 \( \delta \):
过 \(S\) 作大圆弧 \(SS‘\) 垂直于赤道交赤道于 \(S‘\) ( 图示位罝 ).
跟据球面三角形正弦定理,在球面 \( \triangle{SES‘} \) 中,有:
\( \frac{\sin{(-\delta)}}{\sin{\varepsilon}}=\frac{\sin{(-\lambda)}}{\sin{{90}^{\circ}}} \)
\( \sin{\delta} = \sin{\lambda}\sin{\varepsilon} \)
\( \delta = \arcsin{(\sin{\lambda}\sin{\varepsilon})} \)
这个式子也是适用于各种情况的。
……
问题又来了,\( \lambda \) 怎么求?这就不用画球了,也没球可画了。一是可以直接用轨道参数去算,二是可以先搞到各节气的日期,然后在邻近的两个节气间进行线性插值。
联立以上各式,可得白昼时间关于纬度和太阳黄经的表达式:
\( \mathrm{daytime} = {24}^{\mathrm{h}}\cdot\frac{\arccos{(\tan{(-\arcsin{(sin{\lambda}sin{\varepsilon})})}\tan{\varphi})}}{{180}^{\circ}} \) \( (\varphi \neq \pm {90}^{\circ}) \)
或
\( \mathrm{daytime} = {24}^{\mathrm{h}}\cdot(1-\frac{\arccos{(\tan{(\arcsin{(sin{\lambda}sin{\varepsilon})})}\tan{\varphi})}}{{180}^{\circ}}) \) \( (\varphi \neq \pm {90}^{\circ}) \)
或
\( \mathrm{daytime} = {24}^{\mathrm{h}}\cdot(1-\frac{\arccos{\frac{\sin{\lambda}\sin{\varepsilon}\tan{\varphi}}{\sqrt{1-\sin^2{\lambda}\sin^2{\varepsilon}}}}}{{180}^{\circ}}) \) \( (\varphi \neq \pm {90}^{\circ}) \)
北纬 \( {36.5}^{\circ} \) 的白昼时间关于太阳黄经的变化情况如下图:
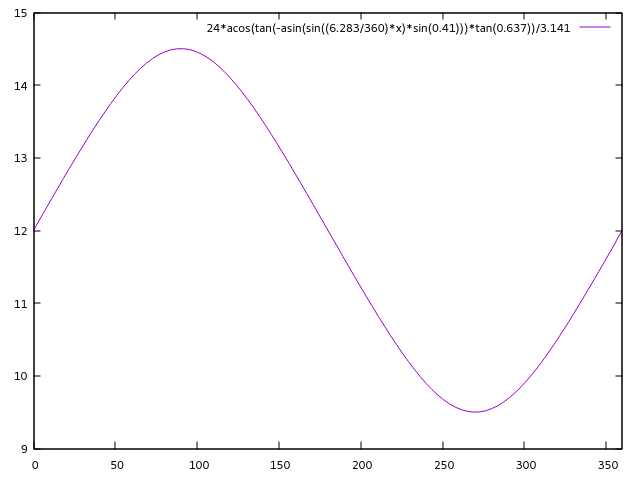
看起来特别像正弦曲线,尝试拟合一下:
\( \mathrm{daytime} \approx {12}^{\mathrm{h}} \cdot [(1-\frac{\arccos{(\tan{\varepsilon}\tan{\varphi})}}{{90}^{\circ}})\cdot sin{\lambda} + 1] \) \( (\varphi \neq \pm {90}^{\circ}) \)
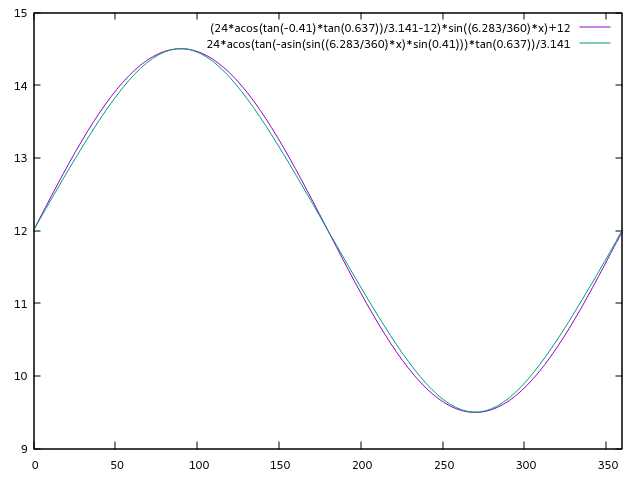
看看误差:
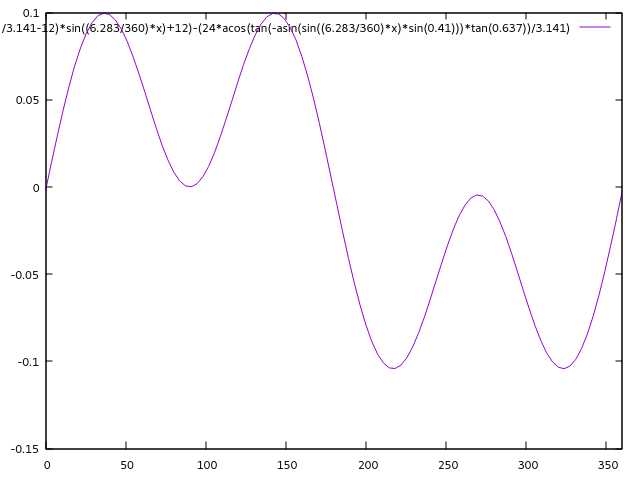
最大误差 \( \pm 6 \mathrm{min} \), 效果比较一般,表达式也没简化多少,看来还是得用原式。
有了白昼时间,日出日没时刻可用下面两式计算:
\( T_{sunrise} = T_{noon} - \frac{\mathrm{daytime}}{2} \) (1)
\( T_{sunset} = T_{noon} + \frac{\mathrm{daytime}}{2} \) (2)
问题又来了,正午 \( T_{noon} \) 不一定是 12:00:
首先,区时和地方时之间有可能会差不少,这会导致正午时刻偏离 12:00.
其次,由于太阳运动的不均匀(均時差),正午时刻也会偏离 12:00.
这两个效应会叠加。第一个问题好解决,只要知道时区中央经线的经度和当地的经度,就万事大吉了。第二个就不大好算了。《天文算法》中给出了一个近似公式(我把高阶项都扔掉了):
\( E‘ = T_{mean}-T_{true} = 4 \cdot [ \tan^2{(\frac{\varepsilon}{2})}\cdot \sin{2L}+2e\cdot \sin{(L-\bar{\omega})} ] \) ( E 的单位为分钟 )
其中 \(L\) 为太阳平黄经(即平太阳黄经,(假想的)平太阳以一个回归年为周期在黄道上做匀速圆周运动。可以近似地认为它等于上个春分和今天之间差的天数(或再乘以平太阳的角速度 \( \frac{{360}^{\circ}}{{365.2422}^{\mathrm{d}}} \) )),\(e\) 为地球轨道离心率,\( \bar{\omega} \) 为地球近日点(日心)黄经。\(e \approx 0.0167 \) 和 \( \bar{\omega}\approx {102.982}^{\circ} \) 在短时间内可看作常数。
作图(\(E\) 关于 \(L\) 的变化情况):
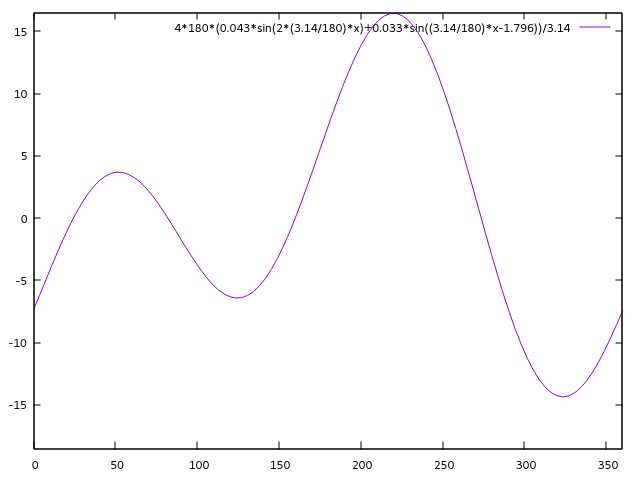
现在要求正午时间,令 \( T_{true} = 12:00 \), 解得:
\( T_{mean}=12:00+E‘ \)
补上区时和地方时的偏差,最终得到:
\( T_{noon}=12:00 + 4^{\mathrm{m}}\cdot(L_{zone}-L_{local}) + 4^{\mathrm{m}} \cdot [ \tan^2{(\frac{\varepsilon}{2})}\cdot \sin{2L}+2e\cdot \sin{(L-\bar{\omega})} ] \)
其中 \( L_{zone} \) 和 \( L_{local} \) 分别为时区中央经线的经度和当地的经度(东经为正)。
至此,大功告成,用 (1) 和 (2) 计算日出日没就可以了。
标签:
原文地址:http://www.cnblogs.com/li-hua/p/5593648.html