标签:
t检验和方差分析主要针对于连续变量,秩和检验主要针对有序分类变量,而卡方检验主要针对无序分类变量(也可以用于连续变量,但需要做离散化处理),用途同样非常广泛,基于卡方统计量也衍生出来很多统计方法。
卡方统计量是基于卡方分布的一种检验方法,根据频数值来构造统计量,是一种非参数检验方法。SPSS中在交叉表和非参数检验中,都可调用卡方检验。
卡方检验的主要有两类应用
一、拟合度检验
1.检验单个无序分类变量各分类的实际观察次数和理论次数是否一致
此类问题为单变量检验,首先要明确理论次数,这个理论次数是根据专业或经验已知的,原假设为观察次数与理论次数一致
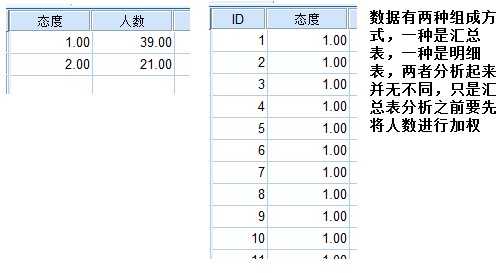
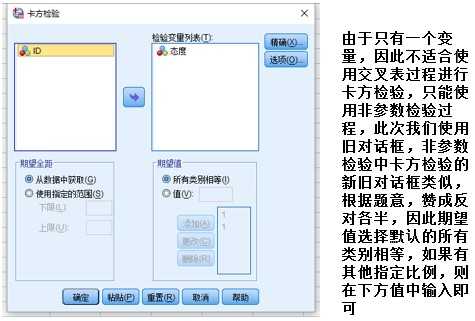
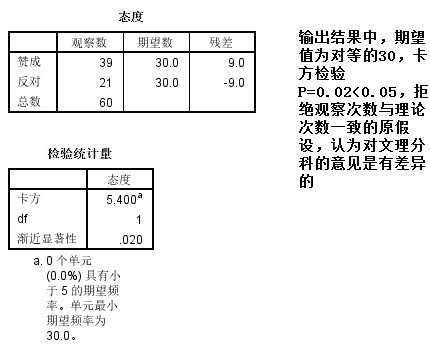
【例】:随机抽取60名高一学生,问他们文理要不要分科,回答赞成的39人,反对的21人, 问对分科的意见是否有显著的差异。
分析:如果意见没有差异,那么赞成反对的人数应该各半,即30次,因此理论次数为30
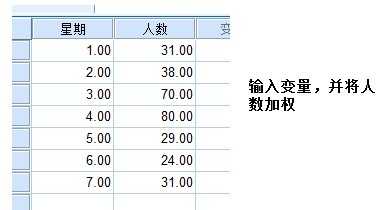
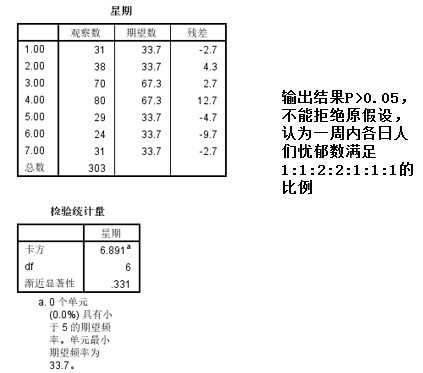
【例】:一周内各日患忧郁症的人数分布如下表所示,请检验一周内各日人们忧郁数是否满足1:1:2:2:1:1:1
本例中检验的理论次数就不是各半了,而是有一定的比例1:1:2:2:1:1:1
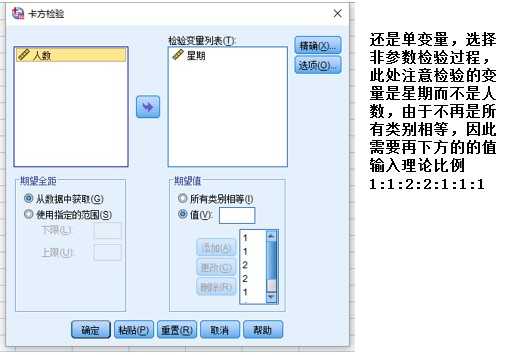
2.检验某分类变量各类别出现的概率是否相等 此类问题也属于单变量检验,例如掷硬币正反面出现的概率均为1/2,骰子每面出现的概率为1/6,原假设为变量各类别出现的概率相等
【例】:一个骰子投掷120次,记录掷得每个点数的次数,问该骰子是否存在问题 如果骰子是正常的,那么每个点数掷得的概率应该相等,操作方法和前面一样,也使用非参数检验过程,选择默认的所有类别相等
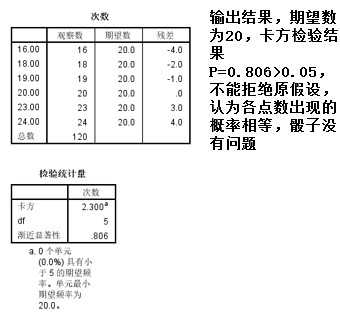
实际上,上面的第一个例子碰巧可以和本例互相转化,意见没有差异等同于赞成和反对出现的概率相等,而每个骰子点数出现的理论次数为120*1/6=20次
3.检验某连续变量分布是否和某种理论分布一致
卡方检验主要用于分类变量,但是也可以用于对连续变量的拟合度检验上,此类问题的基本思想是:将总体X的取值范围分成k个互不重叠的小区间A1...A2...Ak,把落入第i个小区间的样本值个数作为实际频数,所有实际频数之和等于样本容量,根据理论分布,可以算出总体X的值落入每个小区间Ai的概率Pi,于是nPi就是落入Ai的样本值的理论频数。有了实际频数和理论频数,就可以计算卡方统计量并进行卡方检验了。
二、独立性检验
独立性检验分析两变量之间是否相互独立,或者控制某种因素之后,两变量之间是否相互独立。原假设为两变量相互独立或两变量间的相互作用没有差别。
对于两变量一般采用列联表的形式记录观察数据,分为四格表和R*C列联表,根据卡方统计量和分类变量的类型,又衍生出一些相关系数,这在相关分析中已经讲过。
【例】:为了解男女在公共场所禁烟上的态度,随机调查100名男性和80名女性。男性中有 58人赞成禁烟,42人不赞成;而女性中则有61人赞成,19人不赞成。分析男女在公共场所禁烟的问题所持态度不同? 或者说禁烟态度是否随性别变化而变化
两变量之间的独立性,是指一个变量不随另一个变量的变化而变化,该问题的一种分析角度是分析男女在公共场所禁烟的问题所持态度不同,这看似和拟合性类似,但是其中涉及两个变量——性别和态度,因此属于独立性检验。
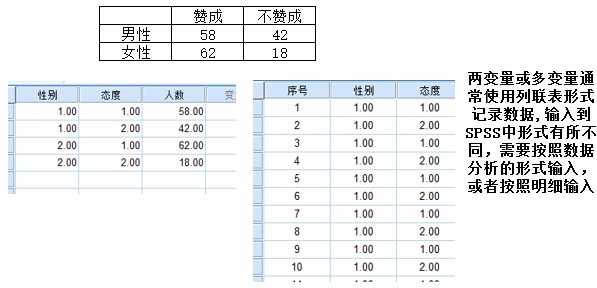
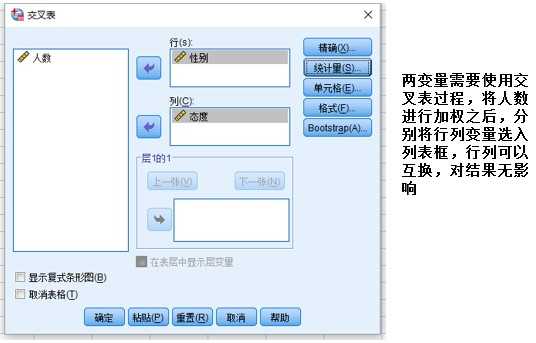

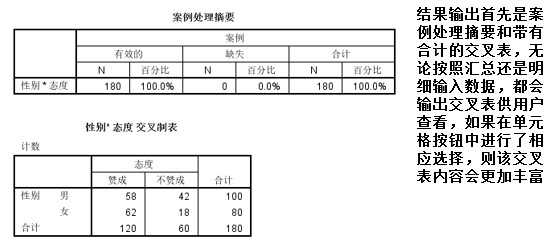
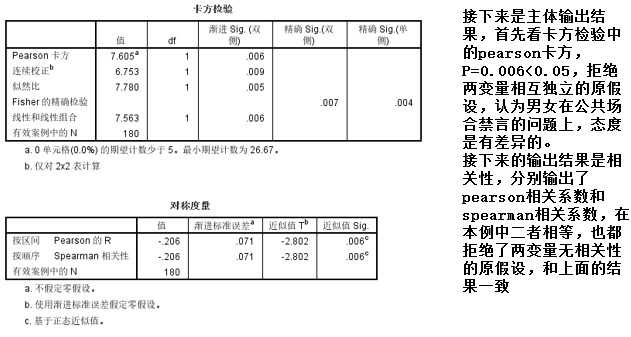
从表面上看,拟合性检验和独立性检验不论在列联表的形式上,还是在计算卡方的公式上都是相同的,所以经常被笼统地称为卡方检验。但是两者还是存在差异的。
首先,两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行,依照各类别分别计算其比例,属于拟合优度检验。如果抽样时并未事先分类,抽样后根据研究内容,把入选单位按两类变量进行分类,形成列联表,则是独立性检验。
其次,两种检验假设的内容有所差异。拟合优度检验的原假设通常是假设各类别总体比例等于某个期望概率,而独立性检验中原假设则假设两个变量之间独立。
最后,期望频数的计算不同。拟合优度检验是利用原假设中的期望概率,用观察频数乘以期望概率,直接得到期望频数。独立性检验中两个水平的联合概率是两个单独概率的乘积
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5595872.html