标签:
取p=29,求出椭圆曲线y^2=x^3+4x+20的全部解点
用穷举法求椭圆曲线
第一步:列表,求出0~28(0<=i<p)关于等式x^3+4x+20 mod29 的结果
可用程序完成此步骤:
代码如下:
#include<stdio.h>
int main()
{
int i,y,z;
printf("x x^3+4*x+20 \n");
for (i = 0; i < 29; i++)
{
y = i*i*i + 4 * i + 20;
z = y % 29;
printf( "%d %d\n", i, z);
}
}
计算结果如下图:
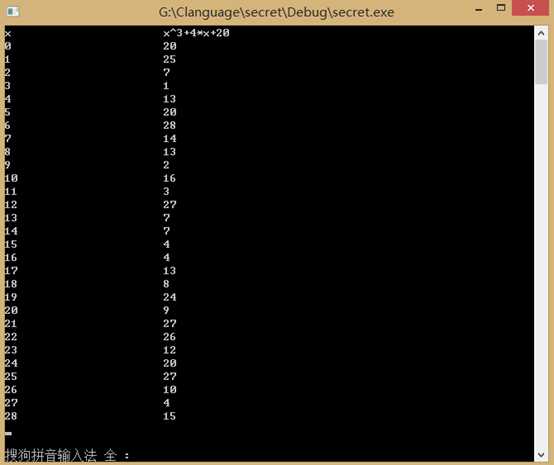
第二步,计算i(0<=i<p)的平方模29的结果
0~28的平方模29的结果为:
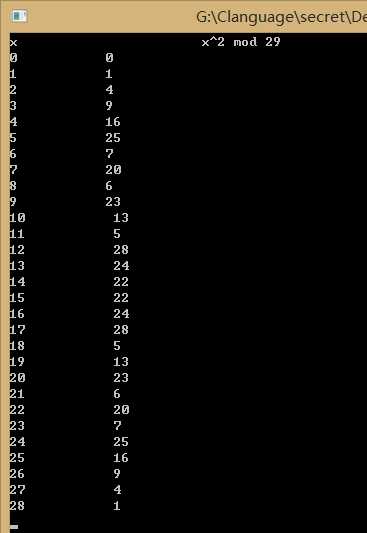
代码为:
#include<stdio.h>
int main()
{
int i, y;
printf("x x^2 mod 29\n");
for (i = 0; i < 29; i++)
{
y = i*i%29;
printf("%d %d \n",i,y);
}
}
第三步,通过对比i^3+4i+20 mod29的结果是否有i^2吗mod29与之相等,有的话在“是否模29的平方剩余”处写Y,并将对应的I写入y列
|
x |
X^3+4x+20 mod 29 |
是否模29的平方剩余 |
y |
|
0 |
20 |
Y |
7,22 |
|
1 |
25 |
Y |
5,24 |
|
2 |
7 |
Y |
6,23 |
|
3 |
1 |
Y |
1,28 |
|
4 |
13 |
Y |
10,19 |
|
5 |
20 |
Y |
7,22 |
|
6 |
28 |
Y |
12,17 |
|
7 |
14 |
N |
|
|
8 |
13 |
|
10,,19 |
|
9 |
2 |
N |
|
|
10 |
16 |
|
4,,25 |
|
11 |
3 |
N |
|
|
12 |
27 |
N |
|
|
13 |
7 |
|
6,23 |
|
14 |
7 |
|
6,,23 |
|
15 |
4 |
|
2,27 |
|
16 |
4 |
|
2,27 |
|
17 |
13 |
|
10,,19 |
|
18 |
8 |
N |
|
|
19 |
24 |
|
1316 |
|
20 |
9 |
|
3,26 |
|
21 |
27 |
N |
|
|
22 |
26 |
N |
|
|
23 |
12 |
N |
|
|
24 |
20 |
|
7,22 |
|
25 |
27 |
N |
|
|
26 |
10 |
N |
|
|
27 |
4 |
|
2,27 |
|
28 |
15 |
N |
|
|
说明 |
第一个程序结果 |
第一个和第二个程序对比结果 |
相应2个数加起来等于p。如第27行的7+22=29 |
然后将结果读出加上O点即可,即为
(0,7)(0,22)(1,5)(1,24)(2,6)(2,23)(3,1)(3,28)(4,10)(4,19)(5,7)(5,22)
(6,12)(6,17)(8,10)(8,19)(10,4)(10,25)(13,6)(13,23)(14,6)(14,23)(15,2)(15,27)
(16,2)(16,27)(17,10)(17,19)(19,13)(19,16)(20,3)(20,26)(24,7)(24,22)(27,2)(27,27)加上O点(∞,∞)
共37个解点
37位素数,所以,所以此群为循环群
标签:
原文地址:http://www.cnblogs.com/luanluan-/p/5596419.html