标签:
我很早就一直想写一篇文章,跟大家聊一聊: $$\frac{1}{1^2}+\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\frac{1}{5^2} +\cdots\ =\ \frac{π^2}{6}$$
但一直没有机会,这次放暑假正好有空,于是手就痒了,写下此文,供大家娱乐。
本文假设读者热爱数学,并且曾经掌握过高中数学知识。
首先我们要复习一下三角函数。
对于任意的角 $x$, 我们有 ${\sin^2 x}+\cos^2x=1$,这跟勾股定理是一回事。
接下来是一个重要的公式,需要读者自己画个图才能理解。
$$\sin(2x) = 2 \sin x \cos x$$
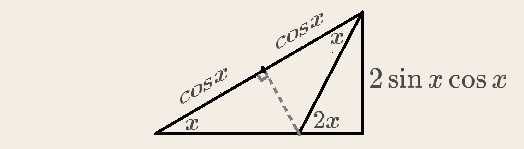
然后通过画出三角函数图像的方式,
我们还可以轻易验证
$$\cos x = \sin (x+\frac{π}{2})$$ 以及 $$\sin(π-x) = \sin x$$
现在我们可以开始证明了。
(该证明取自美国数学月刊2002年2月第109期 pp. 196-200 作者系Josef Hofbauer。)
由于 $\sin(2x) = 2 \sin x \cos x$,
所以 $$\sin x= 2 \sin(\frac{x}{2})\cos(\frac{x}{2})$$取倒数,平方,得 $$\frac{1}{\sin^2 x} = \frac{1}{4}\frac{1}{\sin^2(x/2)\cos^2(x/2)}$$然后根据 ${\sin^2 x}+\cos^2x=1$
我们有
$$\frac{1}{\sin^2 x} = \frac{1}{4}\frac{\sin^2 (x/2)+\cos^2 (x/2)}{\sin^2(x/2)\cos^2(x/2)}=\frac{1}{4}( \frac{1}{\cos^2(x/2)} + \frac{1}{\sin^2(x/2)})$$接下来利用性质,$\cos(x/2) = \sin((x+π)/2)$
就得到核心关系式:
$$\ \ \ \ \ \ \frac{1}{\sin^2 x} = \frac{1}{4} (\frac{1}{\sin^2\frac{x}{2}} + \frac{1}{\sin^2\frac{x+π}{2}}) \ \ \ \ \ \ \ \ \ \ (*) $$
这是证明中最最核心的一步,我们称这个关系式为“(*)”。
现在我们根据定义可知 $$\sin(π/2) =\, \sin90°=1$$
然后平方,取倒数,并反复利用(*)式,我们有
\begin{align}
1 & = \frac{1}{\sin^2(π/2)} \\
& =\frac{1}{4} (\frac{1}{\sin^2(π/4)} + \frac{1}{\sin^2(3π/4)}) \\
& =\frac{1}{4^2} (\frac{1}{\sin^2(π/8)} + \frac{1}{\sin^2(3π/8)}+\frac{1}{\sin^2(5π/8)} + \frac{1}{\sin^2(7π/8)})\\
& = \dots
\end{align}
可以这样一直做下去。
现在,利用恒等式 $\sin(π-x)=\sin x$
就能得到
\begin{align}
1 & =\frac{2}{4^2} (\frac{1}{\sin^2(π/8)} + \frac{1}{\sin^2(3π/8)}) \\
& =\frac{2}{4^3} (\frac{1}{\sin^2(π/16)} + \frac{1}{\sin^2(3π/16)}+\frac{1}{\sin^2(5π/16)} + \frac{1}{\sin^2(7π/16)}) \\
& ={\frac{2}{4^4} (\frac{1}{\sin^2(π/32)} + \frac{1}{\sin^2(3π/32)}+\frac{1}{\sin^2(5π/32)} +\dots + \frac{1}{\sin^2(15π/32)})}\\
& = \dots
\end{align}
我们将这个关系称为“(**)”式。
有读者可能要问,为什么要这样做,其实原因马上就很清楚了,目的只有一个,让所有 $\sin()$里的值都是锐角。
因为对于锐角$x$,我们有 $\sin x < x < \tan x$ 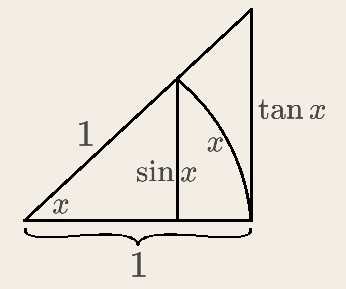
取倒数,平方,得
$$\frac{1}{\sin^2 x} > \frac{1}{x^2} > \frac{1}{\tan^2 x}$$而我们又知道
$$\frac{1}{\tan^2 x}=\frac{\cos^2 x}{\sin^2 x}=\frac{1-\sin^2 x}{\sin^2 x}=\frac{1}{\sin^2 x}-1$$所以
$$\frac{1}{\sin^2 x}-1<\frac{1}{x^2}<\frac{1}{\sin^2 x}$$
现在结合前面推导的关系(**):
$$
1 ={\frac{2}{4^4} (\frac{1}{\sin^2(π/32)} + \frac{1}{\sin^2(3π/32)}+\frac{1}{\sin^2(5π/32)} +\dots + \frac{1}{\sin^2(15π/32)})}
$$
我们可以得到如下不等关系
\begin{align}
1-\frac{2}{4^4}*2^3 & <{\frac{2}{4^4} (\frac{1}{(π/32)^2} + \frac{1}{(3π/32)^2}+\frac{1}{(5π/32)^2} +\dots + \frac{1}{(15π/32)^2})} < 1\\
1-\frac{2}{4^4}*2^3 & < {\frac{2}{4^4}* 4^5 (\frac{1}{π^2} + \frac{1}{(3π)^2}+\frac{1}{(5π)^2} +\dots + \frac{1}{(15π)^2})} <1\\
1-\frac{1}{2^4}& < {\ 8\,(\frac{1}{π^2} + \frac{1}{(3π)^2}+\frac{1}{(5π)^2} +\dots + \frac{1}{(15π)^2})} <1
\end{align}
(各位读者请注意,刚才这三个不等关系可能需要花时间仔细读懂。尤其是(9),是全文中最难理解的一步,希望读者能耐心地读懂:如何可以从之前两个公式,得到该不等关系。)
通过观察,我们可以发现,之前在(**)中,我们只用到$$1 = {\frac{2}{4^4} (\frac{1}{\sin^2(π/32)} + \frac{1}{\sin^2(3π/32)}+\frac{1}{\sin^2(5π/32)} +\dots + \frac{1}{\sin^2(15π/32)})}$$
如果在之前,多利用(*)几次,
使得(**)中 $\sin$ 的项数由 $8=2^3$ 项 增长为 $2^n$ 项
则有
$$1-\frac{1}{2^{n+1}} < {8(\frac{1}{π^2} + \frac{1}{(3π)^2}+\frac{1}{(5π)^2} +\cdots +
\frac{1}{((2^{n+1}-1)π)^2})}<1$$
当n很大时,$\frac{1}{2^{n+1}}$ 可以忽略不计,所以我们有
$${\,8\,(\frac{1}{π^2} + \frac{1}{(3π)^2}+\frac{1}{(5π)^2}+\frac{1}{(7π)^2} +\cdots)}= 1$$
即 $$\frac{1}{1^2}+\frac{1}{3^2} +\frac{1}{5^2} +\frac{1}{7^2} +\cdots =\frac{π^2}{8} $$
现在我们离结论只有一步之遥,
令 $$\zeta(2) = \frac{1}{1^2}+\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\frac{1}{5^2} +\cdots\ $$ 那么 $$ \frac{\zeta(2)}{4} = \frac{1}{2^2}+\frac{1}{4^2} +\frac{1}{6^2} +\frac{1}{8^2} +\frac{1}{10^2} +\cdots $$ 两式相减,就能得到 $$\zeta(2)-\frac{\zeta(2)}{4} = \frac{1}{1^2}+\frac{1}{3^2} +\frac{1}{5^2} +\frac{1}{7^2} +\cdots =\frac{\pi^2}{8}$$所以 $3\zeta(2) /4 = π^2/8$,求得 $\zeta(2) = π^2/6$,即我们要证的结论:
$$\frac{1}{1^2}+\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\frac{1}{5^2} +\cdots\ =\ \frac{π^2}{6}$$
怎么样,好玩吧,数学永远是这样,用最巧妙的逻辑链条构造最美丽的证明。
只要有一点点好奇心,和足够的耐心,人人都可以享受数学的乐趣。
祝大家暑假愉快。
贾博名
2014年6月20日 于 美国俄亥俄州哥伦布市
(最新一次更新于2016年6月18日,再次感谢孙豪同学对本文初稿的认真阅读,并指出了多处笔误。)
标签:
原文地址:http://www.cnblogs.com/jiab/p/5597738.html