标签：
机器学习
这是记录自学的过程，目前的理论基础就是：大学高等数学+线性代数+概率论。编程基础：C/C++,python在观看机器学习实战这本书，慢慢介入。相信有读过以上三门课的人完全可以开始自学机器学习了，当然我上面这三门课学的一般，所以你只知道有这么一个公式或名词，不懂可以百度之深究之。在写这篇文章的时候作者机器学习还没学完，故文章中的错误还请不吝指出。再次声明，系列文章只是分享学习过程，学习点滴，不能保证文章的技术含量。后续再技术的不断完善中，我会重新再捋一遍这个学习过程，纠正其中错误。
目前的学习方法如下：
理论：斯坦福Andrew NG machine learning，系列课程。
代码实战：引用书籍 机器学习实战（python）。
演变：基于C/C++ 在linux下实现部分机器学习过程。
真枪实战： 研究一个案例，建模选择合适的机器学习算法，分析数据。
一、Logistic Regression和Sigmoid函数
关于Logistic Regression的定义，网上颇多，这里不再赘述。按道理来说机器学习的步骤是分析一个案例，然后选择一个函数模型h(x),引用一段andrew的原话：
We could approach the classification problem ignoring the fact that y is
discrete-valued, and use our old linear regression algorithm to try to predict
y given x. However, it is easy to construct examples where this method
performs very poorly. Intuitively, it also doesn’t make sense for hθ(x) to take
values larger than 1 or smaller than 0 when we know that y ∈ {0, 1}.
linear regression的例子，其实我们高中就有接触过，所谓的一次函数类似y=ax+b，就是线性回归的函数简单单参数模型，这里建模的目的是为了pridict y，显然y的值不可确定范围。但是顾名思义Logistic
Regression，它的预测结果范围是可知的，比如Y的值就有明确定义 y ∈ {0, 1}.那么就要重新寻找函数模型h(x).
有些技术总是站在巨人的肩膀上，大学课程中显然已经有接触到符合上述定义的函数模型：
至于有些人会问，初学者怎么会知道选择这样一个模型，那我只能说可能你对高等数学的内容有点忘了，选择这样一个函数模型原因在于，g(z)的取值范围在0~1之间，可以规定<0.5属于0，>0.5属于1.所以选择什么函数模型，是基于实际问题的分析，然后在数学模型中筛选出一种合适的函数。此函数学名 Sigmoid：是一种阶跃函数，当横坐标轴刻度足够大时，它的图像看上去就像一个阶跃函数：
二、最佳回归系数的理论推导
如上我们选择Sigmoid函数。g(z)中的z可以理解为数据输入，数据可能不止一类，我们可以定义一下公式：
z = w0x0+w1x1+w2x2+w3x3+.......+wnxn.
上述，x0,x1,x2......为输入的数据，w0,w1,w2......为对应的参数，也就是我们要通过训练大量数据得出的回归系数。为了便于理解线面选择一个有两个数据输入类型(X1,X2)的例子进一步分析。这里一般都假设x0=1.
好了现在是确定了分类器的函数，接下的目的是如何预测Y呢？引入一个数据分析便于理解：
上述数据集摘自机器学习实战中的数据片段，可以忽略他的实际意义，前面两列为输入数据X1，X2,后面一列为分类情况，可以看出有两个类别，基于这样的数据类型，我们就可以用上述Sigmoid函数模型来预测输入其他数据后的分类结果。
接下来要做的事就是如何得出最佳回归系数，先了解一下理论知识。我们最终确定回归系数也是通过让h(x)不断接近y(数据集中实际的值)。那么我们刚开始回归系数有个初始值，那么得出来的h(x)的值肯定偏差较大，这里引入一个cost function的概念：J(w) = h(x) - y. 我们训练数据的目的就是让J(w)达到最小值，到这里你可能注意到h(x)的模型中含有e，单纯的加减法只会让操作更加复杂，另外更为权威的解释就是此时J(w)是一个非凸函数，这意味着J(w)有许多局部最值，这样我们很难找到他的最值（通过梯度上升）。针对这种情况，数学中有另外一种方法来最小化它。
我们先对g(z)求导：
g(z)的导函数看起来有点门道，当g(z)取0或者1时，g(z)有极值?也就是当z -> 正无穷：g(z) 接近1；z -> 负无穷：g(z) 接近0。(g(z)
= h.(x))
不妨假设：
假设我们数据集都是互相独立的，那么就可以用极大值似然估计法来求出上面的最大值,其作用为：在已知试验结果（即是样本）的情况下，用来估计满足这些样本分布的参数，把可能性最大的那个参数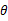
作为真实
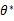的参数估计。
我们都只求似然函数的极大值方法就是求导，上述中的θ就是我们要确定的回归系数，似然函数的极大值受θ
影响，所以在寻找极大值的过程中我们采用了一个算法：梯度上升。关于梯度的概念：寻找某个函数的最大值，最好的方法是沿着这个函数的梯度的方向探寻。梯度的简单理解就是对某个点的求导。
我们定义以下式子来更新我们回归系数：
θ
:=
θ +
α?θ?(θ)
α学习速率，可以理解为步长，更新回归系数的速度，由我们自己初始化定义。
对似然函数的求导得到梯度:
代入上式：
三、梯度上升算法的代码实现
以上的推导最终得到上面的一个式子，梯度上升算法的核心。可以看到影响回归系数的主要还是数据本身和预测值与实际值之间的误差。下面是梯度上升的伪代码:
每个回归系数初始化为1；
重复R次：
计算整个数据集的梯度；
使用alpha * gradient 来更新回归系数的值（有可能是向量）；
返回回归系数。
以下讲解机器学习实战中提供的源代码：
1.load数据from file。
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#这里人为的引入一个数据1，即x0.
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
2.sigmoid 函数
def sigmoid(inX):
return 1.0/(1+exp(-inX))
3.梯度上升算法:
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #转化成矩阵
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix) #获取矩阵属性，m行n列
alpha = 0.001 #init alpha
maxCycles = 500 #define the recycle times
weights = ones((n,1)) #initialize the 回归系数，为n行一列单位向量
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #用初始值回归系数乘以数据，可以看到
#这边是整个数据集乘以回归系数，矩阵相乘： m*n 乘以 n*1，得到m行一列的单位向量,
#也就是得到预测值h(x).
error = (labelMat - h) #误差值，相当于(y - h(x))。
weights = weights + alpha * dataMatrix.transpose()* error #更新回归系数，代码中
#对应上述式子：θj := θj + α (y(i) ? hθ(x(i))) * xj( i).其中error为(y(i) ? hθ(x(i)))
#dataMatrix为输入数据集x,transpose()为转置，<span style="font-family: Arial, Helvetica, sans-serif;">dataMatrix转置之后为n*m 与 m*1的error可以相乘。</span>
return weights
上述代码保存到logRegres.py中，在python实践验证:
>>>import logRegres
>>>dataArr,labelMat = logRegres.loadDataSet()
>>>logRegres.gradAscent(dataArr,labelMat )
将会得到回归系数向量。
matrix：
([[ 4.12414349],
[ 0.48007329],
[-0.6168482 ]])
下面代码是将整个训练情况和数据分布用图像画出来：
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
可以得到如图：
机器学习系列-Logistic Regression(1)
标签：
原文地址：http://blog.csdn.net/w401229755/article/details/51712581
VM1.png)
作为真实
的参数估计。