Correlation Filter in Visual Tracking系列一：Visual Object Tracking using Adaptive Correlation Filters 论文笔记

 

　　Visual Object Tracking using Adaptive Correlation Filters 一文发表于2010的CVPR上，是笔者所知的第一篇将correlation filter引入tracking领域内的文章，文中所提的Minimum Output Sum of Squared Error(MOSSE)，可以说是后来CSK、STC、Color Attributes等tracker的鼻祖。Correlation Filter（以下简称CF）源于信号处理领域，后被运用于图像分类等方面。Correlation包含Cross-correlation和Auto-correlation，在这里我们一般指的就是Cross-correlation。首先看看维基百科上Cross-correlation的定义，假设有ff和gg两个函数（信号），其cross-correlationf?gf?g定义为

 

(f?g)(τ)=def∫∞−∞f∗(t)g(t+τ)dt(1)(f?g)(n)=def∑−∞∞f∗[m]g(m+n)(f?g)(τ)=def?∫−∞∞f∗(t)g(t+τ)dt(1)(f?g)(n)=def?∑−∞∞f∗[m]g(m+n)

 

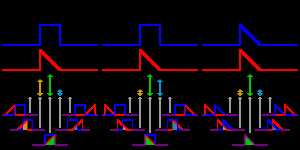
　　其中f∗f∗表示ff的复共轭，correlation的直观解释就是衡量两个函数在某个时刻ττ的相似程度，如下图所示。考虑一个最简单的例子，假设ff和gg的形状一样，但是相差了若干个时刻，那么f★gf★g取得最大值的时候一定是ff和gg对齐的时候（没谁比自己和自己更像了吧…），但因为两者有时间差，所以要取得最大值，就要把其中一个在时间轴上进行平移，所以g(t+τ)g(t+τ)就代表把gg平移ττ个时刻。其实Convolution和Cross-correlation在图像处理的书里一般都会提到，这里就不多叙述了。

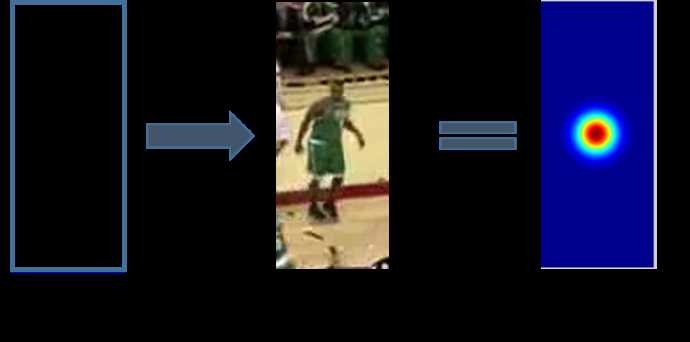
　　而Correlation Filter应用于tracking方面最朴素的想法就是：相关是衡量两个信号相似值的度量，如果两个信号越相似，那么其相关值就越高，而在tracking的应用里，就是需要设计一个滤波模板，使得当它作用在跟踪目标上时，得到的响应最大，如下图所示:

 

　　CF方法最大的优势在于其速度之快，是任何其他跟踪方法都无法比拟的，如本篇所写的MOSSE，其速度可以到669帧每秒，把跟踪算法从real time 级别提升到了high speed级别；而且其跟踪准确率高，在wuyi他们的online benchmark上，带核函数的CSK方法可以得到73%左右的准确率。有着如此明显的优点，相信此类方法将会成为跟踪领域内继sparse方法的又一重要分支。

　　 好，言归正传，我们先来介绍CF中的元老，MOSSE。按照我们刚刚的思路，我们需要寻找一个滤波模板，使得它在目标上的响应最大，那么写成公式就是如(2)所示

　　　　　　　　g=h ★f(2)g=h ★f(2)                                                            

　　其中gg表示响应输出，ff表示输入图像，hh表示我们的滤波模板。 gg可以为任意形状的响应输出，在上图的示意图里我们就假设它为gaussian形状。那么显然，我们只要求出hh就可以了。这样做看起来很简单，但为何CF类方法的速度如此之快呢？就是因为在求解等一系列操作中，都利用了快速傅里叶变换FFT。由卷积定理的correlation版本可知，函数互相关的傅里叶变换等于函数傅里叶变换的乘积，即如(2)式所示：

　　　　　　　　Fh ★f=(Fh)∗⊙Ff(3)Fh ★f=(Fh)∗⊙Ff(3)                                      

　　其中FF表示傅里叶变换，⊙⊙表示点乘。那么假设ff所含的像素个数为nn，而已知FFT的时间开销为O(nlogn)O(nlog?n)，因此式(3)的计算开销也为O(nlogn)O(nlog?n)！远比其他跟踪算法要快！明白这一点后，本篇论文的精华你已经掌握了。剩下的就是如何计算hh了，为了表达的方便起见，我们设Ff=FFf=F，(Fh)∗=H∗(Fh)∗=H∗，Fg=GFg=G，那么我们就有

　　　　　　　　H∗=GF(4)H∗=GF(4)                                                              

　　但是在实际应用中，因为目标的外观变换等因素影响，我们需要同时考虑目标的mm个图像作为参考，以提高模型的鲁棒性，那么就有如(5)的目标函数了：

　　　　　　　　minH∗∑i=1m|H∗Fi−Gi|2(5)minH∗∑i=1m|H∗Fi−Gi|2(5)

　　求解式(5)并不困难，而且根据卷积定理，在频率域的操作都是元素级别的，因此我们可以分别求解H∗H∗中的每一个元素H∗w,vHw,v∗，那么(5)就可以变为：

 　　　　　　　　minH∗w,v∑i=1m|H∗w,vFw,v,i−Gw,v,i|2(6)minHw,v∗∑i=1m|Hw,v∗Fw,v,i−Gw,v,i|2(6)  

 　　然后对(6)式求导并使其为0即可求解，但要注意的是，论文中特别指出在复数域的求导与在实数域的有一点区别：

 

∂∂H∗w,v∑i=1m(H∗w,vFw,v,i−Gw,v,i)⋅(H∗w,v　　Fw,v,i−Gw,v,i)∗=0⇒∂∂H∗w,v∑i=1mH∗w,vFw,v,i⋅Hw,vF∗w,v,i−H∗w,vFw,v,iG∗w,v,i−Hw,vF∗w,v,iGw,v,i+Gw,v,iG∗w,v,i=0⇒∑i=1mFw,v,i⋅Hw,vF∗w,v,i−Fw,v,iG∗w,v,i=0⇒Hw,v=∑i=1mFw,v,iG∗w,v,i∑i=1mFw,v,iF∗w,v,i(7)∂∂Hw,v∗∑i=1m(Hw,v∗Fw,v,i−Gw,v,i)⋅(Hw,v∗　　Fw,v,i−Gw,v,i)∗=0⇒∂∂Hw,v∗∑i=1mHw,v∗Fw,v,i⋅Hw,vFw,v,i∗−Hw,v∗Fw,v,iGw,v,i∗−Hw,vFw,v,i∗Gw,v,i+Gw,v,iGw,v,i∗=0⇒∑i=1mFw,v,i⋅Hw,vFw,v,i∗−Fw,v,iGw,v,i∗=0⇒Hw,v=∑i=1mFw,v,iGw,v,i∗∑i=1mFw,v,iFw,v,i∗(7)

 

　　按以上方式处理所有HH中的所有元素，得到：

　　　　　　　　H=∑i=1mFi⊙G*i∑i=1mFi⊙F*i(8)H=∑i=1mFi⊙Gi*∑i=1mFi⊙Fi*(8)                                                                                          

　　就可以开始跟踪了。在跟踪的过程中，我们只需要把以上模板与当前帧的图像作相关操作，将得到的响应结果中最大的那点对应坐标作为目标在当前帧位置就可以了（相当于在2维上平移我们的模板）。然后，模板的更新方式可以按照如下的方式进行：

　　　　　　　　Ht=(1−η)Ht−1+ηH(t)(9)Ht=(1−η)Ht−1+ηH(t)(9)                                            

　　H(t)H(t)表示在第tt帧求得的滤波模板，ηη为一经验常数。

　　本文的内容大体就这样了，剩下的就是在(8)上面进行一些修改，比如在分母里引进一个εε作为正则化的参数，或者分别求HiHi然后作平均等，都是一些小的技巧。总得来说，MOSSE方法开创了CF在tracking方面的先河，而在后面的一系列文章里，我们将介绍一系列用概率论、岭回归等理论对其作进一步提升的文章。