标签:
http://blog.csdn.net/pipisorry/article/details/51695283
这篇文章主要讲:熵, 联合熵(joint entropy),条件熵(conditional entropy),相对熵(relative entropy,KL 距离),交叉熵(cross entropy),困惑度(perplexity),互信息(mutual information)。
在信息论中,熵是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。这里, 消息代表来自分布或数据流中的事件、样本或特征。(熵最好理解为不确定性的量度而不是确定性的量度,因为越随机的信源的熵越大。)
来自信源的另一个特征是样本的概率分布。这里的想法是,比较不可能发生的事情,当它发生了,会提供更多的信息。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。由于一些其他的原因(下面会有解释),把信息(熵)定义为概率分布的对数的相反数是有道理的。
事件的概率分布和每个事件的信息量构成了一个随机变量,这个随机变量的均值(即期望)就是这个分布产生的信息量的平均值(即熵)。采用概率分布的对数作为信息的量度的原因是其可加性。例如,投掷一次硬币提供了1 Sh的信息,而掷 m 次就为 m 位。更一般地,你需要用 log2(n) 位来表示一个可以取 n 个值的变量。
在1948年,克劳德·艾尔伍德·香农将热力学的熵,引入到信息论,因此它又被称为香农熵。
假设一篇文章的标题叫做“黑洞到底吃什么”,包含词语分别是 {黑洞, 到底, 吃什么}, 我们现在要根据一个词语推测这篇文章的类别。哪个词语给予我们的信息最多?很容易就知道是“黑洞”,因为“黑洞”这个词语在所有的文档中出现的概率太低啦,一旦出现,就表明这篇文章很可能是在讲科普知识。而其他两个词语“到底”和“吃什么”出现的概率很高,给予我们的信息反而越少。
如何用一个函数 h(x) 表示词语给予的信息量呢?第一,肯定是与 p(x) 相关,并且是负相关。第二,假设 x 和 y 是独立的(黑洞和宇宙不相互独立,谈到黑洞必然会说宇宙),即 p(x,y) = p(x)p(y), 那么获得的信息也是叠加的,即 h(x, y) = h(x) + h(y)。满足这两个条件的函数肯定是负对数形式:
对假设一个发送者要将随机变量 X 产生的一长串随机值传送给接收者, 接受者获得的平均信息量就是求它的数学期望:
这就是熵的概念。另外一个重要特点是,熵的大小与字符平均最短编码长度是一样的(shannon)。设有一个未知的分布 p(x), 而 q(x) 是我们所获得的一个对 p(x) 的近似,按照 q(x) 对该随机变量的各个值进行编码,平均长度比按照真实分布的 p(x) 进行编码要额外长一些,多出来的长度这就是 KL 散度(之所以不说距离,是因为不满足对称性和三角形法则),即:
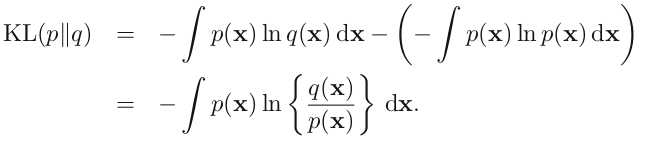
如果有一枚理想的硬币,其出现正面和反面的机会相等,则抛硬币事件的熵等于其能够达到的最大值。我们无法知道下一个硬币抛掷的结果是什么,因此每一次抛硬币都是不可预测的。
因此,使用一枚正常硬币进行若干次抛掷,这个事件的熵是一比特,因为结果不外乎两个——正面或者反面,可以表示为0, 1编码,而且两个结果彼此之间相互独立。若进行n次独立实验,则熵为n,因为可以用长度为n的比特流表示。
但是如果一枚硬币的两面完全相同,那个这个系列抛硬币事件的熵等于零,因为结果能被准确预测。现实世界里,我们收集到的数据的熵介于上面两种情况之间。
另一个稍微复杂的例子是假设一个随机变量X,取三种可能值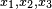 ,概率分别为
,概率分别为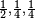 ,那么编码平均比特长度是:
,那么编码平均比特长度是: 。其熵为3/2。
。其熵为3/2。
因此熵实际是对随机变量的比特量和顺次发生概率相乘再总和的数学期望。
熵又称为自信息(self-information),表示信源 X 每发一个符号(不论发什么符号)所提供的平均信息量。熵也可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大,它的不确定性越大。那么,正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量用以确定其值。
依据Boltzmann‘s H-theorem,香农把随机变量 X 的熵值 Η(希腊字母Eta)定义如下,其值域为 {x1, ...,xn}:
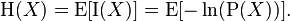
其中, P 为 X 的概率质量函数(probability mass function),E 为期望函数,而 I(X) 是X 的信息量(又称为自信息)。I(X) 本身是个随机变数。
当取自有限的样本时,熵的公式可以表示为:

Note: 熵的单位通常为比特,但也用Sh、nat、Hart计量,取决于定义用到对数的底。在这里 b 是对数所使用的底,通常是 2, 自然常数 e,或是10。当b = 2,熵的单位是bit;当b = e,熵的单位是nat;而当b = 10,熵的单位是 Hart。
pi = 0时,对于一些i值,对应的被加数0 logb 0的值将会是0,这与极限一致。

联合熵实际上就是描述一对随机变量平均所需要的信息量。
定义事件 X 与 Y 分别取 xi 和 yj 时的条件熵为

其中 p(xi, yj) 为 X = xi 且 Y = yj 时的概率。这个量应当理解为你知道Y 的值前提下随机变量 X 的随机性的量。
相对熵常被用以衡量两个随机分布的差距。当两个随机分布相同时,其相对熵为0。当两个随机分布的差别增加时,其相对熵也增加。
如果一个随机变量 X ~ p(x),q(x)为用于近似 p(x)的概率分布,那么,随机变量 X 和模型 q 之间的交叉熵定义为:
交叉熵的概念用以衡量估计模型与真实概率分布之间的差异。
在设计语言模型时,我们通常用困惑度来代替交叉熵衡量语言模型的好坏。给定语言L的样本
语言模型设计的任务就是寻找困惑度最小的模型,使其最接近真实的语言。
如果 (X, Y) ~ p(x, y),X, Y 之间的互信息 I(X; Y)定义为:
I (X; Y) = H(X) – H(X | Y) (11)
根据H(X) 和 H(X|Y) 的定义:
互信息 I (X; Y) 是在知道了 Y 的值以后 X 的不确定性的减少量,即Y的值透露了多少关于X 的信息量。
Note: 互信息 I (X; Y)可为正、负或0。
由于 H(X|X) = 0, 所以, H(X) = H(X) – H(X|X) = I(X; X)
这一方面说明了为什么熵又称自信息,另一方面说明了两个完全相互依赖的变量之间的互信息并不是一个常量,而是取决于它们的熵。
物理学家和化学家对一个系统自发地从初始状态向前演进过程中,遵循热力学第二定律而发生的熵的变化更感兴趣。在传统热力学中,熵被定义为对系统的宏观测定,并没有涉及概率分布,而概率分布是信息熵的核心定义。
注意,这里的边缘概率是基于每个音节的,其值是基于每个字符的概率的两倍,因此,每个字符的概率值应该为相应边缘概率的1/2,即:
p: 1/16 t: 3/8 k: 1/16 a: 1/4 i: 1/8 u: 1/8
求联合熵可以有几种方法,以下我们采用连锁规则方法可以得到:
from: http://blog.csdn.net/pipisorry/article/details/51695283
ref: [http://zh.wikipedia.org]
标签:
原文地址:http://blog.csdn.net/pipisorry/article/details/51695283