标签:
并查集(UnionSet)是一种树型的数据结构,用于处理一些不相交集合)的合并及查询问题。常常在使用中以森林来表示。
并查集实现了将N个不同的元素分成一组不相交的集合。开始时,每个元素就是一个集合,然后按规律将两个集合进行合并。
比如:现在有 0,1,2,3,4,5,6,7,8,9 总共10个元素。它们组成了3个集合,如图:
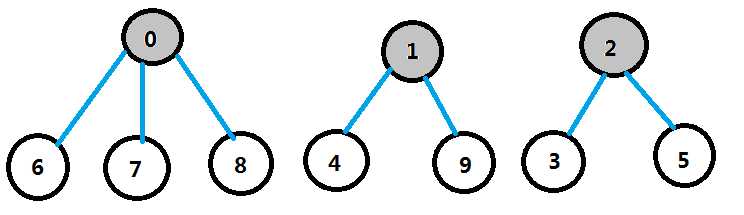
开始时,将每个元素都当做一个单元素的集合,并将每个元素都初始化为-1,如图:

根据集合按规律将两两集合进行合并, 6、7、8属于0这个集合,所以把6、7、8这三个位置都置0,而0这个位置减去3;1和2这两个集合类似,4和9都属于1这个集合,所以将4、9这两个位置都置为1,并将位置1的数据减2;3、5同属于集合2,所以将位置3、5的数据置为2,将位置2的数据减去2,即:

这样我们可以根据负数的个数清晰的看出有几个集合,并且我们也可以清晰的看出某节点是属于哪个集合的。有3个负数,所以有3个集合,3、5位置数据为2,所以它们属于集合2;6、7、8位置的数据都为0,所以它们都属于集合0;4、9属于集合集合1.
集合的合并:
形如:
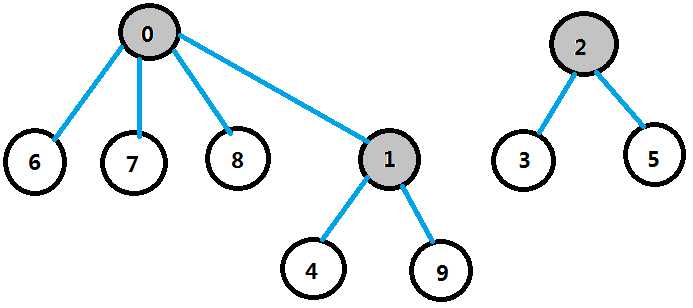
把集合1合并到集合0中,集合1有1、4、9三个元素,所以,将位置1设置为0,并将位置0的数据减去3,即:
由上图我们可以看出4、9属于集合1,集合1又属于集合0;此时数组中共有2个负数,因此有两个集合!
代码实现:
class UnionSet
{
public:
UnionSet(size_t size)
:_size(size)
, _array(new int[size])
{
for (int i = 0; i < size; i++)
{ //将集合的每个元素都初始化为-1
_array[i] = -1;
}
}
//合并两个集合
void Merge(int root1, int root2)
{
//找到root1所在集合的代表元素和root2所在集合的代表元素,链接
while (_array[root2] >= 0)
{
root2 = _array[root2];
}
while (_array[root1] >= 0)
{
root1 = _array[root1];
}
_array[root1] += _array[root2];
_array[root2] = root1;
}
//查找root对应集合的(根)代表元素
int Find(int root)
{
while (_array[root]>=0)
{
root = _array[root];
}
return root;
}
//打印
void Print()
{
for (int i = 0; i < _size; i++)
{
cout << _array[i] << " ";
}
cout << endl;
}
public:
int* _array;
size_t _size;
};
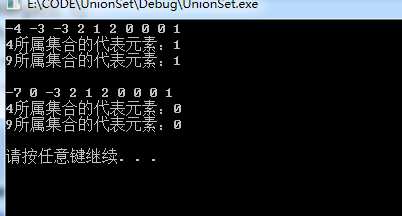
笔试题:
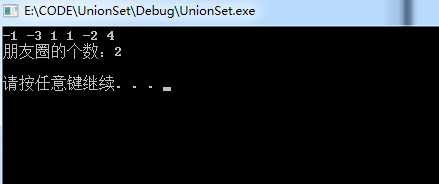
假如已知有n个人和m对好友关系(存于数组r),如果两个人是直接的或间接的好友关系(好友的好友的好友....),则认为他们属于同一好友圈,请求出这n个人中有几个好友圈。
例如:n=5,m=3,r={{1,2},{2,3},{4,5}},表示有5个人,1和2是好友,2和3是好友,4和5是好友,则1.2.3属于一个朋友圈,4.5属于一个另朋友圈,结果为两个朋友圈。
最后请分析所写代码的时间、空间复杂度。
这个题用利用并查集实现会比较简易和高效!
需要建立一个函数来计算朋友圈的个数:
//计算朋友圈个数
int friends(int n, int m, int r[][2]) //n元素个数,m为每个朋友圈元素个数
{
UnionSet uf(n + 1);
//初始化朋友圈
for (int i =0 ; i <= m; i++)
{
int first = r[i][0];
int second = r[i][1];
uf.Merge(first, second);
}
uf.Print();
//计算朋友圈的个数
int count = 0;
for (int i = 1; i <= n; i++)
{
if (uf._array[i] < 0)
{
count++;
}
}
return count;
}
标签:
原文地址:http://www.cnblogs.com/Lynn-Zhang/p/5610172.html