标签:
近来,了解了一下SVM(支持向量机 support vector machine)的原理。顺便把自己理解的内容整理一下。
不讲背景啦,直接切入主题。
一、 什么是支持向量机
好比说,我们现在在一个平面上有许多的圈圈和叉叉,如图1.1所示。
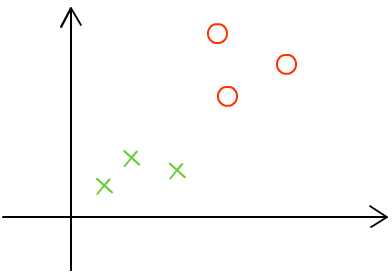
图1.1
现在需要一条直线将圈圈和叉叉分开,可以想象,会有很多条可能的直线,但是会有一条最佳的分割线L,如图1.2所示。
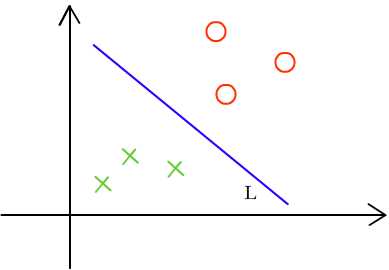
图1.2
绿色的叉叉到L的最短距离为d1,红色圈圈到L的最短距离为d2,保证d1=d2,并且使d1+d2的值最大,那么这条直线就是最佳的分割线。具体的表示如图1.3所示
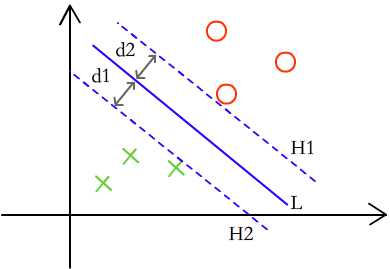
图1.3
图1.3中,蓝色的虚线分别为H1和H2,每一个圈圈和叉叉都可以看成一个向量,落在边缘上的叉叉和圈圈就称为“支持向量”,那么没有在边缘上的向量就是“非支持向量”。
另外,在SVM中,我们经常听到“超平面”的概念。什么是超平面呢?当图中的圈圈和叉叉是二维的时候,那么L就是一条直线;当图中的圈圈和叉叉是三维的时候,那么L就是一个平面;当图中圈圈和叉叉是三维以上的时候,那么L就是一个超平面。
图中的每个圈圈和叉叉都是一个样本,圈圈和叉叉的维数表示样本的特征数量。
二、 怎么用数学描述超平面
如图2.1所示,设超平面L的法向量为,某一样本向量为\[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{u}\],则 在 上的投影为。
对于所有的圈圈样本(正样本),有:
,其中 为正样本向量
对于所有的叉叉样本(负样本),有:
,其中 为负样本向量
图2.1
令 ,可得:
, ①
因为 和 都是未知量,同时缩放 和 对结果无影响,不妨令:
, ②
令 表示第i个样本的分类结果。
对于负样本,令 ,对于正样本, 令 ,结合②中的不等式,可以得到:
好了,目前推到了那么多公式,我们来总结一下,如图2.2所示,
在平面L上的点x满足:
在平面H1上的点x满足:
在平面H2上的点x满足:
图2.2
至此,我们了解了什么是支持向量机,并且完成对超平面的数学描述,下面就是怎样找到这样的一个超平面的问题啦,请见下一篇博文。
标签:
原文地址:http://www.cnblogs.com/ghmgm/p/5615780.html