标签:
和相关分析一样,回归分析也可以描述两个变量间的关系,但二者也有所区别,相关分析可以通过相关系数大小描述变量间的紧密程度,而回归分析更进一步,不仅可以描述变量间的紧密程度,还可以定量的描述当一个变量变化时,对另一个变量的影响程度,这是相关分析无法做到的,正因为如此,回归分析更多用来预测和控制变量值,但是回归分析并不等同于因果关系。
根据模型的不同可以分为线性回归和非线性回归
线性回归分析一般用线性模型来描述,和方差分析模型一样,只是各部分的叫法有所不同,回归模型分为常量、回归部分、残差
常量就是所谓的截距,回归部分由回归系数和自变量组成,这里回归系数也可以成为斜率,残差就是预测值和实测值之间的差,含义为所有不能被自变量估计的随机和非随机因素共同引起的变异。这些概念都和方差分析模型类似。
线性回归也有一定的适用条件
1.线性趋势,即自变量和因变量之间是线性的,这是线性回归最基本的要求,如果不是,则不能用线性回归来分析,这点可以通过散点图来确认
2.独立性,即因变量的取值相互独立,反映到模型中,就是要求残差相互独立
3.正态性,即要求因变量服从正态分布,反映到模型中,就是要求残差残差服从正态分布
4.方差齐性,即要求因变量具有相同的方差,反映到模型中,就是要求残差具有相同的方差
5.自变量之间不能存在高度相关性
以上3,4点会影响因变量的预测值和预测区间,第5点在多个自变量的多重线性回归中要特别加以注意。
只有一个自变量和一个因变量的线性回归称为简单线性回归,本节主要介绍简单线性回归。
分析—回归—线性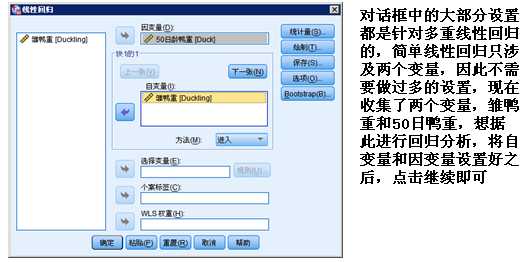
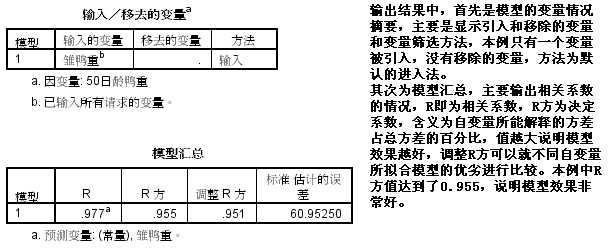
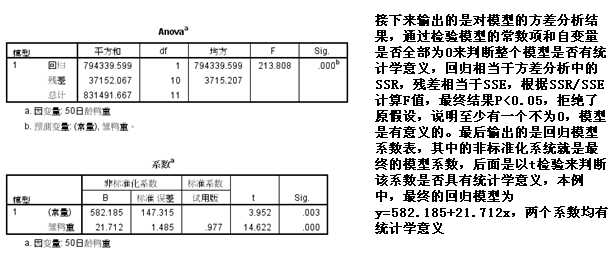
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5617089.html