标签:
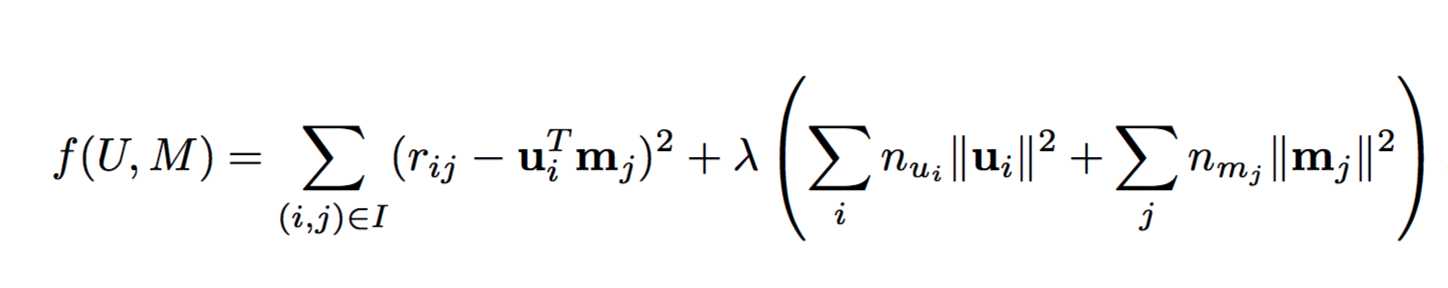
其中,$n_{u_i}$表示用户$i$评分的电影数目,$n_{m_j}$表示对电影$j$评分的用户数目。设$I_i$表示用户$i$所评分的电影集合,则$n_{u_i}$是$I_i$的基数,同样的,$I_j$表示对电影$j$评分的用户集合,$n_{m_j}$是$I_j$的基数。这对应于Tikhonov正则化中的$\Gamma_U=diag(n_{u_i})$和$\Gamma_M=diag(n_{m_j})$
设$U=[\vec{u_i}]$为用户特征矩阵,
我们在$M$给定的情况下来求解$U$。$U$中某一列$u_i$是通过求解一个正则化线性最小二乘问题确定的,该问题的求解需要已知的用户$i$的评分,以及用户$i$参与评分的电影的特征向量$m_j$.
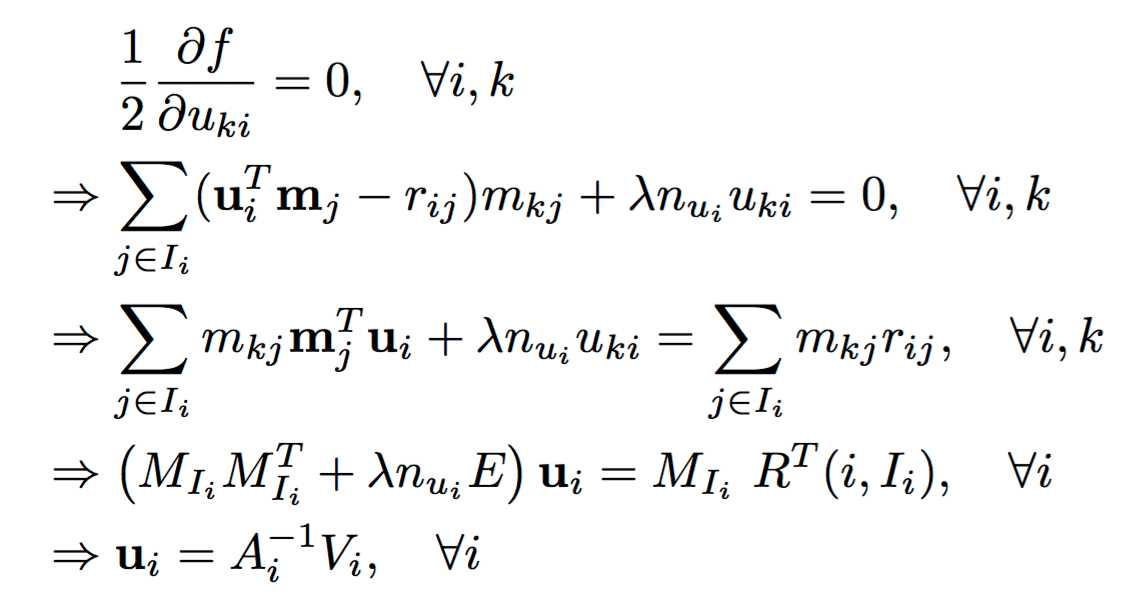
标签:
原文地址:http://www.cnblogs.com/lengyue365/p/5629713.html