傅立叶变换与小波分析

标签：

首先是几个名词：

时域：时域是描述数学函数或物理信号对时间的关系，我们在实际中对信号物理量的描述都是以时间为基准的，沿着时间增加的方向我们才有了波形周期、波形的概念，从以时间为角度称为时域。

频域：频域分析是把信号变为以频率轴为坐标表示出来。也即从频率的角度去描述波形。

时域分析与频域分析是对模拟信号的两个观察面，根据傅立叶分析，所有的波形都可以分解为正弦波，可以由不同频率的正弦波叠加而成，一种频率的正弦波在频域上对应一个点，就行时域上的时间点一样。例如下图波形，从时域上看是类似方波，二如果从频域上看就是一个个线段。

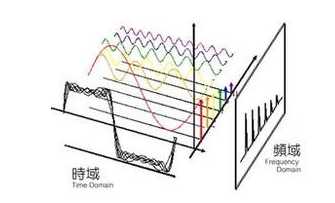
傅立叶变换：将时域上的波形分解成正弦波的过程就是傅立叶变换，傅立叶正变换可以将波形分解，投影到频域上，傅立叶逆变换可以将频域上波形叠加，映射到时域上。变换过程如下图所示：

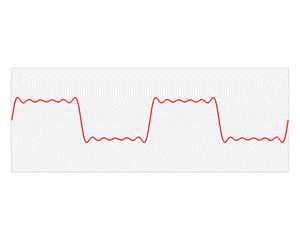
为何要进行傅立叶变换？

很多在时域看似不可能做到的数学操作，在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。离散傅里叶变换（DFT）是傅里叶变换在离散系统中的表示形式。但是DFT的计算量非常大， FFT就是DFT的一种快速算法。

matlab实现：

我们对函数x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)进行FFT变换，并绘制出变换之前和之后的图像。

fs=100;N=1024;n=0:N-1;t=n/fs;
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号函数
subplot(2,1,1),plot(t,x); %绘出信号曲线
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求取Fourier变换的振幅
f=n*fs/N; %求频率
subplot(2,1,2),plot(f,mag); %绘出随频率变化的振幅
xlabel(‘频率/Hz‘);
ylabel(‘振幅‘);title(‘N=1024‘);grid on;

Matlab代码

结果如下，我们可以看出上方是时域波形，下方是频域波形：

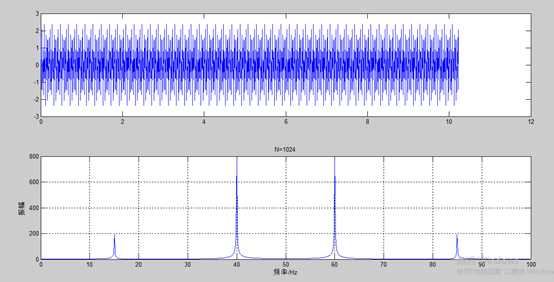
傅立叶变换的缺点：

基于傅里叶(Fourier)变换的信号频域表示,揭示了时间函数和频谱函数之间的内在联系，但是基于傅里叶变换的信号频域表示,揭示了时间函数和频谱函数之间的内在联系。傅里叶变换可以完成从时域到频域的转换(正变换),也可以完成从频域到时域的转换(逆变换),但不能同时具有时域和频域信息。因此后来的小波分析弥补了傅立叶分析不能同时得到时域和频域的缺点。

小波：均值为0的一类波形

小波分析：将原来的信号分解为基于小波波形经过平移和比例变化之后的一系列波形。

傅立叶变换与小波分析

标签：

原文地址：http://www.cnblogs.com/feichangnice/p/5631245.html