标签:
1.几个名词:
神经网络:是一种模仿生物神经网络的运算模型,由大量的节点之间相互联接构成。
传输函数:每个节点代表一种特定的输出函数,称为激励函数,完成对给节点信号的非线性映射,传输函数应该为单值函数,使得神经元是可逆的,常用的传输函数有Sigmoid函数和对数Sigmoid函数。
权重:每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重,权重反应了神经元之间的连接强度,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。
单个神经元:
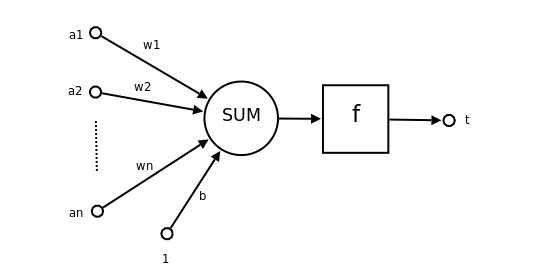

一个神经元的功能是求得输入向量与权向量的内积后,经一个非线性传递函数得到一个标量结果。
单个神经元的作用:把一个n维向量空间用一个超平面分割成两部分(称之为判断边界),给定一个输入向量,神经元可以判断出这个向量位于超平面的哪一边。
该超平面的方程
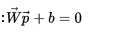

2.神经元网络分类:
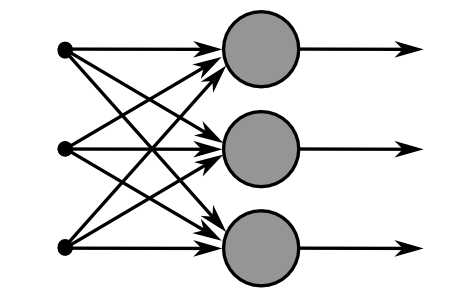
神经网络分为单层和多层
单层神经网络是最基本的神经元网络形式,由有限个神经元构成,所有神经元的输入向量都是同一个向量。由于每一个神经元都会产生一个标量结果,所以单层神经元的输出是一个向量,向量的维数等于神经元的数目,单层神经网络如下图所示:
多层神经网络分为多种,
(1)前馈网络:也称前向网络。这种网络只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号,BP神经网络就属于前馈网络。前馈网络如图所示:
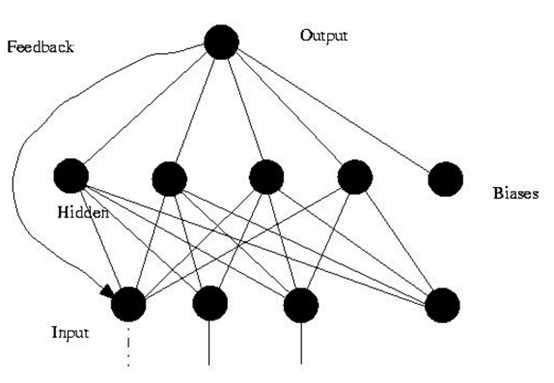
(2)反馈型神经网络:这一种从输出到输入具有反馈连接的神经网络,其结构比前馈网络要复杂得多。典型的反馈型神经网络有:Elman网络和Hopfield网络,反馈网络如图所示:
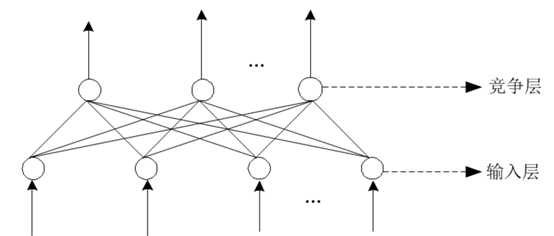
(3)自组织网络 自组织神经网络是一种无导师学习网络,无导师网络如图所示:
3.神经网络训练
自动学习:通过训练样本的校正,对各个层的权重进行校正(learning)而建立模型的过程,称为自动学习过程(training algorithm)。
学习方法:神经网络的学习方法主要包括有导师学习和无导师学习。
无导师学习算法:Hebb学习率
当两个神经元同时处于激发状态时两者间的连接权会被加强,否则被减弱。 为了理解Hebb算法,有必要简单介绍一下条件反射实验。巴甫洛夫的条件反射实验:每次给狗喂食前都先响铃,时间一长,狗就会将铃声和食物联系起来。以后如果响铃但是不给食物,狗也会流口水。
Hebb的理论认为在同一时间被激发的神经元间的联系会被强化。比如,铃声响时一个神经元被激发,在同一时间食物的出现会激发附近的另一个神经元,那么这两个神经元间的联系就会强化,从而记住这两个事物之间存在着联系。相反,如果两个神经元总是不能同步激发,那么它们间的联系将会越来越弱。
有导师学习算法:Delta学习规则
而 delta 规则是基于梯度降落这样一种思路。这个复杂的数学概念可以举个简单的例子来表示。从给定的几点来看,向南的那条路径比向东那条更陡些。向东就像从悬崖上掉下来,但是向南就是沿着一个略微倾斜的斜坡下来,向西像登一座陡峭的山,而北边则到了平地,只要慢慢的闲逛就可以了。所以您要寻找的是到达平地的所有路径中将陡峭的总和减少到最小的路径。在权系数的调整中,神经网络将会找到一种将误差减少到最小的权系数的分配方式。
若神经元实际输出比期望输出大,则减小所有输入为正的连接的权重,增大所有输入为负的连接的权重。反之,若神经元实际输出比期望输出小,则增大所有输入为正的连接的权重,减小所有输入为负的连接的权重。
4.BP神经网络
BP神经网络是典型的有导师学习算法,BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络。它的学习规则是使用梯度下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络的工作过程分为正向传播和反向传播:
正向传播
输入的样本从输入层经过隐单元一层一层进行处理,通过所有的隐层之后,则传向输出层;在逐层处理的过程中,每一层神经元的状态只对下一层神经元的状态产生影响。在输出层把现行输出和期望输出进行比较,如果现行输出不等于期望输出,则进入反向传播过程。
反向传播
反向传播时,把误差信号按原来正向传播的通路反向传回,并对每个隐层的各个神经元的权系数进行修改,以望误差信号趋向最小。
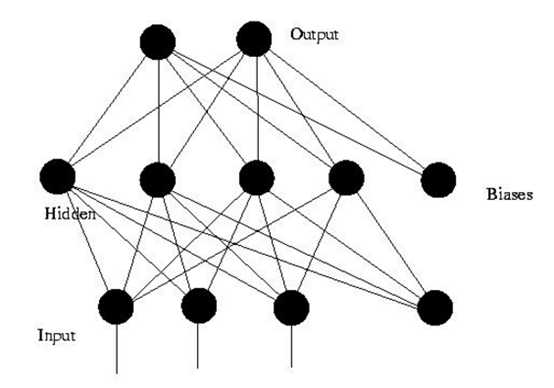
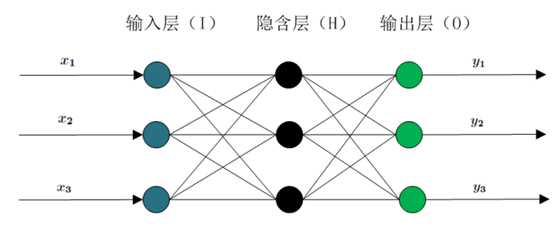
BP神经网络模型拓扑结构包括输入层(input)、隐层(hidden layer)和输出层(output layer),结构如图所示:
BP神经网络的优缺点:
(1)容易形成局部极小值而得不到全局最优值。BP神经网络中极小值比较多,所以很容易陷入局部极小值,这就要求对初始权值和阀值有要求,要使得初始权值和阀值随机性足够好,可以多次随机来实现。
(2)训练次数多使得学习效率低,收敛速度慢。
(3)隐含层的选取缺乏理论的指导。
(4)训练时学习新样本有遗忘旧样本的趋势。
BP神经网络一般用于分类或者逼近问题。如果用于分类,则激活函数一般选用Sigmoid函数或者硬极限函数,如果用于函数逼近,则输出层节点用线性函数。
5.Matlab实现BP神经网络
(1) 什么是归一化?
数据归一化,就是将数据映射到[0,1]或[-1,1]区间或更小的区间,比如(0.1,0.9) 。
(2) 为什么要归一化处理?
<1>输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
<2>数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。
<3>由于神经网络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数,由于S形函数的值域限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
<4>S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(X)在参数a=1时,f(100)与f(5)只相差0.0067。
(3) 归一化算法
一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式:
<1>
y = ( x - min )/( max - min )
其中min为x的最小值,max为x的最大值,输入向量为x,归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间,当激活函数采用S形函数时(值域为(0,1))时这条式子适用。
<2>
y = 2 * ( x - min ) / ( max - min ) - 1
这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数(值域为(-1,1))时这条式子适用。
(4) Matlab数据归一化处理函数
Matlab中归一化处理数据可以采用premnmx , postmnmx , tramnmx 这3个函数。
<1> premnmx
语法:[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
参数:
pn: p矩阵按行归一化后的矩阵
minp,maxp:p矩阵每一行的最小值,最大值
tn:t矩阵按行归一化后的矩阵
mint,maxt:t矩阵每一行的最小值,最大值
作用:将矩阵p,t归一化到[-1,1] ,主要用于归一化处理训练数据集。
<2> tramnmx
语法:[pn] = tramnmx(p,minp,maxp)
参数:
minp,maxp:premnmx函数计算的矩阵的最小,最大值
pn:归一化后的矩阵
作用:主要用于归一化处理待分类的输入数据。
<3> postmnmx
语法: [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)
参数:
minp,maxp:premnmx函数计算的p矩阵每行的最小值,最大值
mint,maxt:premnmx函数计算的t矩阵每行的最小值,最大值
作用:将矩阵pn,tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。
2. 使用Matlab实现神经网络
使用Matlab建立前馈神经网络主要会使用到下面3个函数:
newff :前馈网络创建函数
train:训练一个神经网络
sim :使用网络进行仿真
下面简要介绍这3个函数的用法。
1) newff函数
<1>newff函数语法
newff函数参数列表有很多的可选参数,具体可以参考Matlab的帮助文档,这里介绍newff函数的一种简单的形式。
语法:net = newff ( A, B, {C} ,‘trainFun’)
参数:
A:一个n×2的矩阵,第i行元素为输入信号xi的最小值和最大值;
B:一个k维行向量,其元素为网络中各层节点数;
C:一个k维字符串行向量,每一分量为对应层神经元的激活函数;
trainFun :为学习规则采用的训练算法。
<2>常用的激活函数
常用的激活函数有:
a) 线性函数 (Linear transfer function)
f(x) = x
该函数的字符串为’purelin’。
b) 对数S形转移函数( Logarithmic sigmoid transfer function )
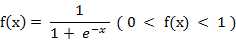
该函数的字符串为’logsig’。
c) 双曲正切S形函数 (Hyperbolic tangent sigmoid transfer function )
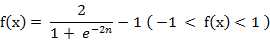
也就是上面所提到的双极S形函数。 该函数的字符串为’ tansig’。
Matlab的安装目录下的toolbox\nnet\nnet\nntransfer子目录中有所有激活函数的定义说明。
<3>常见的训练函数
常见的训练函数有:
traingd :梯度下降BP训练函数(Gradient descent backpropagation)
traingdx :梯度下降自适应学习率训练函数
<4>网络配置参数
一些重要的网络配置参数如下:
net.trainparam.goal :神经网络训练的目标误差
net.trainparam.show : 显示中间结果的周期
net.trainparam.epochs :最大迭代次数
net.trainParam.lr : 学习率
(2) train函数
网络训练学习函数。
语法:[ net, tr, Y1, E ] = train( net, X, Y )
参数:
X:网络实际输入
Y:网络应有输出
tr:训练跟踪信息
Y1:网络实际输出
E:误差矩阵
(3) sim函数
语法:Y=sim(net,X)
参数:
net:网络
X:输入给网络的K×N矩阵,其中K为网络输入个数,N为数据样本数
Y:输出矩阵Q×N,其中Q为网络输出个数
标签:
原文地址:http://www.cnblogs.com/feichangnice/p/5637028.html