Jungle Roads

标签：

Description

The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems. 

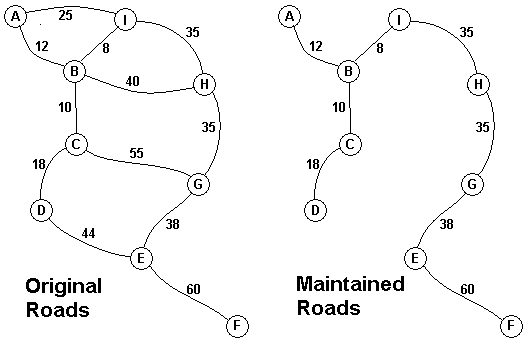
Input

Output

Sample Input

9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0

Sample Output

216
30

题意：所有的桥都坏了，需要重修，每个桥修的时间不一样，求所有的桥都链接上的最短时间。
思路：求的是最小生成树，生成树有两种算法，这边使用Kruskal，其算法思想

假设WN=(V,{E})是一个含有n个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：
先构造一个只含n个顶点，而边集为空的子图，
若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有n棵树的一个森林。
之后，从网的边集E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，
也就是说，将这两个顶点分别所在的两棵树合成一棵树；
反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。
依次类推，直至森林中只有一棵树，也即子图中含有n-1条边为止。

代码：

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int inf = 0x3fffffff;
int p[27];
struct prog {
　　int u;
　　int v;
　　int w;
}mymap[80];
bool cmp ( prog a , prog b)
{
　　return a.w<b.w;
}
int myfind(int x)
{
　　return x==p[x]?x:p[x]=myfind(p[x]);
}
int main()
{
　　int n;
　　while ( cin >> n , n )
　　{
　　　　int i , j ;
　　　　for ( i = 0 ; i < 27 ; i ++ )
　　　　　　p[i] = i ;
　　　　int k = 0 ;
　　　　for ( i = 0 ; i < n - 1 ; i ++ )
　　　　{
　　　　　　char str[3];
　　　　　　int m;
　　　　　　cin >> str >> m ;
　　　　　　for ( j = 0 ; j < m ; j ++ ,k ++ )
　　　　　　{
　　　　　　　　char str2[3];
　　　　　　　　int t;
　　　　　　　　cin >> str2 >> t ;
　　　　　　　　mymap[k].u=(str[0]-‘A‘);
　　　　　　　　mymap[k].v=(str2[0]-‘A‘);
　　　　　　　　mymap[k].w=t;
　　　　　　}
　　　　}

　　　　sort ( mymap , mymap + k , cmp );
　　　　int ans=0;
　　　　for ( i = 0 ; i < k ; i ++ )
　　　　{
　　　　　　int x = myfind(mymap[i].u);
　　　　　　int y = myfind(mymap[i].v);
　　　　　　if( x!=y)
　　　　　　{
　　　　　　　　ans+=mymap[i].w;
　　　　　　　　p[x]=y;
　　　　　　}
　　　　}
　　　　cout<<ans<<endl;
　　}
　　return 0;
}

Jungle Roads

标签：

原文地址：http://www.cnblogs.com/2016zhanggang/p/5637833.html