标签:
067.3 NOIP模拟赛
说明:本次考试3道题3个小时。
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 n 张地毯,编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
输入格式:
输入文件名为carpet.in 。
输入共n+2 行。
第一行,一个整数n ,表示总共有 n 张地毯。
接下来的n 行中,第 i+1 行表示编号i 的地毯的信息,包含四个正整数 a ,b ,g ,k ,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a ,b )以及地毯在x轴和y 轴方向的长度。
第n+2 行包含两个正整数 x 和y,表示所求的地面的点的坐标(x ,y)。
输出格式:
输出文件名为carpet.out 。
输出共1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1 。
【输入样例1】 3 1 0 2 3 0 2 3 3 2 1 3 3 2 2 【输入样例2】 3 1 0 2 3 0 2 3 3 2 1 3 3 4 5
【输出样例1】 3 【输出样例2】 -1
【样例解释1】
如下图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是 3 号地毯。

【数据范围】
对于30% 的数据,有 n ≤2 ;
对于50% 的数据,0 ≤a, b, g, k≤100;
对于100%的数据,有 0 ≤n ≤10,000 ,0≤a, b, g, k ≤100,000。
noip2011提高组day1第1题
太水了,不解释
AC代码:
#include<iostream> using namespace std; #define N 100100 int a[N],b[N],c[N],d[N],k=-1,n,x,y; int main(){ cin>>n; for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i]>>d[i]; cin>>x>>y; for(int i=1;i<=n;i++) if(x-a[i]>=0&&x-a[i]<=c[i]&&y-b[i]>=0&&y-b[i]<=d[i]) k=i; cout<<k<<endl; return 0; }
16 世纪法国外交家 Blaise de Vigenère 设计了一种多表密码加密算法――Vigenère 密
码。Vigenère 密码的加密解密算法简单易用,且破译难度比较高,曾在美国南北战争中为
南军所广泛使用。
在密码学中,我们称需要加密的信息为明文,用 M 表示;称加密后的信息为密文,用
C 表示;而密钥是一种参数,是将明文转换为密文或将密文转换为明文的算法中输入的数据,
记为 k。 在 Vigenère 密码中,密钥 k 是一个字母串,k=k1k2…kn。当明文 M=m1m2…mn时,
得到的密文 C=c1c2…cn,其中 ci=mi®ki,运算®的规则如下表所示:

Vigenère 加密在操作时需要注意:
®运算忽略参与运算的字母的大小写,并保持字母在明文 M 中的大小写形式;
例如,明文 M=Helloworld,密钥 k=abc 时,密文 C=Hfnlpyosnd。

输入格式:
输入共 2 行。
第一行为一个字符串,表示密钥 k,长度不超过 100,其中仅包含大小写字母。第二行
为一个字符串,表示经加密后的密文,长度不超过 1000,其中仅包含大小写字母。
输出格式:
输出共 1 行,一个字符串,表示输入密钥和密文所对应的明文。
CompleteVictory Yvqgpxaimmklongnzfwpvxmniytm
Wherethereisawillthereisaway
【数据说明】
对于 100%的数据,输入的密钥的长度不超过 100,输入的密文的长度不超过 1000,且
都仅包含英文字母。
NOIP 2012 提高组 第一天 第一题
注意点这里,其余问题不大
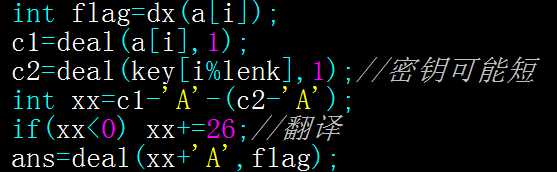
AC代码:
#include<cstdio> #include<cstring> using namespace std; #define N 1024 char key[N],a[N]; inline int dx(char c){//锁定原字母的大小写 if(c>=‘A‘&&c<=‘Z‘)return 1; else if(c>=‘a‘&&c<=‘z‘)return 0; } inline char deal(char c,int i){//处理之后密文的大小写 if(i==1&&c>=‘a‘&&c<=‘z‘)return c-32; else if(i==0&&c>=‘A‘&&c<=‘Z‘)return c+32; else return c; } void action(){ int lena=strlen(a),lenk=strlen(key); char c1,c2,ans; for(int i=0;i<lena;i++){ int flag=dx(a[i]); c1=deal(a[i],1); c2=deal(key[i%lenk],1);//密钥可能短 int xx=c1-‘A‘-(c2-‘A‘); if(xx<0) xx+=26;//翻译 ans=deal(xx+‘A‘,flag); printf("%c",ans); } puts(""); } int main(){ scanf("%s%s",key,a); action(); return 0; }
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个N 行M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入格式:
输入文件的每行中两个数之间用一个空格隔开。输入的第一行是两个正整数N 和M,表示矩形的规模。接下来N 行,每行M 个正整数,依次代表每座城市的海拔高度。
输出格式:
输出有两行。如果能满足要求,输出的第一行是整数1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
【输入样例1】 2 5 9 1 5 4 3 8 7 6 1 2 【输入样例2】 3 6 8 4 5 6 4 4 7 3 4 3 3 3 3 2 2 1 1 2
【输出样例1】 1 1 【输出样例2】 1 3
【样例1 说明】
只需要在海拔为9 的那座城市中建造蓄水厂,即可满足要求。
【样例2 说明】

上图中,在3 个粗线框出的城市中建造蓄水厂,可以满足要求。以这3 个蓄水厂为源头
在干旱区中建造的输水站分别用3 种颜色标出。当然,建造方法可能不唯一。
【数据范围】

这个题有意思,着重讲一下。
闲扯一会儿:
考试的时候思路基本上和题解一样,就连dp方程都一样~~貌似以前看过。
考试的时候,想着bfs比dfs快,结果是bfs->TLE,dfs->AC.那分啊,心疼死我了,tyts。
解题思路:
对于第一行的每个城市,我们可以预处理出在这座城市建立蓄水厂,水流能到达最下面一行的哪些城市;如果最终的题目是有解的,那么最后一行这些被覆盖的城市是连续的,反证:如果水流到达最下面一行的城市是断开不连续的,则说明中间有城市海拔比四周都高,其他城市过来的水流也流不上去,因此永远无法被覆盖,与我们之前的条件相矛盾。
预处理出来每做城市的覆盖范围后,这道题就变成这样:给你长度为m的x轴,现在有m条线段,求覆盖x轴至少要多少根线段。
我们既可以用DP,也可以用贪心,这里采用DP
设,f[i]表示覆盖1~i所需要的最少线段g[j]表示线段i覆盖的区间
则 dp方程:f(i) = min{ f[i] , f[g[j].L - 1] + 1 | i >= g[i].L&&i <= g[i].R }
考试代码:
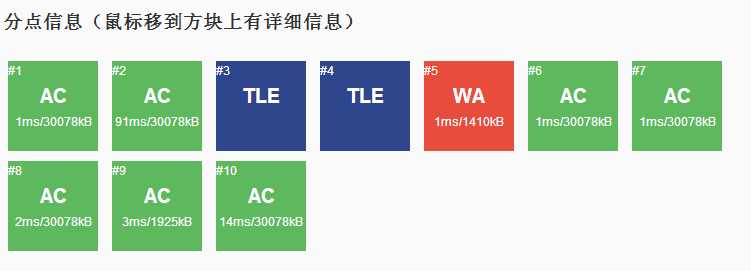
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; #define N 1010 int dx[]={1,0,-1,0}; int dy[]={0,1,0,-1}; int bo[N],vis[N],l[N],r[N],f[N]; struct node{ int x,y,v; }map[N][N]; int n,m; int bfs(int s,int x,int y){ queue<node>que; que.push(map[x][y]); while(!que.empty()){ node h=que.front();que.pop(); for(int i=0;i<4;i++){ int xx=h.x+dx[i],yy=h.y+dy[i]; if(h.v>map[xx][yy].v&&xx>0&&xx<=n&&yy>0&&yy<=m){ que.push(map[xx][yy]); if(xx==n&&!vis[yy]){ vis[yy]=1,bo[yy]++; if(yy<l[s]||!l[s]) l[s]=yy; if(yy>r[s]) r[s]=yy; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&map[i][j].v); map[i][j].x=i;map[i][j].y=j; } } int sum=0,flag=0; for(int i=1;i<=m;i++){ if(i>1&&map[1][i].v<map[1][i-1].v) continue; if(i<m&&map[1][i].v<map[1][i+1].v) continue; memset(vis,0,sizeof(vis)); bfs(i,1,i); } for(int i=1;i<=m;i++){ if(!bo[i]){ flag=1;sum++; } } if(flag){printf("0\n%d\n",sum);return 0;} printf("1\n"); for(int i=1;i<=m;i++){ for(int j=l[i];j<=r[i];j++){ if(f[j]>f[l[i]-1]+1||!f[j]) f[j]=f[l[i]-1]+1; } } printf("%d\n",f[m]); return 0; }
我看了各种题解,都说每个点(i,j)只能搜一遍(为什么只能搜一遍???),改完之后,依然WA,bfs搜不到?

#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; #define N 510 int dx[]={1,0,-1,0}; int dy[]={0,1,0,-1}; int bo[N],vis[N][N],l[N],r[N],f[N]; struct node{ int x,y,v; }map[N][N]; int n,m; int bfs(int s,int x,int y){ queue<node>que; que.push(map[x][y]); while(!que.empty()){ node h=que.front();que.pop(); for(int i=0;i<4;i++){ int xx=h.x+dx[i],yy=h.y+dy[i]; if(!vis[xx][yy]&&h.v>map[xx][yy].v&&xx>0&&xx<=n&&yy>0&&yy<=m){ vis[xx][yy]=1; que.push(map[xx][yy]); if(xx==n){ bo[yy]++; if(yy<l[s]||!l[s]) l[s]=yy; if(yy>r[s]) r[s]=yy; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&map[i][j].v); map[i][j].x=i;map[i][j].y=j; } } int sum=0,flag=0; for(int i=1;i<=m;i++){ if(i>1&&map[1][i].v<map[1][i-1].v) continue; if(i<m&&map[1][i].v<map[1][i+1].v) continue; memset(vis,0,sizeof(vis)); bfs(i,1,i); } for(int i=1;i<=m;i++){ if(!bo[i]){ flag=1;sum++; } } if(flag){printf("0\n%d\n",sum);return 0;} printf("1\n"); for(int i=1;i<=m;i++){ for(int j=l[i];j<=r[i];j++){ if(f[j]>f[l[i]-1]+1||!f[j]) f[j]=f[l[i]-1]+1; } } printf("%d\n",f[m]); return 0; }
AC代码:

dfs便捷版
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; #define N 1010 int dx[]={1,0,-1,0}; int dy[]={0,1,0,-1}; int bo[N],vis[N][N],map[N][N],l[N],r[N],f[N]; int n,m; void dfs(int s,int x,int y){ if(x==n){ bo[y]=1; if(y<l[s]||!l[s]) l[s]=y; if(y>r[s]) r[s]=y; } int h=map[x][y]; vis[x][y]=1; if(x<n&&map[x+1][y]<h&&!vis[x+1][y]) dfs(s,x+1,y); if(x>1&&map[x-1][y]<h&&!vis[x-1][y]) dfs(s,x-1,y); if(y<m&&map[x][y+1]<h&&!vis[x][y+1]) dfs(s,x,y+1); if(y>1&&map[x][y-1]<h&&!vis[x][y-1]) dfs(s,x,y-1); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&map[i][j]); } } int sum=0,flag=0; for(int i=1;i<=m;i++){ if(i>1&&map[1][i]<map[1][i-1]) continue; if(i<m&&map[1][i]<map[1][i+1]) continue; memset(vis,0,sizeof(vis)); dfs(i,1,i); } for(int i=1;i<=m;i++){ if(!bo[i]){ flag=1;sum++; } } if(flag){printf("0\n%d\n",sum);return 0;} printf("1\n"); for(int i=1;i<=m;i++){ for(int j=l[i];j<=r[i];j++){ if(f[j]>f[l[i]-1]+1||!f[j]) f[j]=f[l[i]-1]+1; } } printf("%d\n",f[m]); return 0; }
bfs麻烦版
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; #define N 510 int dx[]={1,0,-1,0}; int dy[]={0,1,0,-1}; int bo[N],vis[N][N],l[N],r[N],f[N]; struct node{ int x,y,v; }map[N][N]; int n,m; int bfs(int s,int x,int y){ queue<node>que; que.push(map[x][y]); while(!que.empty()){ node h=que.front();que.pop(); for(int i=0;i<4;i++){ int xx=h.x+dx[i],yy=h.y+dy[i]; if(!vis[xx][yy]&&h.v>map[xx][yy].v&&xx>0&&xx<=n&&yy>0&&yy<=m){ vis[xx][yy]=1; que.push(map[xx][yy]); if(xx==n){ bo[yy]++; if(yy<l[s]||!l[s]) l[s]=yy; if(yy>r[s]) r[s]=yy; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&map[i][j].v); map[i][j].x=i;map[i][j].y=j; } } int sum=0,flag=0; for(int i=1;i<=m;i++){ if(i>1&&map[1][i].v<map[1][i-1].v) continue; if(i<m&&map[1][i].v<map[1][i+1].v) continue; memset(vis,0,sizeof(vis)); bfs(i,1,i); } for(int i=1;i<=m;i++){ if(!bo[i]){ flag=1;sum++; } } if(flag){printf("%d\n%d\n",n==1?1:0,sum);return 0;}//这里还需要特判n=1时,可能是bfs的缺陷 printf("1\n"); for(int i=1;i<=m;i++){ for(int j=l[i];j<=r[i];j++){ if(f[j]>f[l[i]-1]+1||!f[j]) f[j]=f[l[i]-1]+1; } } printf("%d\n",f[m]); return 0; }
-----------------------------------------------------------------------------------------------------------------------------------------------
华丽的分割线
------------------------------------------------------------------------------------------------------------------------------------------------
反思:1、标志位设错,就会TLE,(考试代码为什么写一维的vis[],白白少了20分);
2、简单搜索时,建议用dfs(至少不用特判(坑爹的出题人,~~~~(>_<)~~~~));
标签:
原文地址:http://www.cnblogs.com/shenben/p/5638010.html