标签:
原题是分别采用线性核和高斯核对西瓜数据集进行SVM的训练,周老师推荐的是LIMSVM,这里我使用的仍然是sklearn。
#!/usr/bin/python # -*- coding:utf-8 -*- import numpy as np import matplotlib.pyplot as plt from sklearn import svm, datasets file1 = open(‘c:\quant\watermelon.csv‘,‘r‘) data = [line.strip(‘\n‘).split(‘,‘) for line in file1] data = np.array(data) X = [[float(raw[-2]), float(raw[-1])] for raw in data[1:,1:-1]] #X = [[float(raw[-3]), float(raw[-2])] for raw in data[1:]] y = [1 if raw[-1]==‘1‘ else 0 for raw in data[1:]] X = np.array(X) y = np.array(y) h = .02 # step size in the mesh # we create an instance of SVM and fit out data. We do not scale our # data since we want to plot the support vectors C = 1000 # SVM regularization parameter svc = svm.SVC(kernel=‘linear‘, C=C).fit(X, y) rbf_svc = svm.SVC(kernel=‘rbf‘, gamma=0.7, C=C).fit(X, y) # create a mesh to plot in x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # title for the plots titles = [‘SVC with linear kernel‘, ‘SVC with RBF kernel‘] for i, clf in enumerate((svc, rbf_svc)): # Plot the decision boundary. For that, we will assign a color to each # point in the mesh [x_min, m_max]x[y_min, y_max]. plt.subplot(1, 2, i + 1) plt.subplots_adjust(wspace=0.4, hspace=0.4) Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # Put the result into a color plot Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) # Plot also the training points plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired) plt.xlabel(‘Sugar content‘) plt.ylabel(‘Density‘) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.xticks(()) plt.yticks(()) plt.title(titles[i]) plt.show()
结果如下:
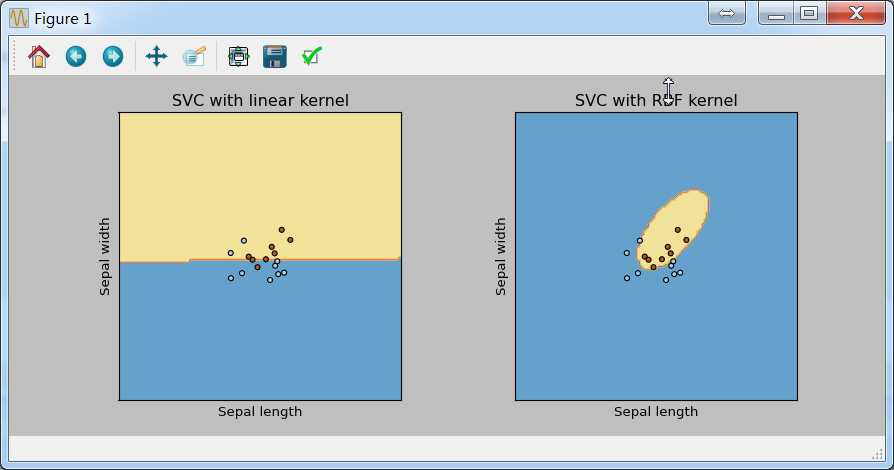
线性核的支持向量也是线性的,高斯核的支持向量是曲线。
标签:
原文地址:http://www.cnblogs.com/zhusleep/p/5639505.html