码迷，mamicode.com
首页 > 其他好文 > 详细

图的遍历 - 数据结构

时间：2016-07-05 06:21:57      阅读：154      评论：0      收藏：0      [点我收藏+]

标签：

图的遍历 - 数据结构 

 

概述

 

图的遍历是指从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作，图的其它算法如求解图的连通性问题，拓扑排序，求关键路径等都是建立在遍历算法的基础之上。

由于图结构本身的复杂性，所以图的遍历操作也较复杂，主要表现在以下四个方面：
① 在图结构中，没有一个“自然”的首结点，图中任意一个顶点都可作为第一个被访问的结点。
② 在非连通图中，从一个顶点出发，只能够访问它所在的连通分量上的所有顶点，因此，还需考虑如何选取下一个出发点以访问图中其余的连通分量。
③ 在图结构中，如果有回路存在，那么一个顶点被访问之后，有可能沿回路又回到该顶点。

④ 在图结构中，一个顶点可以和其它多个顶点相连，当这样的顶点访问过后，存在如何选取下一个要访问的顶点的问题。

图的遍历通常有深度优先搜索和广度优先搜索两种方式，他们对无向图和有向图都适用。

 

1.深度优先搜索

 

深度优先搜索（Depth_Fisrst Search）遍历类似于树的先根遍历，是树的先根遍历的推广。

 假设初始状态是图中所有顶点未曾被访问，则深度优先搜索可从图中某个顶点发v 出发，访问此顶点，然后依次从v 的未被访问的邻接点出发深度优先遍历图，直至图中所有和v 有路径相通的顶点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

以如下图的无向图G5为例，进行图的深度优先搜索：

技术分享

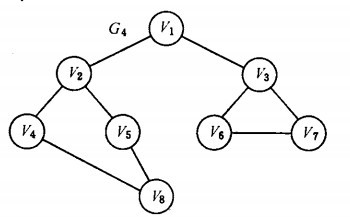
G5

搜索过程：

技术分享

 

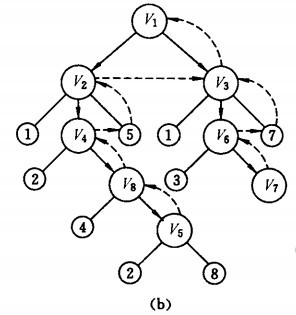
假设从顶点v1 出发进行搜索，在访问了顶点v1 之后，选择邻接点v2。因为v2 未曾访问，则从v2 出发进行搜索。依次类推，接着从v4 、v8 、v5 出发进行搜索。在访问了v5 之后，由于v5 的邻接点都已被访问，则搜索回到v8。由于同样的理由，搜索继续回到v4，v2 直至v1，此时由于v1 的另一个邻接点未被访问，则搜索又从v1 到v3，再继续进行下去由此，得到的顶点访问序列为：

技术分享

 

显然，这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问，需附设访问标志数组visited[0:n-1], ，其初值为FALSE ，一旦某个顶点被访问，则其相应的分量置为TRUE。
1）邻接矩阵的存储方式实现：

 

[cpp] view plain copy
 
 print?
  1. // stdafx.h : include file for standard system include files,  
  2. // or project specific include files that are used frequently, but  
  3. // are changed infrequently  
  4. //  
  5.   
  6. #pragma once  
  7.   
  8. #include "targetver.h"  
  9. #include <stdio.h>    
  10. #include "stdlib.h"  
  11. #include <iostream>  
  12. using namespace std;  
  13.   
  14. //宏定义      
  15. #define TRUE   1      
  16. #define FALSE   0     
  17. #define NULL 0  
  18. #define OK    1      
  19. #define ERROR   0    
  20. #define INFEASIBLE -1      
  21. #define OVERFLOW -2    
  22.   
  23. #define INFINITY   INT_MAX  
  24. #define MAX_VERTEX_NUM 30  
  25.   
  26.   
  27. typedef int Status   ;  
  28. typedef int ElemType ;  
  29. typedef int VrType  ;  
  30. typedef char VertexType  ;  
  31. /************************************************************************/  
  32. /* 数组表示：邻接矩阵数据结构 
  33. */  
  34. /************************************************************************/  
  35.   
  36. typedef struct ArcCell{  
  37.     VrType adj;                         //顶点关系类型，对无权图，0/1表示是否相邻，有权图表示权值  
  38.     ArcCell  *info;                     //弧相关信息的指针  
  39. }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];  
  40.   
  41. typedef struct{  
  42.     VertexType vexs[MAX_VERTEX_NUM];   //顶点向量  
  43.     AdjMatrix arcs;                    //邻接矩阵  
  44.     int vexnum,arcnum;                 //图的当前顶点数和弧数  
  45. }MGraph;  


 

 

[cpp] view plain copy
 
 print?
  1. // Test.cpp : Defines the entry point for the console application.    
  2. //    
  3. #include "stdafx.h"   
  4.   
  5. bool visited[MAX_VERTEX_NUM];  //访问标识  
  6. Status (*VisitFunc) (int v);   //函数变量  
  7. /************************************************************************/  
  8. /*   
  9.     确定顶点v在图G的位置 
  10. */  
  11. /************************************************************************/  
  12. int LocateVex(MGraph G,VertexType v)  
  13. {  
  14.     for(int i = 0; i<G.vexnum; ++i) {  
  15.         if(G.vexs[i] == v) return i;//找到  
  16.     }  
  17.     return -1;//不存在  
  18. }  
  19.   
  20. /************************************************************************/  
  21. /*   
  22.    
  23. */  
  24. /************************************************************************/  
  25. int FirstAdjVex(MGraph G,int v)  
  26. {  
  27.     int i ;  
  28.     for(i = 0; i<G.vexnum; i++)  
  29.         if( G.arcs[v][i].adj ) return i;  
  30.     if(i == (G.vexnum  -1)) return -1;  
  31.     return -1;   
  32.   
  33. }  
  34.   
  35. int NextAdjVex(MGraph G,int v,int w)  
  36. {  
  37.     int i;  
  38.     for( i = w+1; i<G.vexnum; i++)//+1  
  39.         if(G.arcs[v][i].adj) return i;  
  40.     if(i == (G.vexnum  -1)) return -1;  
  41.     return -1;  
  42.   
  43. }  
  44. /************************************************************************/  
  45. /* 
  46.  邻接矩阵的无向图的创建: 
  47.  注释的代码可以动态生成图。 
  48. */  
  49. /************************************************************************/  
  50.   
  51. void CreatUDG(MGraph &G){  
  52.     cout<<"创建邻接矩阵的无向图："<<endl;  
  53.     int i,j,k,w;  
  54.     //G5的存储：  
  55.     G.arcnum = 8;  
  56.     G.vexnum = 9;  
  57.     for(i=0;i<G.vexnum;++i)  
  58.         for(j=0;j<G.vexnum;++j) {  
  59.             G.arcs[i][j].adj=0;  
  60.             G.arcs[i][j].info=NULL;  
  61.         }  
  62.     G.vexs[0] = ‘1‘;  
  63.     G.vexs[1] = ‘2‘;  
  64.     G.vexs[2] = ‘3‘;  
  65.     G.vexs[3] = ‘4‘;  
  66.     G.vexs[4] = ‘5‘;  
  67.     G.vexs[5] = ‘6‘;  
  68.     G.vexs[6] = ‘7‘;  
  69.     G.vexs[7] = ‘8‘;  
  70.   
  71.     G.arcs[0][1].adj = 1;  
  72.     G.arcs[0][1].info = NULL;  
  73.     G.arcs[1][0].adj = 1;  
  74.     G.arcs[1][0].info = NULL;  
  75.   
  76.     G.arcs[1][3].adj = 1;  
  77.     G.arcs[1][3].info = NULL;  
  78.     G.arcs[3][1].adj = 1;  
  79.     G.arcs[3][1].info = NULL;  
  80.   
  81.     G.arcs[3][7].adj = 1;  
  82.     G.arcs[3][7].info = NULL;  
  83.     G.arcs[7][3].adj = 1;  
  84.     G.arcs[7][3].info = NULL;  
  85.   
  86.     G.arcs[7][4].adj = 1;  
  87.     G.arcs[7][4].info = NULL;  
  88.     G.arcs[4][7].adj = 1;  
  89.     G.arcs[4][7].info = NULL;  
  90.   
  91.     G.arcs[4][1].adj = 1;  
  92.     G.arcs[4][1].info = NULL;  
  93.     G.arcs[1][4].adj = 1;  
  94.     G.arcs[1][4].info = NULL;  
  95.   
  96.     G.arcs[0][2].adj = 1;  
  97.     G.arcs[0][2].info = NULL;  
  98.     G.arcs[2][0].adj = 1;  
  99.     G.arcs[2][0].info = NULL;  
  100.   
  101.     G.arcs[2][5].adj = 1;  
  102.     G.arcs[2][5].info = NULL;  
  103.     G.arcs[5][2].adj = 1;  
  104.     G.arcs[5][2].info = NULL;  
  105.   
  106.     G.arcs[5][6].adj = 1;  
  107.     G.arcs[5][6].info = NULL;  
  108.     G.arcs[6][5].adj = 1;  
  109.     G.arcs[6][5].info = NULL;  
  110.   
  111.     G.arcs[6][2].adj = 1;  
  112.     G.arcs[6][2].info = NULL;  
  113.     G.arcs[2][6].adj = 1;  
  114.     G.arcs[2][6].info = NULL;  
  115.     return ;  
  116.     /* 
  117.     char v1,v2; 
  118.     cout<<"请输入无向图顶点个数和边数:"<<endl; 
  119.     cin>>G.vexnum>>G.arcnum; 
  120.     cout<<"请输入"<<G.vexnum<<"个顶点的值:"<<endl; 
  121.     for(i=0;i<G.vexnum;++i) cin>>G.vexs[i]; 
  122.     for(i=0;i<G.vexnum;++i) 
  123.         for(j=0;j<G.vexnum;++j) { 
  124.             G.arcs[i][j].adj=0; 
  125.             G.arcs[i][j].info=NULL; 
  126.         } 
  127.  
  128.         for( k=1;k<=G.arcnum;++k){ 
  129.             cout<<"请输入第"<<k<<"条边的两个顶点值和它们的权重："<<endl; 
  130.             cin>>v1>>v2>>w; 
  131.             i = LocateVex(G,v1);   j=LocateVex(G,v2);  
  132.             G.arcs[i][j].adj=w; 
  133.             G.arcs[j][i]=G.arcs[i][j]; 
  134.         } 
  135.         */  
  136. }  
  137. /************************************************************************/  
  138. /* 有向图邻接矩阵的创建 
  139. */  
  140. /************************************************************************/  
  141. void CreatDG(MGraph &G){  
  142.     int i,j,k,w;  
  143.     char v1,v2;  
  144.     G.arcnum = 8;  
  145.     G.vexnum = 9;  
  146.     cout<<"请输入有向图顶点个数和边数:";  
  147.     cin>> G.vexnum>> G.arcnum;  
  148.     cout<<"请输入"<<G.vexnum<<"个顶点的值:"<<endl;  
  149.     for(i=0;i<G.vexnum;++i) cin>>G.vexs[i];  
  150.     for(i=0;i<G.vexnum;++i)  
  151.         for(j=0;j<G.vexnum;++j) {  
  152.             G.arcs[i][j].adj = 0;  
  153.             G.arcs[i][j].info = NULL;  
  154.         }  
  155.         for( k=1;k<=G.arcnum;++k){  
  156.             cout<<"请输入第"<<k<<"条边的两个顶点值和它们的权重："<<endl;  
  157.             cin>>v1>>v2>>w;  
  158.             i= LocateVex(G,v1);   j = LocateVex(G,v2);   
  159.             G.arcs[i][j].adj = w;  
  160.         }  
  161. }  
  162.   
  163.   
  164. void visitVex(MGraph G, int v){  
  165.     cout<<G.vexs[v]<<" ";  
  166. }  
  167.   
  168. /************************************************************************/  
  169. /*  以V为出发点对图G 进行递归地DFS 搜索 
  170. */  
  171. /************************************************************************/  
  172. void DFS(MGraph G,int v){  
  173.     visited[v] = true;  
  174.     visitVex( G,  v); //访问第v 个顶点  
  175.     for(int w = FirstAdjVex(G,v); w>=0; w = NextAdjVex(G,v,w)){  
  176.         if(!visited[w]) DFS(G,w); //w未访问过，递归DFS搜索  
  177.   
  178.     }  
  179. }  
  180.   
  181. /************************************************************************/  
  182. /*      
  183. 无向图的深度遍历        
  184. */  
  185. /************************************************************************/  
  186. void DFSTraverse(MGraph G){//  
  187.     int v;  
  188.     for( v = 0; v < G.vexnum; ++v) visited[v] = false;  
  189.     for( v = 0; v < G.vexnum; )   
  190.         if(!visited[v]) DFS( G, v); //v未访问过，从vi开始DFS搜索  
  191.         ++v;//不要像书上写的那样，++v放到for语句，这样会导致多出一次访问  
  192.   
  193. }  
  194.   
  195.   
  196. void printMGraph(MGraph G){  
  197.     cout<<"邻接矩阵已经创建，邻接矩阵为："<<endl;  
  198.     for(int i=0;i<G.vexnum;i++){  
  199.         for(int j=0;j<G.vexnum;j++)  
  200.             cout<<G.arcs[i][j].adj<<" ";  
  201.         cout<<endl;  
  202.     }  
  203. }  
  204.   
  205.   
  206. void main(){  
  207.       
  208.     MGraph G;  
  209.   
  210.     CreatUDG(G);  
  211.     printMGraph(G);  
  212.     cout<<"无向图邻接矩阵的深度遍历结果："<<endl;  
  213.     DFSTraverse(G);  
  214. }  

2） 邻接表的表示实现方式

 

 

[cpp] view plain copy
 
 print?
  1. // stdafx.h : include file for standard system include files,  
  2. // or project specific include files that are used frequently, but  
  3. // are changed infrequently  
  4. //  
  5.   
  6. #pragma once  
  7.   
  8. #include "targetver.h"  
  9. #include <stdio.h>    
  10. #include "stdlib.h"  
  11. #include <iostream>  
  12. using namespace std;  
  13.   
  14. //宏定义      
  15. #define TRUE   1      
  16. #define FALSE   0     
  17. #define NULL 0  
  18. #define OK    1      
  19. #define ERROR   0    
  20. #define INFEASIBLE -1      
  21. #define OVERFLOW -2    
  22.   
  23. #define INFINITY   INT_MAX  
  24. #define MAX_VERTEX_NUM 30  
  25.   
  26.   
  27. typedef int Status   ;  
  28. typedef int ElemType ;  
  29. typedef int VrType  ;  
  30. typedef char VertexType  ;  
  31.   
  32. /************************************************************************/  
  33. /*  邻接表示的图数据结构 
  34. */  
  35. /************************************************************************/  
  36. //定义边结点，即表节点  
  37. typedef struct ArcNode   
  38. {  
  39.     int adjvex;             //弧所指的顶点位置  
  40.     ArcNode *nextarc;       //指向下一条弧的指针  
  41. }ArcNode;  
  42.   
  43. //定义顶点节点，即头节点  
  44. typedef struct VNode    
  45. {  
  46.     VertexType data;        //顶点信息  
  47.     ArcNode *firstarc;      //指向第一条依附该顶点的弧的指针  
  48. }VNode,AdjList[MAX_VERTEX_NUM];  
  49.   
  50. //定义无向图     
  51. typedef struct                        
  52. {  
  53.     AdjList vertices;  
  54.     int vexnum,arcnum;   //图的当前顶点数和弧数  
  55. }ALGraph;  

[cpp] view plain copy
 
 print?
  1. // Test.cpp : Defines the entry point for the console application.    
  2. //    
  3. #include "stdafx.h"   
  4.   
  5. bool visited[MAX_VERTEX_NUM];  //访问标识  
  6. Status (*VisitFunc) (int v);   //函数变量  
  7.   
  8.   
  9. /************************************************************************/  
  10. /* 在无向图中添加以m,n为顶点的边 
  11. */  
  12. /************************************************************************/  
  13. void ArcAdd(ALGraph &G,int m,int n){  
  14.   
  15.     ArcNode *p,*h,*q;  
  16.     p = new ArcNode;  
  17.     p->adjvex = m;  
  18.     p->nextarc = NULL;  
  19.     h = q = G.vertices[n].firstarc;  
  20.     if(q == NULL)  
  21.         G.vertices[n].firstarc = p;  
  22.     else {   
  23.         if((p->adjvex)>(q->adjvex)){   
  24.             p->nextarc = q;  
  25.             G.vertices[n].firstarc = p;  
  26.         }  
  27.         else {   
  28.             while( G.vertices[n].firstarc != NULL && q->nextarc != NULL && (p->adjvex)<(q->adjvex)){ //使邻接表中边的数据按大到小排列。    
  29.                 h = q;  
  30.                 q = q->nextarc;  
  31.             }  
  32.             if(q->nextarc == NULL&&(p->adjvex)<(q->adjvex)){    
  33.                 q->nextarc = p;  
  34.             }  
  35.             else {    
  36.                 p->nextarc = q;  
  37.                 h->nextarc = p;  
  38.             }  
  39.         }  
  40.     }  
  41. }  
  42. /************************************************************************/  
  43. /* 
  44. 创建无向图 
  45. */  
  46. /************************************************************************/  
  47. void CreateDG(ALGraph &G){    
  48.     cout<<"请输入顶点个数和边数："<<endl;  
  49.     cin>> G.vexnum>> G.arcnum;  
  50.     cout<<"请输入顶点值:"<<endl;  
  51.     for(int i= 1; i<= G.vexnum; i++) {  
  52.         char t;  
  53.         cin>>t;  
  54.         G.vertices[i].data = t;  
  55.         G.vertices[i].firstarc = NULL;  
  56.     }  
  57.     int m, n;  
  58.     for(int k = 1; k<=G.arcnum; k++){  
  59.         cout<<"请输入第"<<k<<"条边的两个顶点:"<<endl;  
  60.         cin>>m>>n;  
  61.         if(m<= G.vexnum && n <= G.vexnum && m>0 && n>0){  
  62.             ArcAdd(G, m, n);  
  63.             ArcAdd(G, n, m);  
  64.         }  
  65.         else  cout<<"ERROR."<<endl;   
  66.     }  
  67. }  
  68. /************************************************************************/  
  69. /* 打印邻接表的无向图       
  70. */  
  71. /************************************************************************/  
  72. void PrintGraph(ALGraph G)    
  73. {  
  74.     cout<<"无向图的创建完成,该图的邻接表表示为:"<<endl;  
  75.     ArcNode *p;  
  76.     for(int i=1; i<=G.vexnum; i++)  
  77.     {  
  78.         if(G.vertices[i].firstarc == NULL)  
  79.             cout<<i<<G.vertices[i].data<<"-->NULL"<<endl;  
  80.         else   
  81.         {  
  82.             p = G.vertices[i].firstarc;  
  83.             cout<<i<<G.vertices[i].data<<"-->";  
  84.             while(p->nextarc!=NULL)  
  85.             {  
  86.                 cout<<p->adjvex<<"-->";  
  87.                 p = p->nextarc;  
  88.             }  
  89.             cout<<p->adjvex<<"-->NULL"<<endl;  
  90.         }  
  91.     }  
  92. }  
  93.   
  94.   
  95. /************************************************************************/  
  96. /*     返回v的第一个邻接顶点。若顶点在G中没有邻接表顶点，则返回“空”。    
  97. */  
  98. /************************************************************************/  
  99. int FirstAdjVex(ALGraph G,int v)  
  100. {   
  101.     if(G.vertices[v].firstarc)  
  102.         return G.vertices[v].firstarc->adjvex;  
  103.     else  
  104.         return NULL;  
  105. }  
  106. /************************************************************************/  
  107. /*    
  108.   返回v的（相对于w的）下一个邻接顶点。若w是v的最后一个邻接点，则返回“回”。 
  109. */  
  110. /************************************************************************/  
  111. int NextAdjVex(ALGraph G,int v,int w)     
  112. {  
  113.     ArcNode *p;  
  114.     if(G.vertices[v].firstarc==NULL)  
  115.         return NULL;  
  116.     else {  
  117.         p = G.vertices[v].firstarc;  
  118.         while(p->adjvex!=w) p = p->nextarc;  
  119.   
  120.         if(p->nextarc == NULL) return NULL;  
  121.         else  return p->nextarc->adjvex;  
  122.     }  
  123. }  
  124.   
  125.   
  126.   
  127. void visitVex(ALGraph G, int v){  
  128.     cout<<G.vertices[v].data<<" ";  
  129. }  
  130.   
  131. /************************************************************************/  
  132. /*      
  133. 无向图的深度遍历        
  134. */  
  135. /************************************************************************/  
  136. //从第v个顶点出发递归地深度优先遍历图G  
  137. void DFS(ALGraph G,int v)  
  138. {  
  139.     visited[v] = true;  
  140.     visitVex(G, v);  
  141.     for(int w = FirstAdjVex(G,v);w >= 1; w = NextAdjVex(G,v,w))  
  142.         if(!visited[w]) DFS(G,w);  
  143. }  
  144. //对图G作深度优先遍历  
  145. void DFSTraverse(ALGraph G)  
  146. {   
  147.     for(int v = 1; v <= G.vexnum; v++) visited[v]=false;  
  148.     for(int m = 1; m <= G.vexnum; m++)  
  149.         if(!visited[m]) DFS(G,m);  
  150. }  
  151.   
  152. void main(){  
  153.     ALGraph G;  
  154.     CreateDG(G);  
  155.     PrintGraph(G);  
  156.     DFSTraverse(G);  
  157. }  

 


分析上述算法，在遍历时，对图中每个顶点至多调用一次DFS 函数，因为一旦某个顶点被标志成已被访问，就不再从它出发进行搜索。因此，遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。当用二维数组表示邻接矩阵图的存储结构时，查找每个顶点的邻接点所需时间为O(n2) ，其中n 为图中顶点数。而当以邻接表作图的存储结构时，找邻接点所需时间为O(e)，其中e 为无向图中边的数或有向图中弧的数。由此，当以邻接表作存储结构时，深度优先搜索遍历图的时间复杂度为O(n+e) 。

 

2.广度优先搜索

广度优先搜索（Breadth_First Search） 遍历类似于树的按层次遍历的过程。

 

假设从图中某顶点v 出发，在访问了v 之后依次访问v 的各个未曾访问过和邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。换句话说，广度优先搜索遍历图的过程中以v 为起始点，由近至远，依次访问和v 有路径相通且路径长度为1,2,…的顶点。

对图如下图所示无向图G5 进行广度优先搜索遍历：

技术分享

 

广度搜索过程：

技术分享

首先访问v1 和v1 的邻接点v2 和v3，然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7，最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，由些完成了图的遍历。得到的顶点访问序列为：

 

v1→v2 →v3 →v4→ v5→ v6→ v7 →v8

和深度优先搜索类似，在遍历的过程中也需要一个访问标志数组。并且，为了顺次访问路径长度为2、3、…的顶点，需附设队列以存储已被访问的路径长度为1、2、… 的顶点。

实现：

 

[cpp] view plain copy
 
 print?
  1. // stdafx.h : include file for standard system include files,  
  2. // or project specific include files that are used frequently, but  
  3. // are changed infrequently  
  4. //  
  5.   
  6. #pragma once  
  7.   
  8. #include <stdio.h>    
  9. #include "stdlib.h"  

[cpp] view plain copy
 
 print?
  1. // func.h :  
  2. #pragma once  
  3.   
  4. #include <iostream>  
  5. using namespace std;  
  6.   
  7. //宏定义      
  8. #define TRUE   1      
  9. #define FALSE   0     
  10. #define NULL 0  
  11. #define OK    1      
  12. #define ERROR   0    
  13. #define INFEASIBLE -1      
  14. #define OVERFLOW -2    
  15.   
  16. #define INFINITY   INT_MAX  
  17. #define MAX_VERTEX_NUM 30  
  18.   
  19.   
  20. typedef int Status   ;  
  21. typedef int ElemType ;  
  22. typedef int VrType  ;  
  23. typedef char VertexType  ;  
  24.   
  25. /************************************************************************/  
  26. /*  邻接表示的图数据结构 
  27. */  
  28. /************************************************************************/  
  29. //定义边结点  
  30. typedef struct ArcNode   
  31. {  
  32.     int adjvex;             //弧所指的顶点位置  
  33.     ArcNode *nextarc;       //指向下一条弧的指针  
  34. }ArcNode;  
  35.   
  36. //定义顶点结点  
  37. typedef struct VNode    
  38. {  
  39.     VertexType data;        //顶点信息  
  40.     ArcNode *firstarc;      //指向第一条依附该顶点的弧的指针  
  41. }VNode,AdjList[MAX_VERTEX_NUM];  
  42.   
  43. //定义无向图     
  44. typedef struct                        
  45. {  
  46.     AdjList vertices;  
  47.     int vexnum,arcnum;   //图的当前顶点数和弧数  
  48. }ALGraph;  
  49.   
  50.   
  51. /************************************************************************/  
  52. /* 需要                                                                     */  
  53. /************************************************************************/  
  54. typedef struct node //定义结点  
  55. {  
  56.     char data;  
  57.     node *next;  
  58. }*Link;  
  59.   
  60. typedef struct //定义链表  
  61. {  
  62.     Link head,tail;  
  63.     int len;  
  64. }Queue;  
  65.   
  66. /************************************************************************/  
  67. /* 构造一个带头结点和尾结点的空的线性链表队列Q 
  68. */  
  69. /************************************************************************/  
  70. Status InitQueue(Queue &Q)  
  71. {  
  72.     Q.head = new node;  
  73.     Q.head->next = Q.tail = new node;  
  74.     Q.tail->next = NULL;  
  75.     Q.len = 0;  
  76.     return 0;  
  77. }  
  78.   
  79. /************************************************************************/  
  80. /*  
  81.  //在线性链表的队列L的结尾添加一个结点 
  82. */  
  83. /************************************************************************/  
  84.  void EnQueue(Queue &Q,int e)  
  85. {  
  86.     Link q = new node;  
  87.     Q.tail->next = q;  
  88.     Q.tail->data = e;  
  89.     Q.tail = q;  
  90.     Q.tail->next = NULL;  
  91.     Q.len++;  
  92. }  
  93. /************************************************************************/  
  94. /* 出列，并将出列的元素值用e返回 
  95. */  
  96. /************************************************************************/  
  97. void DeleteQueue(Queue &Q,int &e)  
  98. {  
  99.     if(Q.head->next == Q.tail) {  
  100.         cout<<"队列为空"<<endl;  
  101.         e = NULL;  
  102.     } else {  
  103.         Link p,q;  
  104.         p = Q.head->next;  
  105.         q = p->next;  
  106.         Q.head->next = q;  
  107.         e = p->data;  
  108.         delete p;  
  109.         Q.len--;  
  110.     }  
  111. }  

[cpp] view plain copy
 
 print?
  1. // Test.cpp : Defines the entry point for the console application.    
  2. //    
  3. #include "stdafx.h"   
  4. #include "func.h"  
  5. bool visited[MAX_VERTEX_NUM];  //访问标识  
  6. Status (*VisitFunc) (int v);   //函数变量  
  7.   
  8. /************************************************************************/  
  9. /* 在无向图中添加以m,n为顶点的边 
  10. */  
  11. /************************************************************************/  
  12. void ArcAdd(ALGraph &G,int m,int n){  
  13.   
  14.     ArcNode *p,*h,*q;  
  15.     p = new ArcNode;  
  16.     p->adjvex = m;  
  17.     p->nextarc = NULL;  
  18.     h = q = G.vertices[n].firstarc;  
  19.     if(q == NULL)  
  20.         G.vertices[n].firstarc = p;  
  21.     else {   
  22.         if((p->adjvex)>(q->adjvex)){   
  23.             p->nextarc = q;  
  24.             G.vertices[n].firstarc = p;  
  25.         }  
  26.         else {   
  27.             while( G.vertices[n].firstarc != NULL && q->nextarc != NULL && (p->adjvex)<(q->adjvex)){   
  28.                 //使邻接表中边的数据按大到小排列。    
  29.                 h = q;  
  30.                 q = q->nextarc;  
  31.             }  
  32.             if(q->nextarc == NULL&&(p->adjvex)<(q->adjvex)){    
  33.                 q->nextarc = p;  
  34.             }  
  35.             else {    
  36.                 p->nextarc = q;  
  37.                 h->nextarc = p;  
  38.             }  
  39.         }  
  40.     }  
  41. }  
  42. /************************************************************************/  
  43. /* 
  44. 创建无向图 
  45. */  
  46. /************************************************************************/  
  47. void CreateDG(ALGraph &G){    
  48.     cout<<"请输入顶点个数和边数："<<endl;  
  49.     cin>> G.vexnum>> G.arcnum;  
  50.     cout<<"请输入顶点值:"<<endl;  
  51.     for(int i= 1; i<= G.vexnum; i++) {  
  52.         char t;  
  53.         cin>>t;  
  54.         G.vertices[i].data = t;  
  55.         G.vertices[i].firstarc = NULL;  
  56.     }  
  57.     int m, n;  
  58.     for(int k = 1; k<=G.arcnum; k++){  
  59.         cout<<"请输入第"<<k<<"条边的两个顶点:"<<endl;  
  60.         cin>>m>>n;  
  61.         if(m<= G.vexnum && n <= G.vexnum && m>0 && n>0){  
  62.             ArcAdd(G, m, n);  
  63.             ArcAdd(G, n, m);  
  64.         }  
  65.         else  cout<<"ERROR."<<endl;   
  66.     }  
  67. }  
  68.   
  69. /************************************************************************/  
  70. /* 打印邻接表的无向图       
  71. */  
  72. /************************************************************************/  
  73. void PrintGraph(ALGraph G)    
  74. {  
  75.     cout<<"无向图的创建完成,该图的邻接表表示为:"<<endl;  
  76.     ArcNode *p;  
  77.     for(int i=1; i<=G.vexnum; i++)  
  78.     {  
  79.         if(G.vertices[i].firstarc == NULL)  
  80.             cout<<i<<G.vertices[i].data<<"-->NULL"<<endl;  
  81.         else   
  82.         {  
  83.             p = G.vertices[i].firstarc;  
  84.             cout<<i<<G.vertices[i].data<<"-->";  
  85.             while(p->nextarc!=NULL)  
  86.             {  
  87.                 cout<<p->adjvex<<"-->";  
  88.                 p = p->nextarc;  
  89.             }  
  90.             cout<<p->adjvex<<"-->NULL"<<endl;  
  91.         }  
  92.     }  
  93. }  
  94.   
  95. /************************************************************************/  
  96. /*     返回v的第一个邻接顶点。若顶点在G中没有邻接表顶点，则返回“空”。    
  97. */  
  98. /************************************************************************/  
  99. int FirstAdjVex(ALGraph G,int v)  
  100. {   
  101.     if(G.vertices[v].firstarc)  
  102.         return G.vertices[v].firstarc->adjvex;  
  103.     else  
  104.         return NULL;  
  105. }  
  106. /************************************************************************/  
  107. /*    
  108.   返回v的（相对于w的）下一个邻接顶点。若w是v的最后一个邻接点，则返回“回”。 
  109. */  
  110. /************************************************************************/  
  111. int NextAdjVex(ALGraph G,int v,int w)     
  112. {  
  113.     ArcNode *p;  
  114.     if(G.vertices[v].firstarc==NULL)  
  115.         return NULL;  
  116.     else {  
  117.         p = G.vertices[v].firstarc;  
  118.         while(p->adjvex!=w) p = p->nextarc;  
  119.   
  120.         if(p->nextarc == NULL) return NULL;  
  121.         else  return p->nextarc->adjvex;  
  122.     }  
  123. }  
  124.   
  125. void visitVex(ALGraph G, int v){  
  126.     cout<<G.vertices[v].data<<" ";  
  127. }  
  128.   
  129. /************************************************************************/  
  130. /*      
  131. 广度优先遍历图G 
  132. */  
  133. /************************************************************************/  
  134.   
  135. void BFSTraverse(ALGraph G)  
  136. {  
  137.     Queue Q;  
  138.     int u;  
  139.     for(int m=1; m<= G.vexnum; m++) visited[m] = false;  
  140.     InitQueue(Q);//借助辅助队列。  
  141.     for(int v=1;v<=G.vexnum;v++)  
  142.         if(!visited[v]) {  
  143.             visited[v]=true;  
  144.             visitVex(G,v);  
  145.             EnQueue(Q,v);  
  146.             while(Q.len!=0)  
  147.             {  
  148.                 DeleteQueue(Q,u);  
  149.                 for(int w=FirstAdjVex(G,u);w>=1;w=NextAdjVex(G,u,w))  
  150.                     if(!visited[w])  
  151.                     {  
  152.                         visited[w]=true;  
  153.                         visitVex(G,v);  
  154.                         EnQueue(Q,w);  
  155.                     }  
  156.             }  
  157.         }  
  158.         cout<<endl;  
  159. }  
  160.   
  161. void main(){  
  162.     ALGraph G;  
  163.     CreateDG(G);  
  164.     PrintGraph(G);  
  165.     cout<<"广度优先搜索的结果为:"<<endl;  
  166.     BFSTraverse(G);  
  167. }  

 


分析上述算法，每个顶点至多进一次队列。遍历图的过程实质是通过边或弧找邻接点的过程，因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同，两者不同之处仅仅在于对顶点访问的顺序不同。

图的遍历 - 数据结构

标签：

原文地址：http://www.cnblogs.com/destim/p/5642214.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！