标签:
这题的关键在于推公式。
推出公式并化简后,中等和困难都可以做了。
之前推了一个公式:
for(int i=1;i<n;i++) for(int j=1;j<m;j++) { if( __gcd(i,j) == 1 ) { ans += 2*(min(i,n-i)*(m-j)+min(j,m-j)*(n-i)-min(i,n-i)*min(j,m-j)); } }
然后做中等难度的时候用容斥来了一发。
妹的,为了n^2维护前缀花了接近一天。。。

int sum[N]; memset(sum,0,sizeof(sum)); for(int n=2;n<N;n++) { for(int m=2;m<N;m++) { dpM[n][m] = dpM[n-1][m]+dpM[n][m-1]-dpM[n-1][m-1]; if(__gcd(n-1,m-1)==1) dpM[n][m]++,dpR[n][m]++,dpL[n][m]++,dp[n][m]++; dpR[n][m]+=dpR[n][m-1]+dpM[n][m-1]+dpM[n-1][m]-dpM[n-1][m-1]; dpL[n][m]+=dpL[n-1][m]+dpM[n-1][m]-dpM[(n+1)/2][m]+dpM[n][m-1]-dpM[n-1][m-1]; dp[n][m] += dpR[n][m-1]-dpR[n-1][m-1]+dpM[n][m-1]-dpM[n-1][m-1]+dp[n-1][m]+dpR[n-1][m]-dpR[(n+1)/2][m]; } } //真是他妈简单 memset(dpR,0,sizeof(dpR)); for(int n=2;n<N;n++) for(int m=2;m<N;m++) { if(__gcd(n-1,m-1)==1) dpR[n][m]++,_dp[n][m]++; dpR[n][m]+=dpR[n][m-1]+dpM[n][m-1]-dpM[n][(m+1)/2]+dpM[n-1][m]-dpM[n-1][m-1]; _dp[n][m]+=_dp[n][m-1]+dpL[n][m-1]-dpL[n][(m+1)/2]+_dp[n-1][m]+dpR[n-1][m]-dpR[(n+1)/2][m] - (_dp[n-1][m-1]+dpL[n-1][m-1]-dpL[n-1][(m+1)/2]+dpR[n-1][m-1]-dpR[(n+1)/2][m-1]+(dpM[n-1][m-1]-dpM[(n+1)/2][m-1]-dpM[n-1][(m+1)/2]+dpM[(n+1)/2][(m+1)/2])); }
其实公式可以化简为:
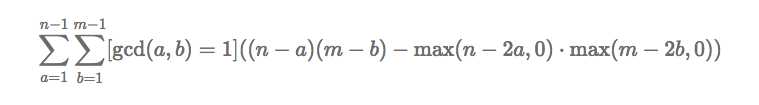
这样子,用二维dp就很好搞了。
然后之前我也推了一种比较简单的递推做普通难度。
// // main.cpp // jisuanke11166.1 // // Created by New_Life on 16/7/4. // Copyright © 2016年 chenhuan001. All rights reserved. // #include <iostream> #include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int dp[4001][4001]; int dp1[4001][4001]; #define MOD (1<<30) int main(int argc, const char * argv[]) { //打个表试试 //随便搞搞 for(int i=1;i<=4000;i++) for(int j=1;j<=4000;j++) { dp1[i][j] = dp1[i-1][j]+dp1[i][j-1]-dp1[i-1][j-1]; dp1[i][j] = (dp1[i][j]%MOD+MOD)%MOD; int flag=0; if(__gcd(i,j) == 1) flag = 1; if(flag) dp1[i][j]++; dp[i][j] += ((dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1])%MOD+dp1[i][j]-dp1[(i)/2][(j)/2])%MOD; dp[i][j] = ((dp[i][j])%MOD+MOD)%MOD; } int T; cin>>T; while(T--) { int ans=0; int n,m; scanf("%d%d",&n,&m); printf("%d\n",(n+m+2*dp[n-1][m-1])%MOD); } return 0; }
对于困难难度。有了上面的那个公式,就是标准的莫比乌斯反演了。
建议先搞懂bzoj2301,然后想想就能想到

// // main.cpp // jisuanke11167 // // Created by New_Life on 16/7/6. // Copyright © 2016年 chenhuan001. All rights reserved. // #include <iostream> #include <stdio.h> #include <string.h> #include <vector> #include <algorithm> using namespace std; #define N 400040 #define MOD (1<<30) //--莫比乌斯反演函数--// //说明:利用线性素数筛选顺便求了个mu //注释部分为求从区间[1,b]和区间[1,d]中取两个数,互质对数O(n^0.5) //复杂度:O(n) int mu[N]; long long sum[3][N]; void mobus() { bool mark[N]; int prime[N]; int pcnt=0; memset(mark,0,sizeof(mark)); mu[1] = 1; for(int i=2;i<N;i++) { if(mark[i] == 0) { prime[pcnt++] = i; mu[i] = -1; } for(int j=0;j<pcnt && i*prime[j]<N;j++) { int tmp = i*prime[j]; mark[tmp] = 1; if( i%prime[j] == 0 ) { mu[tmp] = 0; break; } mu[tmp] = mu[i]*-1; } } for(int i=1;i<N;i++) { sum[0][i] += sum[0][i-1]+mu[i]; sum[1][i] += sum[1][i-1]+mu[i]*i; sum[2][i] += sum[2][i-1]+(long long)mu[i]*i*i; sum[2][i]%=MOD; } } long long gaobili(int b,int d,int nn,int mm,int flag) { if(b<=0||d<=0) return 0; int m = min(b,d); long long ans = 0; long long ans1 = 0; long long ans2 = 0; long long ans3 = 0; while(m>=1) { int tb = b/( b/m +1 )+1; int td = d/( d/m +1 )+1; //前进的最大位置 int tm = max(tb,td); ans =( ans + (long long)(sum[0][m]-sum[0][tm-1])*(b/m)*(d/m) )%MOD; ans1 = (ans1 + (long long)(sum[1][m]-sum[1][tm-1])*(d/m)%MOD*((b/m+1)*(b/m)/2) )%MOD; ans2 = (ans2 + (long long)(sum[1][m]-sum[1][tm-1])*(b/m)%MOD*((d/m+1)*(d/m)/2) )%MOD; ans3 = (ans3 + (long long)(sum[2][m]-sum[2][tm-1])*(((d/m)*(d/m+1)/2)%MOD)%MOD*(((b/m)*(b/m+1)/2))%MOD)%MOD; m = tm-1; } return (ans*nn*mm)%MOD - (ans1*mm*flag)%MOD - (ans2*nn*flag)%MOD + ans3*flag*flag; } int main() { mobus(); int T; cin>>T; while(T--) { int n,m; scanf("%d%d",&n,&m); long long ans = 2*gaobili(n-1, m-1,n,m,1); ans %= MOD; ans -= 2*gaobili((n-1)/2, (m-1)/2,n,m,2); ans += (n+m); ans %= MOD; ans = (ans+MOD)%MOD; cout<<ans<<endl; } return 0; } /* 4 2 2 7 10 23 34 100 100 */
这题从简单到困难,写了至少5,6个版本的代码。为了搞懂莫比乌斯根号n的优化,又去a了几道题。真是弱。真是可悲。
标签:
原文地址:http://www.cnblogs.com/chenhuan001/p/5648300.html