图像的纹理特征之灰度共生矩阵

时间：2016-07-07 00:50:44 阅读：537 评论：0 收藏：0 [点我收藏+]

标签：

（黑灯瞎火好干事。。。。。。。来源一）

由于纹理是由灰度分布在空间位置上反复出现而形成的，因而在图像空间中相隔某距离的两象素之间会存在一定的灰度关系，即图像中灰度的空间相关特性。灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法。

Gray-level co-occurrence matrix from an image

图像的灰度共生矩阵

灰度共生矩阵是像素距离和角度的矩阵函数，它通过计算图像中一定距离和一定方向的两点灰度之间的相关性，来反映图像在方向、间隔、变化幅度及快慢上的综合信息。

使用方法：
glcm = graycomatrix(I)
glcms = graycomatrix(I,param1,val1,param2,val2,...)
[glcms,SI] = graycomatrix(...)

描述：
glcms = graycomatrix(I) 产生图像I的灰度共生矩阵GLCM。它是通过计算两灰度值在图像I中水平相邻的次数而得到的 (也不必是水平相邻的次数，这一参数是可调的，可能通过Offsets来进行调整，比如[0 D]代表是水平方向，[-D D]代表是右上角45度方向，[-D 0]代表是竖直方向，即90度方向，而[-D -D]则代表是左上角，即135度方向），GLCM中的每一个元素（i,j）代表灰度i与灰度j在图像中水平相邻的次数。

因为动态地求取图像的GLCM区间代价过高，我们便首先将灰度值转换到I的灰度区间里。如果I是一个二值图像，那么灰度共生矩阵就将图像转换到两级。如果I是一个灰度图像，那将转换到8级。灰度的级数决定了GLCM的大小尺寸。你可以通过设定参数“NumLevels”来指定灰度的级数，还可以通过设置“GrayLimits"参数来设置灰度共生矩阵的转换方式。

下图显示了如何求解灰度共生矩阵，以（1，1）点为例，GLCM（1，1）值为1说明只有一对灰度为1的像素水平相邻。GLCM（1，2）值为2，是因为有两对灰度为1和2的像素水平相邻。

技术分享

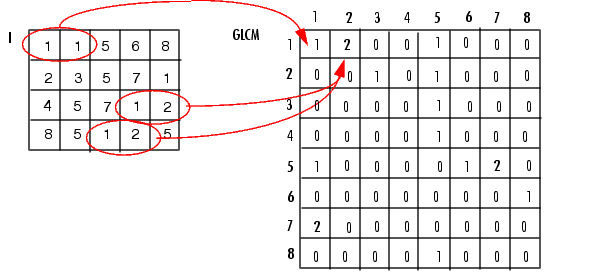
（这里添几句废话，左边是你灰度分级后的图像，右边是你按照八级来的统计矩阵

glcms = graycomatrix(I,param1,val1,param2,val2,...) 返回一个或多个灰度灰度共生矩阵，根据指定的参数。参数可以很简短，并且对大小写不敏感。

参数

‘GrayLimits‘ 是两个元素的向量，表示图像中的灰度映射的范围，如果其设为[]，灰度共生矩阵将使用图像I的最小及最大灰度值作为GrayLimits

‘NumLevels‘   一个整数，代表是将图像中的灰度归一范围。举例来说，如果NumLevels为8，意思就是将图像I的灰度映射到1到8之间，它也决定了灰度共生矩阵的大小

‘Offset‘   上面有解释，是一个p*2的整数矩阵，D代表是当前像素与邻居的距离，通过设置D值，即可设置角度
Angle        Offset
0              [0 D]
45             [-D D]
90             [-D 0]
135            [-D -D]
设置参数的时候offset,偏移量，在此基础上，0表示相邻水平，45表示相邻斜上方，90表示相邻上下，135同理

..................glcm = graycomatrix(I)
      从图像I创建灰度共生矩阵glcm。通过计算具有灰度级i和灰度级j的像素对在水平方向相邻出现的频繁程度。glcm中的每个元素说明了水平方向相邻像素对出现的次数。如果灰度级为L则glcm的维数为L*L。
      2.glcms = graycomatrix(I,param1,val1,param2,val2,...)
根据参数对的设定，返回一个或多个灰度共生矩阵。
      参数说明：
      ‘GrayLimits‘：灰度界限，为二元向量[low high]。灰度值小于等于low 时对应1，大于等于high时对应于灰度级。如果参数设为[]，则共生矩阵使用图像的最小和最大灰度值作为界限，即[min(I(:)) max(I(:))]。
      ‘NumLevels‘：整数，说明I中进行灰度缩放的灰度级数目。例如，如果NumLevel设为8，则共生矩阵缩放I中的灰度值使它们为1到8之间的整数。灰度级的数目决定了共生矩阵glcm的尺寸。缺省情况：数字图像：8；二进制图像：2。
      ‘Offset‘：p行2列整型矩阵，说明感兴趣像素与其相邻像素之间的距离。每行是一个说明像素对之间偏移关系的二元向量[row_offset, col_offset]。行偏移row_offset是感兴趣像素和其相邻像素之间的间隔行数。列偏移同理。偏移常表达为一个角度，常用的角度如下：（其中D为像素距离）
      角度    0          45       90       135
      Offset [0,D]    [-D D] [-D 0]    [-D -D]
      3.[glcms,SI] = graycomatrix(...)
      返回缩放图像SI，SI是用来计算灰度共生矩阵的。SI中的元素值介于1和灰度级数目之间。
graycoprops：得到灰度共生矩阵得到各种属性
      stats = graycoprops(glcm, properties)：从灰度共生矩阵glcm计算静态属性。glcm是m*n*p的有效灰度共生矩阵。如果glcm是一个灰度共生矩阵的矩阵，则stats是包括每个灰度共生矩阵静态属性的矩阵。
      graycoprops正规化了灰度共生矩阵，因此元素之和为1。正规化的GLCM中的元素（r，c）是具有灰度级r和c的定义的空间关系的像素对的联合概率。Graycoprops使用正规化的GLCM来计算属性。
      属性参数如下：
      1.  ‘Contrast‘ : 对比度。返回整幅图像中像素和它相邻像素之间的亮度反差。取值范围：[0,（GLCM行数-1）^2]。灰度一致的图像，对比度为0。
      2.  ‘Correlation‘ : 相关。返回整幅图像中像素与其相邻像素是如何相关的度量值。取值范围：[-1,1]。灰度一致的图像，相关性为NaN。
      3.  ‘Energy‘ : 能量。返回GLCM中元素的平方和。取值范围：[0 1]。灰度一致的图像能量为1。
      4.  ‘Homogemeity‘ : 同质性。返回度量GLCM中元素的分布到对角线紧密程度。取值范围：[0 1]。对角矩阵的同质性为1。

........代码有专门的距离参数，设置我们取像素点应该是取相邻的还是啥.....................................................

技术分享

.......................................................................................................
示例：

计算灰度共生矩阵，并且返回缩放后的图像，SI
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,‘NumLevels‘,9,‘G‘,[])

计算灰度图像的灰度共生矩阵
I = imread(‘circuit.tif‘);
glcm = graycomatrix(I,‘Offset‘,[2 0]);

灰度共生矩阵的特征：

角二阶矩（Angular Second Moment, ASM)
ASM=sum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵
角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量，当图像纹理绞细致、灰度分布均匀时，能量值较大，反之，较小。

熵（Entropy, ENT)
ENT=sum(p(i,j)*(-ln(p(i,j)))
是描述图像具有的信息量的度量，表明图像的复杂程序，当复杂程序高时，熵值较大，反之则较小。

反差分矩阵（Inverse Differential Moment, IDM)
IDM=sum(p(i,j)/(1+(i-j)^2))
反映了纹理的清晰程度和规则程度，纹理清晰、规律性较强、易于描述的，值较大；杂乱无章的，难于描述的，值较小。