标签:


1 #include <cstdio> 2 #include <algorithm> 3 #define MAXN 100005 4 using namespace std; 5 6 int a[MAXN],b[MAXN],n,tot,root[MAXN],q,l,r,k,link[MAXN],t; 7 8 struct Node 9 { 10 int ls,rs,size; 11 }; 12 Node tree[MAXN*20]; 13 14 struct cmp 15 { 16 bool operator () (int i,int j) 17 { 18 return (a[i]《a[j]); 19 } 20 }; 21 cmp x; 22 23 void discretize() 24 { 25 sort(link+1,link+n+1,x); // 以link作为中转站,对a进行排序 26 for (int i=1;i<=n;i++) b[link[i]]=i; 27 } 28 29 void insert(int &now,int l,int r,int x) 30 { 31 tree[++tot]=tree[now]; now=tot; 32 tree[now].size++; 33 if (l==r) return; 34 int mid=(l+r)>>1; 35 if (x<=mid) insert(tree[now].ls,l,mid,x); 36 else insert(tree[now].rs,mid+1,r,x); 37 } 38 39 int query(int nl,int nr,int l,int r,int k) 40 { 41 if (l==r) return l; 42 int size=tree[tree[nr].ls].size-tree[tree[nl].ls].size,mid=(l+r)>>1; 43 if (size>=k) return query(tree[nl].ls,tree[nr].ls,l,mid,k); 44 else return query(tree[nl].rs,tree[nr].rs,mid+1,r,k-size); 45 } 46 47 int main() 48 { 49 freopen("HDU2665.in","r",stdin); 50 freopen("HDU2665.out","w",stdout); 51 scanf("%d",&t); 52 for (int j=1;j<=t;j++) 53 { 54 root[0]=0; tot=0; 55 scanf("%d %d",&n,&q); 56 for (int i=1;i<=n;i++) { scanf("%d",&a[i]); link[i]=i; } 57 discretize(); // 离散化 58 for (int i=1;i<=n;i++) 59 { 60 root[i]=root[i-1]; 61 insert(root[i],1,n,b[i]); 62 } 63 for (int i=1;i<=q;i++) 64 { 65 scanf("%d %d %d",&l,&r,&k); 66 printf("%d\n",a[link[query(root[l-1],root[r],1,n,k)]]); 67 } 68 } 69 return 0; 70 }
++++++++++++++++++++++++++++我是华丽丽的分割线++++++++++++++++++++++++++++
【总结】
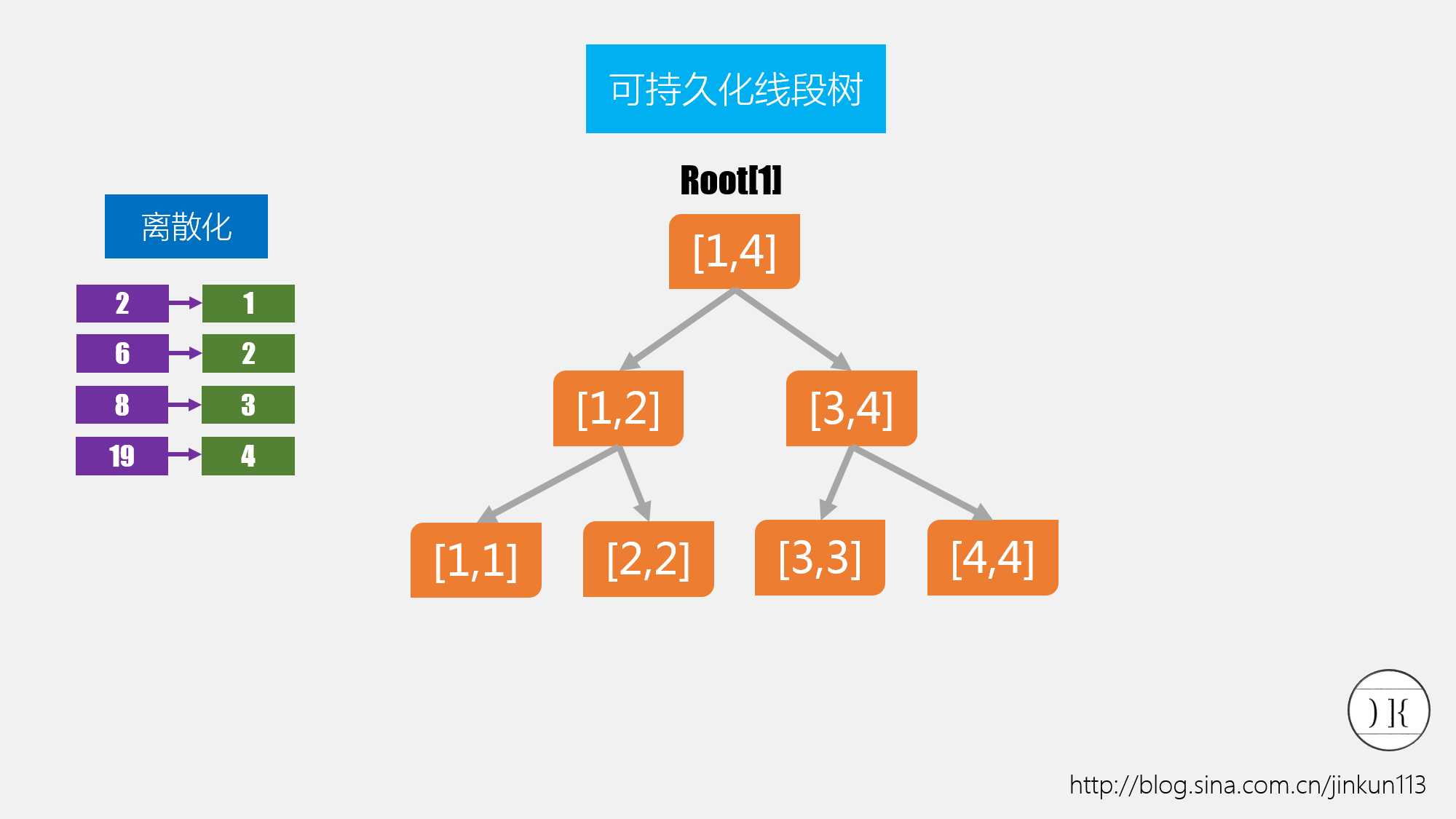
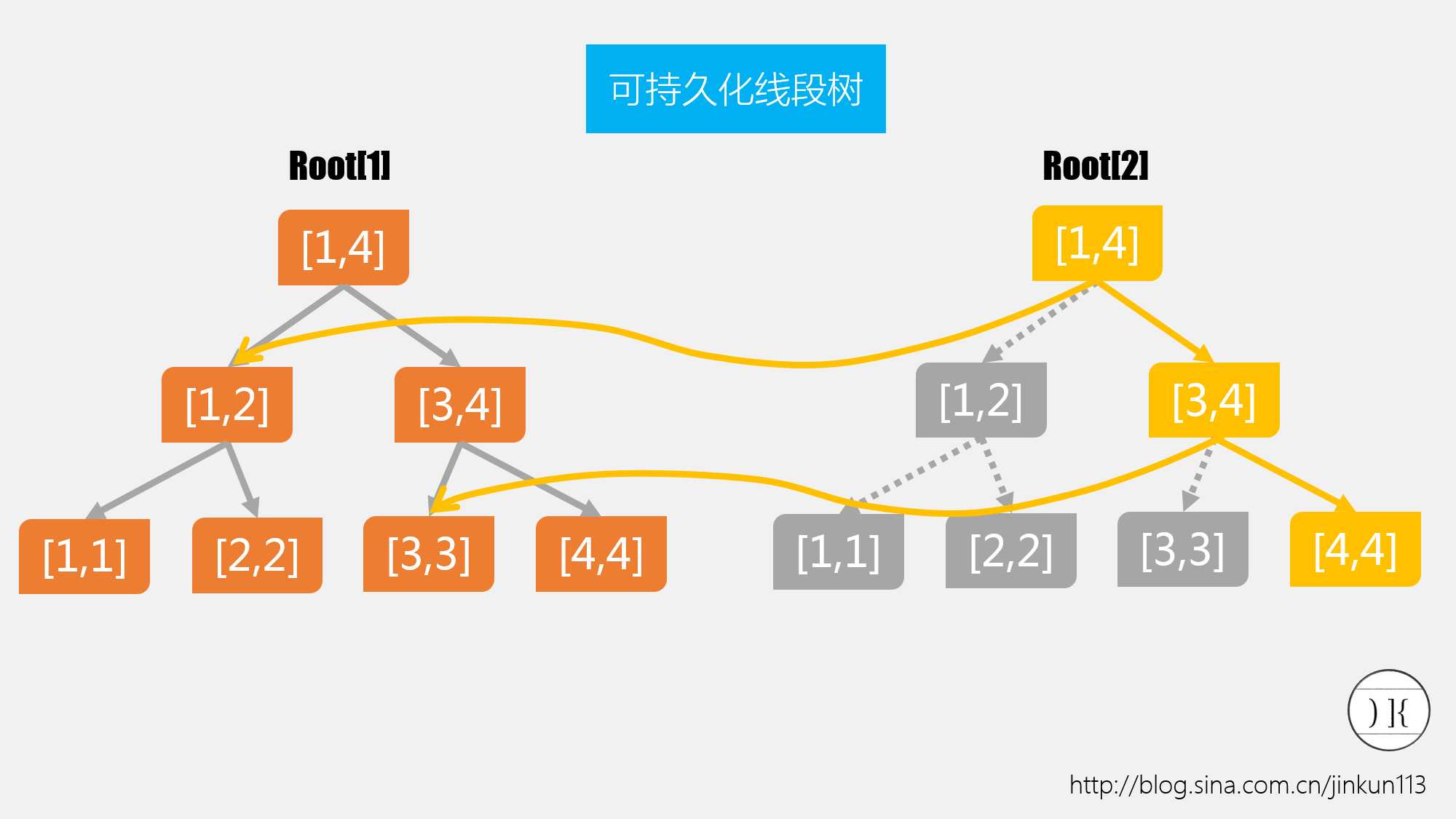
单纯的可持久化线段树主要适用于一类只包含查询而不包含修改的(广义)区间查询问题,这类问题至少满足下面的 第二项条件:1、整体查询可利用(离散化后的)权值线段树解决,部分区间却无法解决;2、每一个元素的状态可表示为某个前趋元素的修改版本,修改通常是极 少的——具体来说,在线段树中只会修改常数条链。
如果条件1、2都具备,我们通常可以建立具有前缀和性质的可持久化线段树解决。所谓前缀和性质,指的是对每个元素i建立线段树T(i)后,T(i)包含了1-i的信息,而这个信息是可减的。我 们可以利用树的减法将部分区间变为整个区间。具体来说,对于线性表上的查询[l,r],常用的模式是Query(T(l)-T(r-1));对于树上路径 的查询,由于每个节点都有惟一的前趋节点,我们可以把路径视作一种广义的区间,查询[l,r]时,设p=lca(l,r),常用的查询模式是 Query(T(l)+T(r)-T(p)-T(par[p]))(对点)或Query(T(l)+T(r)-2T(p))(对边)。
如果只具备条件2,我们常常不利用前缀和性质(也常常无法利用),而是将区间问题转化为点问题,单独查询某个点上的线段树,并在特定的一棵线段树上获取区间信息。这时,可能需要二分答案。这一类问题的典型例子是BZOJ2653。
上述一类问题的解决过程中,在建树时通常需要利用上一节点的已有版本。
如果题目还要求修改操作,单纯的可持久化线段树通常不能完成。这时,对于满足上述1、2条件的问题,我们会发 现,修改一个版本的线段树会对后续版本造成影响——这与修改前缀和数组中某个值会对后继值造成影响是类似的。因此,我们可以考虑使用树状数组维护前缀和。 如果是树上的问题,我们可以建立DFS序的树状数组来维护前缀和。这样,节点不存在明确的前趋,建树时也就不再需要利用上一节点的已有版本了。
只满足上述条件2且需要修改的题目我还在思考中,不知道有没有这一类的题目(如带修改的bzoj2653)。此外,我还在考虑可持久化线段树更复杂的应用(如区间运算?),因此这个总结未来也许会更新。
标签:
原文地址:http://www.cnblogs.com/SBSOI/p/5649373.html