标签：
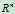:包含所有n维的列向量（之所以使用R：列向量的元素都是实数）
在所有向量空间内都支持的操作：
实数向量空间：
8个规则：
用的较多的还是向量空间和子空间的定义，即乘法和加法的结果仍在集合内。子空间也是向量空间
相反的方面，若一个集合不能构成向量空间，则这个集合的元素相加或相乘的结果可能不在这个集合内。
子空间：
零向量是任何向量空间的子空间。
最小的子空间仅由一个向量构成：0向量。称作0维空间。向量空间不允许是空集。
最大的子空间就是原始的向量空间本身。
3维空间的子空间：
子空间可以缩小维度（由上图），但实质都是从原始空间点集抽出的一个子集和，集合中的元素都来自原始集合。
列向量空间：
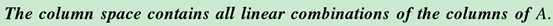
注意向量空间的原子是‘列‘（概念上的列，列实际可以是各种形式，如一个函数，一个矩阵）。
方程解与列向量空间的联系：
对于
Ax = b can be solved if and only if b lies in the plane that is spanned（标定） by the two column vectors .这个plane就是
的列向量空间，同时也是
的子空间（过0点）。这个plane是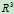
的子空间的证明 p89
C（A）：A的列向量空间，是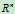
的子空间，证明p89。注意
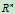是我们讨论各种问题所在的全集，就类似与1属于自然数n这种关系。
N（A）：A的nullspace，是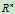
的子空间,证明：
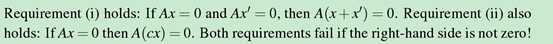
x+x‘在nullspace内，cx也在nullspace内，所以x的全集是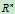
的子空间
注意一开始用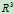
举线性组合的例子，A里只有两列(这种情况就高斯消元法来讲一定是奇异的情况，pivots个数不够！)，这时候列向量空间是个面，A中也可以有三列的-----
Nullspace:
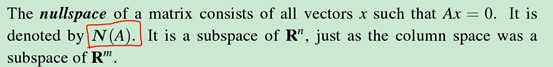
注意：之前说的向量空间都是由b直接构成，nullspace似乎不是这样，它是由构成0向量空间的线性组合的系数构成的，有点区别，还有如果A的列数小于行数的话似乎看b更直观一些。
独立，或者说成线性无关。
了解C(A)和N(A)的目的：
问题集合：
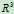的子空间由四种类型：
本身，面，线，零。
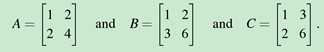
[??]B的列向量空间已经和A的不同了，列向量空间和解是什么关系呢？C的列向量空间仍和A一致。
4.a能由两个向量唯一确定，但是不能由三个向量唯一确定
.
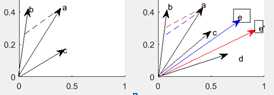
c和d可以确定任意多个向量如e和e‘,e在和b确定a.
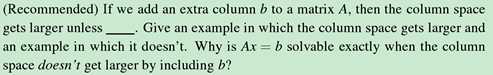
除非b在A的向量空间内，由上面第二图可知，添加了一个仍在A的向量空间内的d仍是可解的。
标签：
原文地址：http://www.cnblogs.com/wangxiaotao/p/5650665.html
