标签:
分类变量、连续变量分布的描述
bootstrap抽样、秩和检验探索变量关联:比较均值、独立样本
变量变换:P-P图
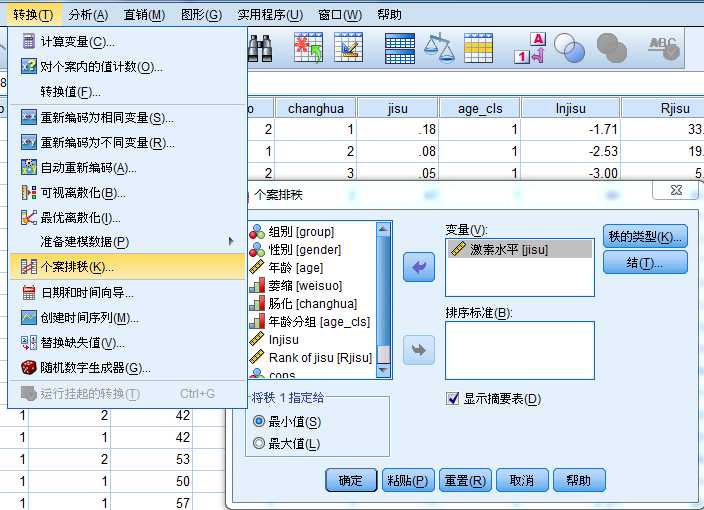
秩变换分析:个案排秩
Cox回归模型
方差分析实质是自变量含有分类变量的一般线性模型。
方差分析属于参数检验,有一定的假设条件。当不满足方差分析的假设条件时,就选择
(1)非参数检验(bootstrap抽样、秩和检验)方法-实际上是一种初判的方法;
(2)或考虑变量变换,对变换后的变量进行方差分析;-应用广泛
(3)或变量变换无法解决时,考虑秩变换分析方法。即对原变量的秩次进行方差分析;-应用更广
(4)秩变换分析方法会损失一些数据信息,考虑用生存分析中的Cox回归模型分析。
对于本章案例,三种方法的分析结果一致,不同组的激素水平差异显著,性别、年龄对激素水平无影响。
1、案例背景
在控制其他因素的作用下,研究激素水平是否在对照组和试验组(患有胃癌)两个组间存在差异。
2、数据理解
单变量描述:
看分类变量的频数分布,常用的方法是描述过程、频率过程或制表过程。下面是用制表过程来简化输出分类变量的频率分布。
看连续变量的分布在描述过程,通过画直方图看连续变量是否是正态分布。
结论:激素水平是呈明显的右偏态分布。下面要考虑激素水平的分布是否满足模型对数据分布的要求,若不满足,则如何处理。
变量关联探索:
目标:非参数检验就是在不假定参数服从正态分布的前提下,识别不同组间差异的显著性。
上面分析了单变量的分布情况,那要想看下如:激素水平在不同组、性别、年龄段的分布情况,需要进行变量关联探索,比较不同因素下的激素水平均值大小。
由于激素水平是偏态分布,所以用bootstrap抽样、秩和检验进行组别间的均值比较。
下面是bootstrap抽样:
bootstrap抽样有参数法和非参数法。参数法是先假定参数的分布状况,非参数法是不假定分布。
当频数分布近似正态时,用均值做点估计,用正态原理估计bootstrap可信区间;当频数分布为偏态分布时,用中位数做点估计,用上下2.5%分位数估计95%置信区间。
此处用中位数表示各组平均水平,计算中位数的置信区间来大致估计不同因素下的激素水平有无统计差异。
“分析-比较均值-均值”
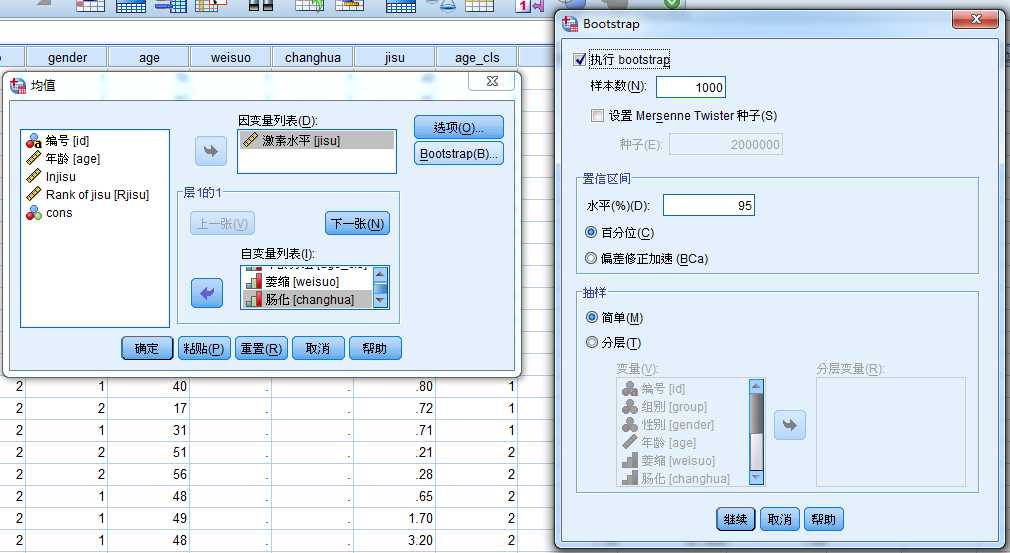
初步结论:激素水平的中位数在两个组别间存在差异。
下面是秩和检验:
给出更精确的组间是否存在差异的结果。
SPSS提供新老两套秩和检验的操作界面,分别如下:
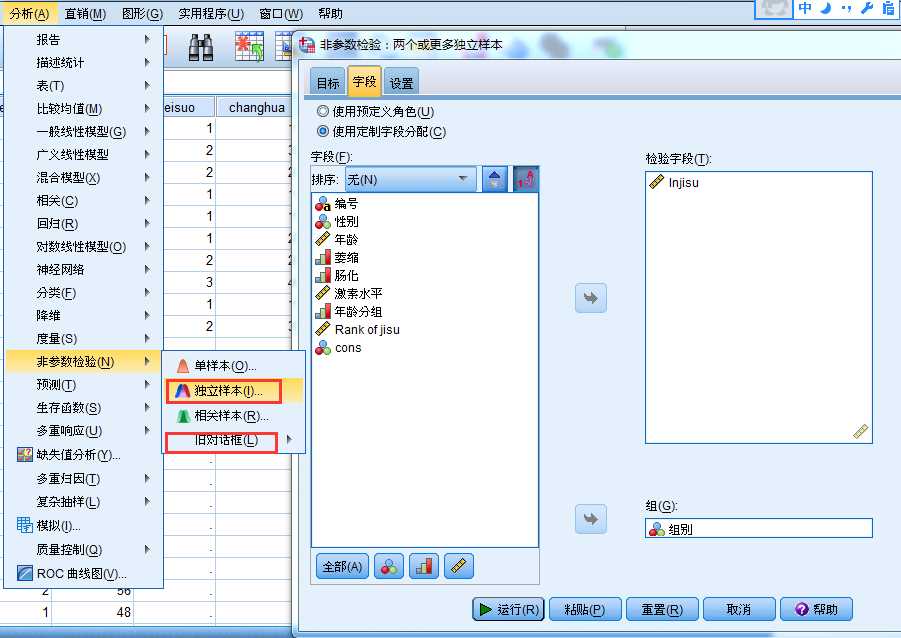
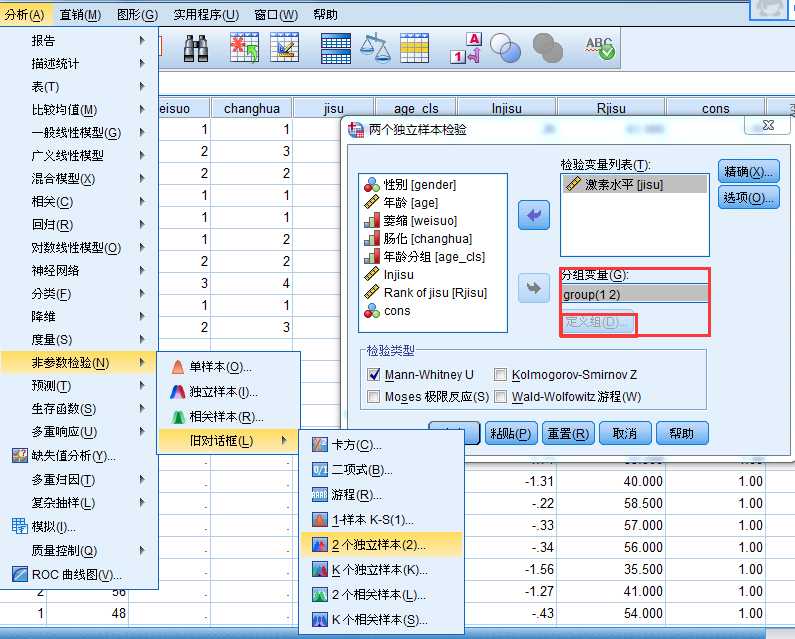
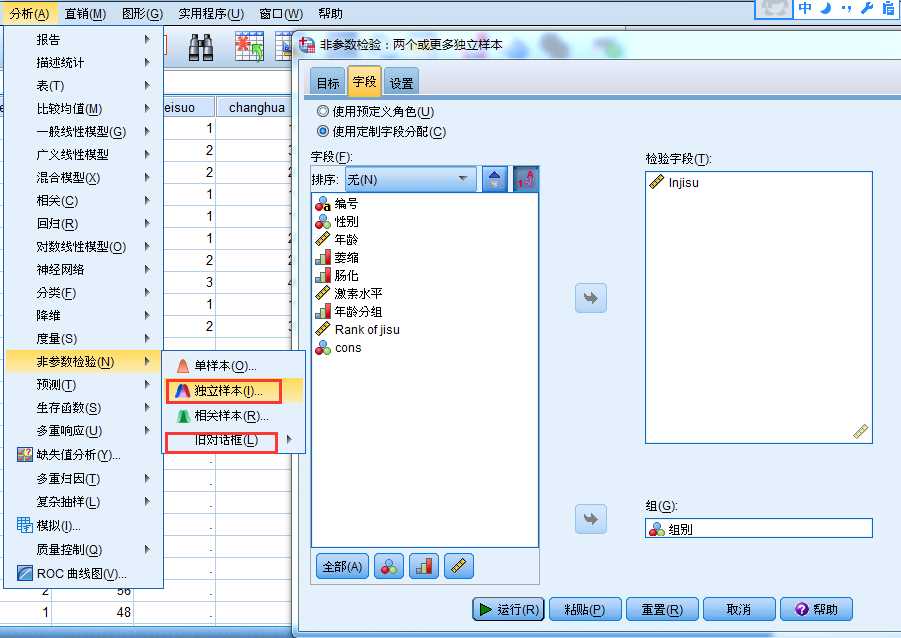
用散点图探讨年龄与激素水平的关系:
对于探索两个连续变量的联系,绘制散点图是第一选择。
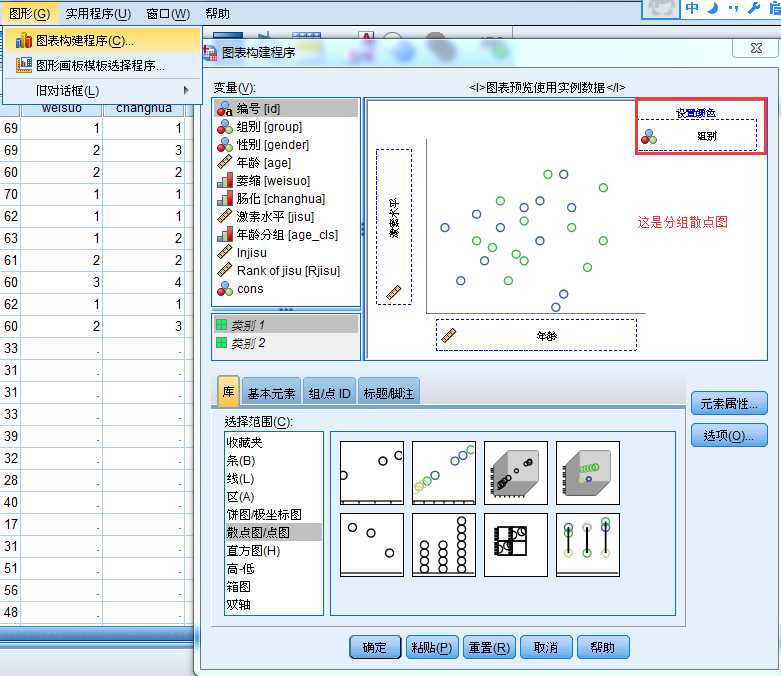
3、对因变量变换后的建模分析
常见的变量变换方法:
对数变转换、平方根转换、倒数转换等等。
本案例的具体操作:
对因变量激素水平进行对数变换,看是否满足方差分析的要求。
变量变换,即通过对原始数据的数学变换,使其成为满足或近似满足方差分析的要求,对变换后的变量进行方差分析。
检验对数变换后的激素水平是否进行满足正态分布:P-P图
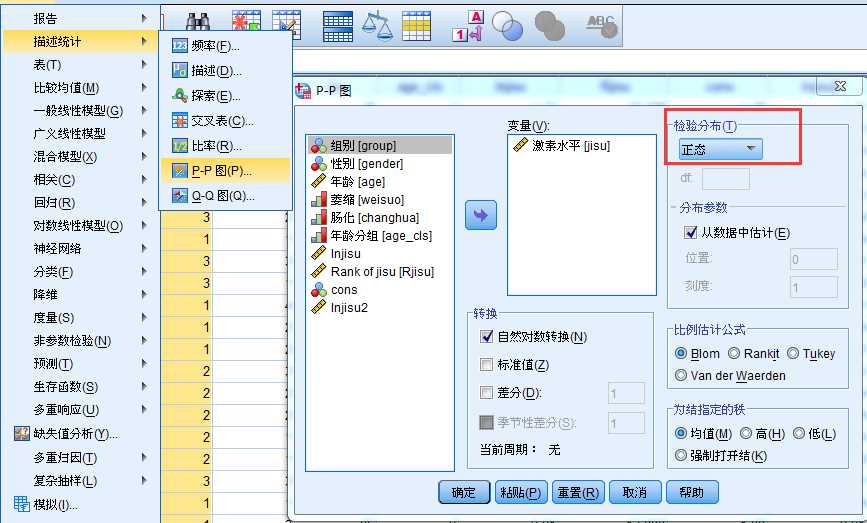
结果显示:对数变换后的激素水平已较为接近正态,可建立方差分析模型。
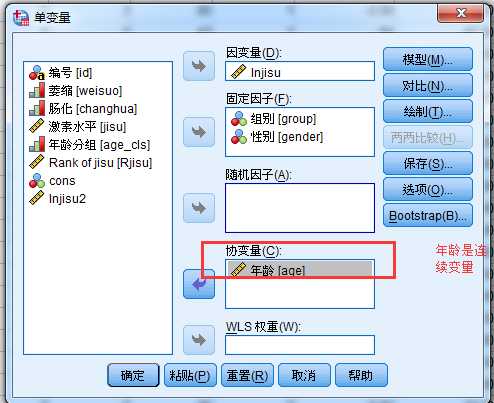
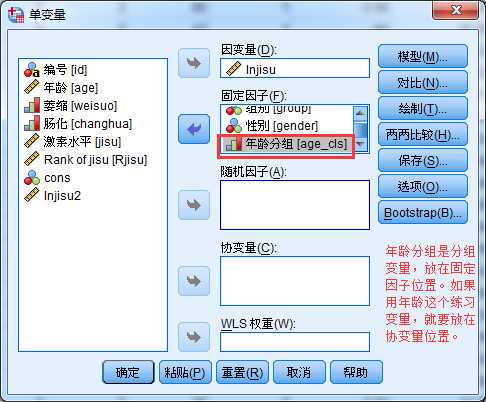
“缺乏拟合优度检验”是检验已建模型与饱和模型(即包括所有主效应和交互效应的模型)相比,当前模型的预测效果是否存在差异。
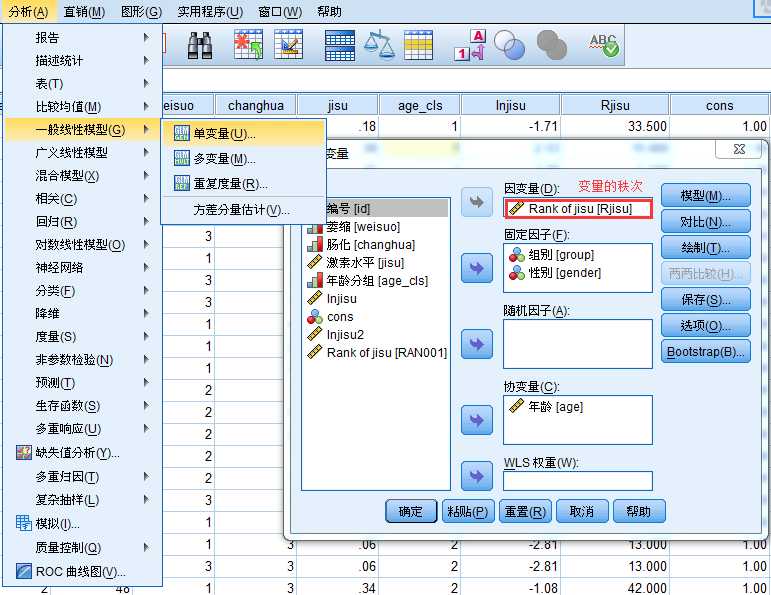
4、秩变换分析
当变量变换无法解决问题时,考虑使用非参数统计分析方法中的秩变换分析方法。
所谓秩变换分析方法就是先求出原变量的秩次,然后使用求出的秩次代替原变量进行参数分析。即对求出的秩次进行方差分析。
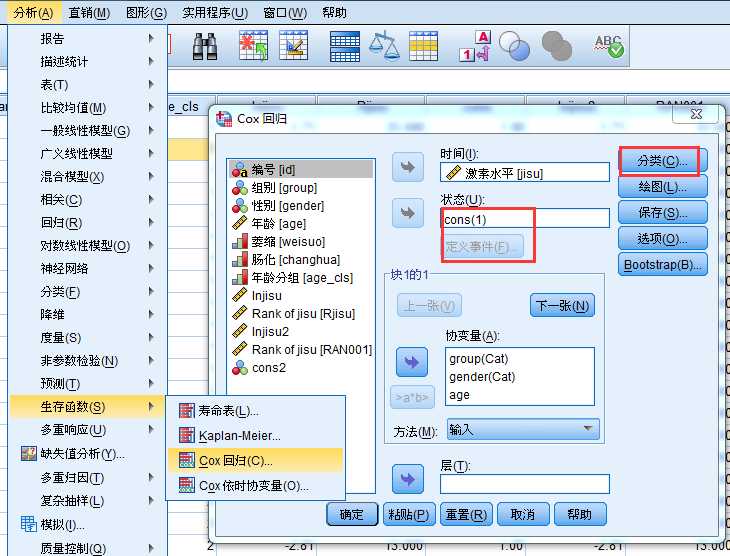
5、利用Cox模型进行分析
秩变换分析方法通过利用秩次的方式来绕开数据非正态分布的问题,但会丢失一些信息。解决办法是使用生存分析中的Cox回归模型分析。
事件:由研究者规定的生存时间的终点。
Cox回归模型的基本思想:在风险函数与研究因子之间建立类似于广义线性模型的关联。
激素水平:理解为生存时间;
由于每个样本都有明确的激素水平测量值,即生存时间,则每个人的生存结局都是出现了失效事件。失效事件数值=1.
ch7-偏态分布的激素水平影响因素分析-深入学习方差分析模型
标签:
原文地址:http://www.cnblogs.com/yaofang/p/5651129.html