标签:
一、线性规划问题
已知目标函数和约束条件均为线性函数,求目标函数的最小值(最优值)问题。
1.求解方式:用linprog函数求解
2.linprog函数使用形式:
x=linprog(f,A,b)
x=linprog(f,A,b,Aeq,beq)
x=linprog(f,A,b,Aeq,beq,lb,ub)
x=linprog(f,A,b,Aeq,beq,lb,ub,x0)
x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval]=linprog(…)
[x, fval, exitflag]=linprog(…)
[x, fval, exitflag, output]=linprog(…)
[x, fval, exitflag, output, lambda]=linprog(…)
3.介绍一种最常用的:
[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aep,beq,lb,ub);
其中,f是目标函数系数矩阵;A和b是不等式约束条件的参数;Aeq和beq是等式约束条件的参数;lb和ub为x取值的取值范围。
lambda.ineqlin—不等式约束A,b
lambda.eqlin—等式约束Aep,bep
lambda.upper—上界条件ub
lambda.lower—下界条件lb
4.实例:
目标函数:f(x) = –5x1 – 4x2 –6x3,
约束条件:
x1 – x2 + x3 ≤ 20
3x1 + 2x2 + 4x3 ≤ 42
3x1 + 2x2 ≤ 30
0 ≤ x1, 0 ≤ x2, 0 ≤ x3
Matlab程序:
>> f = [-5; -4; -6]; A = [1 -1 1; 3 2 4; 3 2 0]; b = [20; 42; 30]; lb = zeros(3,1); >> [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb); >> x x = 0.0000 15.0000 3.0000 >> fval fval = -78.0000
二、二次型规划问题
理解完线性规划问题再来学习二次型规划问题就简单得多了,可以相似类比。
1.求解方式:用quadprog函数来求解
2.quadprog函数使用形式:
x = quadprog(H,f)
x = quadprog(H,f,A,b)
x = quadprog(H,f,A,b,Aeq,beq)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
x = quadprog(problem)
[x,fval] = quadprog(H,f,...)
[x,fval,exitflag] = quadprog(H,f,...)
[x,fval,exitflag,output] = quadprog(H,f,...)
[x,fval,exitflag,output,lambda] = quadprog(H,f,...)
3.实例:
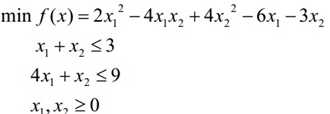
Matlab程序:
>> H = [4 -4;-4 8];f = [-6;-3];A = [1 1;4 1];b = [3;9];lb = ones(2,1); >> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb); >> x x = 1.9500 1.0500 >> fval fval = -11.0250
注:若求解的是最大值问题亦可转化为求最优化问题。
标签:
原文地址:http://www.cnblogs.com/always-chang/p/5652867.html