标签:
这一章节我们开始对多重积分的研究。
在此之前,我们首先来回忆起积分的过程,在平面中,面临求解不规则图形的面积(常叫曲边梯形)的时候,我们可以采取建立直角坐标系,然后通过得到不规则图形边界的函数表达式f(x),对f(x)求解一次定积分即可。其方法就是先微分(将自变量区间划分为n个区间段),引入极限的概念(即使得n趋向无穷)之后使得我们能够“化曲为直”,然后利用矩形的面积公式进行求解。随后是积分过程,将这n个小矩形相加求极限,可得曲边梯形的面积。
如下几图使得这个过程更加的直观.
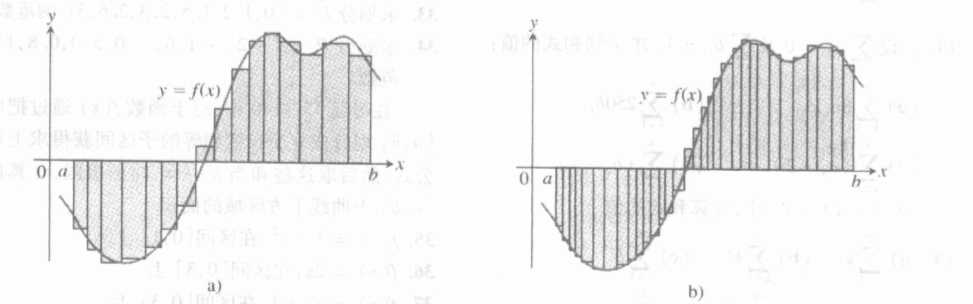
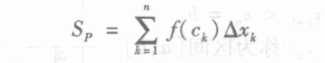
Sp又叫做,f(x)在[a,b]上的黎曼和。
关于黎曼和,这里简单的插一句,关于积分的定义在牛顿时代就已经给出了,但是它现代数学的的定义是后来黎曼给出的。关于黎曼和,存在着很多形式。
由于积分和微分是逆运算,由此根据导数的定义可给出积分符号∫。
那么我们把一开始求曲边梯形的面积推广到空间,对于带曲面的不规则几何体,我们如何求解其体积呢?
像这个图一样。(其顶部是一个曲面,底面在x-O-y面上)
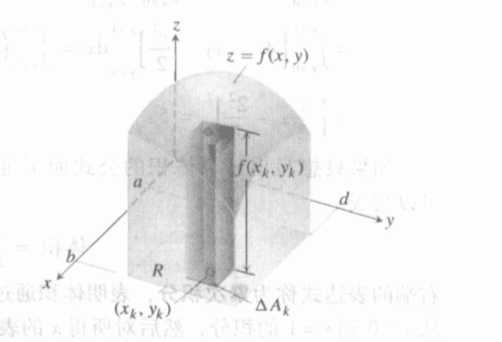
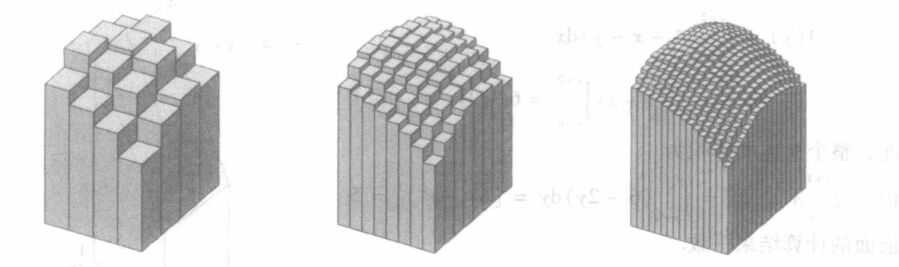
类比处理曲边梯形面积的思想,这里我们建立三维坐标系,用二元函数z = f(x,y)来表征最上面的曲面,我们从它的底面分析,考虑“化曲为直”将其往长方体上靠拢。
我们将底面的矩形用一些平行于x、y的直线,将其划分成n个小矩形,并标号。记第i个矩形的长为△xi,宽为△yi,第i个小矩形的面积是△Ai=△xi△yi。
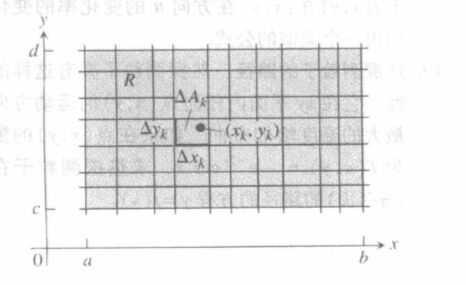
容易看到,我们可以近似的将不规则几何体看成由n个长方体组成,那么会得到如下的黎曼和的形式:
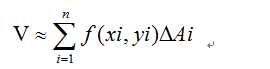
而很容易看到,随着n趋于无穷,约等式右边的和式将无限的接近V。
如下图所示。
因此我们得到:
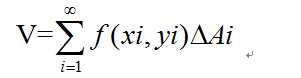
可以看到,这里我们有两个维度的微小圆,因此我们要在两个维度上进行积分,因此我们采用如下的表述方式:
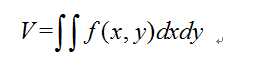
《University Calculus》-chaper13-多重积分-二重积分的引入
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5654026.html