标签:
红黑树是一棵二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是Red或Black。
通过对任何一条从根到叶子节点简单路径上的颜色来约束树的高度,红黑树保证最长路径不超过最短路径的两倍,因而近似于平衡。
红黑树是满足下面红黑性质的二叉搜索树:
1. 每个节点,不是红色就是黑色的
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个子节点是黑色的(不存在连续的红色节点)
4. 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
思考:为什么满足上面的颜色约束性质,红黑树能保证最长路径不超过最短路径的两倍?
最短的路径上节点的颜色全部都为黑色;最长的路径则为黑红交叉的路径,其上有与最短路径的黑节点数目相同的黑节点数和红节点数目。所以我们按照红黑树性质所建立的红黑树的最长路径必然不会超过最短路径的两倍!
建立红黑树的节点类:
插入的新节点默认是红色的。原因是:插入黑节点必然会影响所有路径都含有相同数目的黑色节点这一原则,较难维护!
enum Color
{
RED,
BLACK
};
template<class K,class V>
struct RBTreeNode
{
K _key;
V _value;
Color _color; //颜色
RBTreeNode<K, V>* _left; //指向左孩子的指针
RBTreeNode<K, V>* _right; //指向右孩子的指针
RBTreeNode<K, V>* _parent; //指向父节点的指针
RBTreeNode(const K& key=K(), const V&value=V())
:_key(key)
, _value(value)
, _color(RED)
, _left(NULL)
, _right(NULL)
, _parent(NULL)
{}
};
红黑树需要变色或利用旋转来降低高度的几种情况:
图注:g代表grandfather祖父节点;p代表parent父亲结点;u代表uncle叔叔节点;cur代表当前节点
一、父节点是祖父节点的左孩子
1.uncle的颜色是红色
①当前节点cur是parent的左孩子
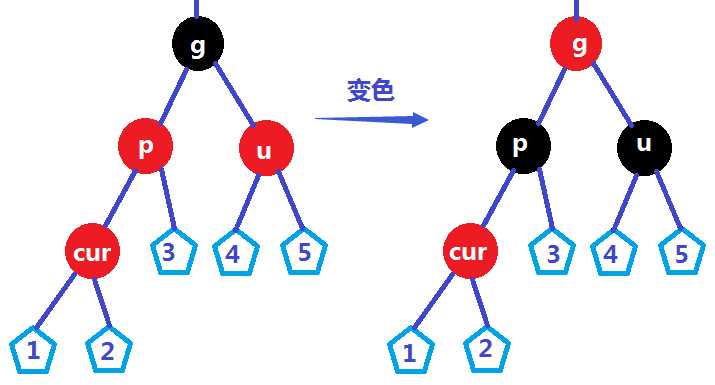
②当前节点cur是parent的右孩子
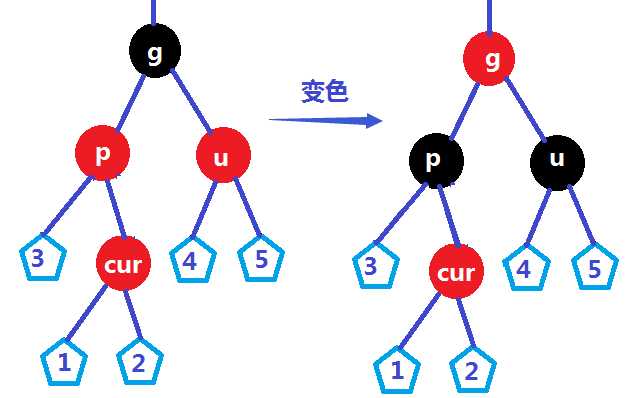
2.uncle的颜色是黑色 或者 uncle为NULL
①cur是parent的左孩子,右单旋
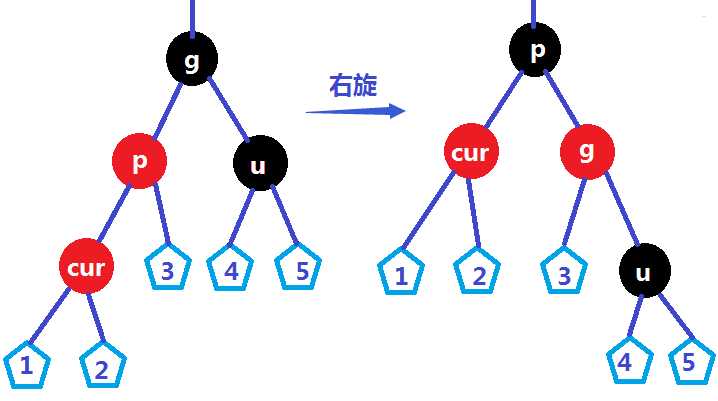
②cur是parent的右孩子,先左后右双旋
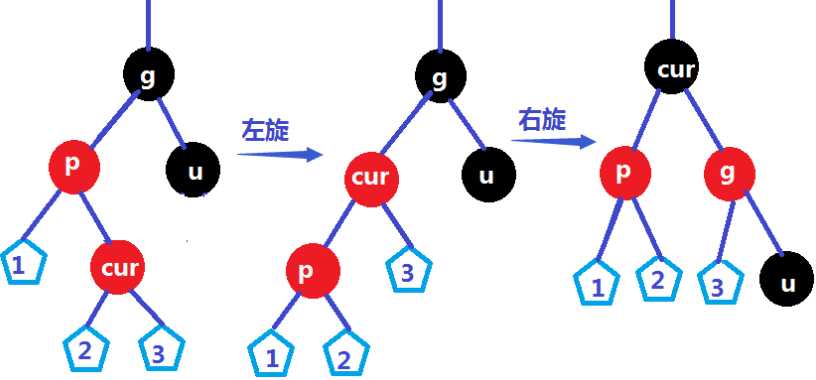
二、父节点是祖父节点的右孩子
1.uncle的颜色是红色
①cur是parent的右孩子
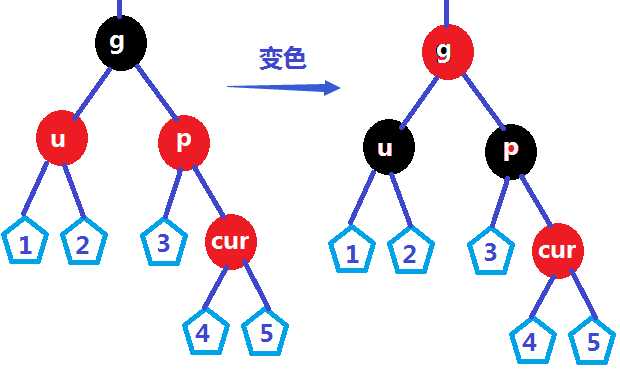
②cur是parent的左孩子
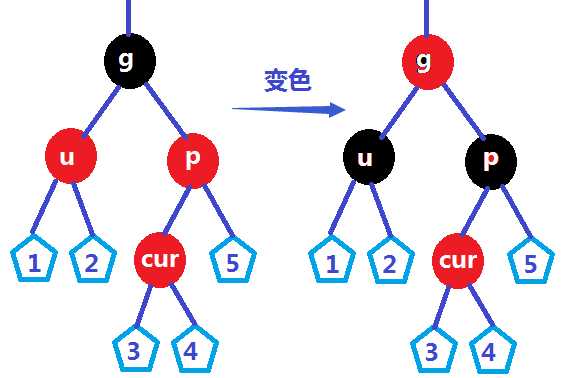
2.uncle的颜色是黑色 或者 uncle为NULL
①cur是parent的右孩子
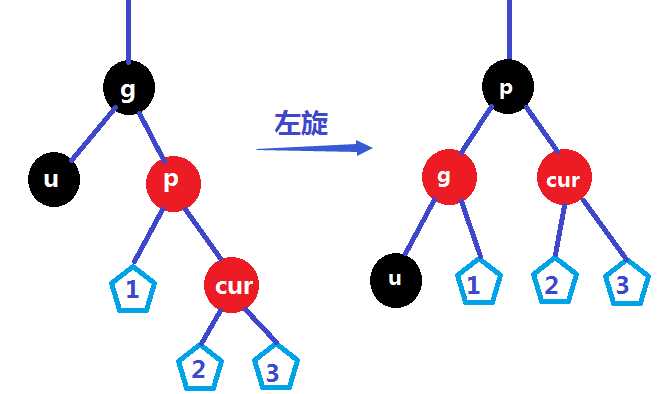
②cur是parent的左孩子
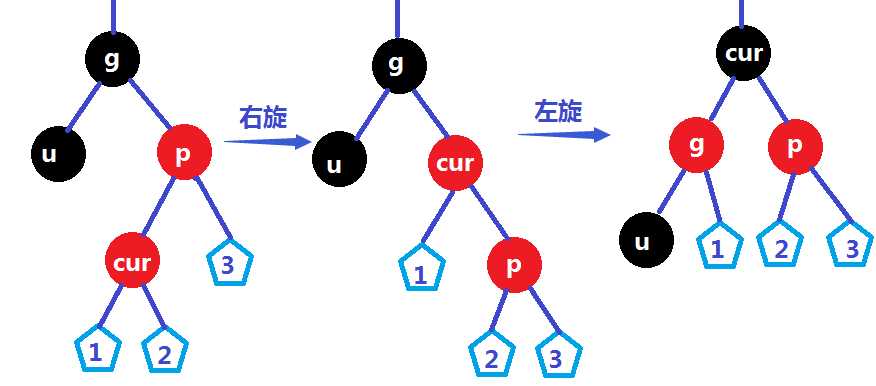
插入节点:
基于以上的情况,红黑树利用模板类封装的插入函数算法就完成了:
template<class K, class V>
bool RBTree<K, V>::Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new RBTreeNode<K, V>(key, value);
_root->_color = BLACK;
return true;
}
// 找位置
RBTreeNode<K, V>* cur = _root;
RBTreeNode<K, V>* parent = NULL;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
//插入
cur = new RBTreeNode<K, V>(key, value);
cur->_parent = parent;
if (parent->_key > key)
parent->_left = cur;
else if (parent->_key < key)
parent->_right = cur;
//检查颜色分配是否满足要求
while (parent&&parent->_color==RED)
{
RBTreeNode<K, V>* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
RBTreeNode<K, V>* uncle = grandfather->_right;
if (uncle&&uncle->_color == RED)
{ //第一种情况 变色
grandfather->_color = RED;
parent->_color =BLACK;
uncle->_color = BLACK;
cur = grandfather;
parent = grandfather->_parent;
}
else if( (uncle&&uncle->_color==BLACK)||uncle==NULL)
{
if (cur == parent->_left)
{//第二种情况 右单旋 cur必然有黑色孩子
parent->_color = BLACK;
grandfather->_color = RED;
RotateR(grandfather);
}
else
{//第三种情况 左右双旋
RotateL(parent);
parent->_color = BLACK;
grandfather->_color = RED;
RotateR(grandfather);
}
break;
}
}
else if (parent == grandfather->_right)
{
RBTreeNode<K, V>* uncle = grandfather->_left;
if (uncle&&uncle->_color == RED)
{//第一种情况 变色
grandfather->_color = RED;
parent->_color = BLACK;
uncle->_color = BLACK;
cur = grandfather;
parent = cur->_parent;
}
else if( (uncle&&uncle->_color == BLACK)||uncle==NULL)
{//第二种情况 左单旋 cur必然有黑孩子
if (cur == parent->_right)
{
parent->_color = BLACK;
grandfather->_color = RED;
RotateL(grandfather);
}
else if (cur==parent->_left)
{//第三种情况 右左双旋
RotateR(parent);
parent->_color = BLACK;
grandfather->_color = RED;
RotateL(grandfather);
}
break;
}
}
}
_root->_color = BLACK;
return true;
}
插入完成之后,我们无法直观的看出红黑树的节点颜色是否合法,也无法直观的看出每条路径的黑色节点数目是否相同。
所以,这里实现两个函数,方便检验红黑树的合法性。
//检验红黑树的合法性
template<class K, class V>
bool RBTree<K, V>::Check()
{
//统计红黑树每条路径上黑色节点的数量
int blackNum = 0;
RBTreeNode<K, V>* cur = _root;
while (cur)
{
if (cur->_color == BLACK)
blackNum++;
cur = cur->_left;
}
int CBNum = 0;
return _Check(_root,blackNum,CBNum);
}
////////////////// 递归辅助
template<class K, class V>
bool RBTree<K, V>::_Check(RBTreeNode<K, V>* root, int blackNum, int CBNum)
{
if (root == NULL)
return true;
if (root->_color == BLACK)
{
CBNum++;
if (root->_left == NULL&&root->_right == NULL)
{ //走到了叶子节点 将该条路径上的黑色节点数量与之前统计的黑色节点数量做比较
if (blackNum == CBNum)
{
return true;
}
else
{
cout << "叶子节点为" << root->_key << "路径的黑色节点数目与最左侧支路的黑色节点数目不相等 !" << endl;
return false;
}
}
}
else if (root->_parent&&root->_parent->_color == RED)
{//判断是否存在连续的两个红色节点
cout << root->_parent->_key << " 和 " << root->_key << " 为两个连续的红色节点" << endl;
return false;
}
//递归检验子路
return _Check(root->_left, blackNum, CBNum) && _Check(root->_right, blackNum, CBNum);
}
红黑树和AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删查改的时间复杂度都是O(lg(N)) 红黑树的不追求完全平衡,保证最长路径不超过最短路径的2倍,相对而言,降低了旋转的要求,所以性能会优于AVL树,所以实际运用 中红黑树更多。
标签:
原文地址:http://www.cnblogs.com/Lynn-Zhang/p/5653943.html