标签:
在市场研究中,有一种分析是研究消费者态度或偏好,收集的数据是某些对象的评分数据,这些评分数据可以看做是对象间相似性或差异性的表现,也就是一种距离,距离近的差异性小,距离远的差异性大。而我们的分析目的也是想查看这些对象间的差异性或相似性情况,此时由于数据的组成形式不一样,因此不能使用对应分析,而需要使用一种专门分析此问题的方法——多维尺度分析(MDS模型)。多维尺度分析和对应分析类似,也是通过可视化的图形阐述结果,并且也是一种描述性、探索性数据分析方法。
基于以上,我们可以得知,多维尺度分析经常使用在市场研究中:
① 可以确定空间的维数(变量、指标),以反映消费者对不同品牌的认知,并且在由这些维构筑的空间中,标明某关注品牌和消费者心目中理想品牌的位置,选择的品牌不宜过少也不宜过多,一般7-9个。
② 可以比较消费者和非消费者对企业形象的感觉。
③ 在进行市场细分时,可以在同一空间对品牌和消费者定位,然后把具有相似感觉的消费者分组、归类。
④ 在新产品开发方面,通过在空间图上寻找间隙,可以发现由这些间隙为企业带来的潜在契机。
⑤ 在广告效果的评估方面,可以用空间图去判定一个广告是否成功地实现了期望的品牌定位。
⑥ 在价格策略方面,通过比较加入与不加入价格轴的空间图,可以推断价格的影响强度。
⑦ 在分销渠道策略方面,利用空间图可以判断品牌对不同零售渠道的适应性,从而为制定有效的分销渠道提供依据。
在市场研究中,我们要注意的是选择的品牌数量要适中,并且分析的问题要明确,每组数据只能分析一个问题,比如对一组饮料产品收集的数据不能既反映口感又反映价格。
多维尺度分析收集的数据值大小必须能够反应两个研究对象的相似性或差异性程度。这种数据叫做邻近数据,所有研究对象的邻近数据可以用一个邻近矩阵表示。反映邻近的测量方式有:
相似性-数值越大对应着研究对象越相似。 差异性-数值越大对应着研究对象越不相似。
测量邻近性数据的类型有:
①两个地点(位置)之间的实际距离。(测量差异性)
②两个产品之间相似性或差异性的消费者心理测量。(差异性或相似性)
③两个变量的相关性测量。(相关系数测量相似性)
④从一个对象过渡到另一个对象的转换概率。例如概率反应了消费者对品牌或产品偏好的变化。(测量相似性)
⑤反映两种事物在一起的程度。例如:用早餐时人们经常将哪两种食品搭配在一起。(测量相似性)
⑥谁喜欢谁,谁是谁的领导,谁传递给谁信息,谁是谁的上游或下游等等社会网络数据等(测量相似性)
邻近数据即可以直接测量(距离),也可以通过计算得到(变量间的相关系数)。
多维尺度模型根据测量的尺度不同可以分为:
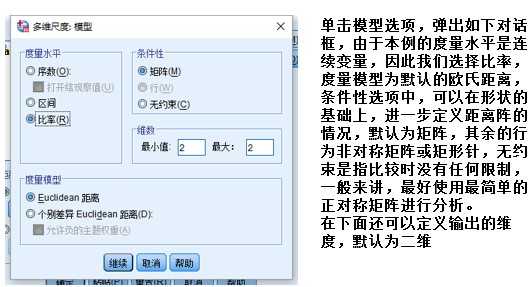
①古典MDS模型,针对收集的数据为比率和区间,也就是直接可以测量距离的情况
②非度量MDS模型,收集的数据为有序数据,针对无法直接测量距离,只能通过评分测量的情况
根据测量的个体数量不同,可以分为
①不考虑个体差异的MDS模型(ALSCAL),即单个测量个体
②考虑个体差异的MDS模型(INDSCAL),即多个测量个体
这里说的测量个体并不是选取的测量指标,而是实际测量的个体,相当于样本。
由于多维尺度分析是用来分析差异性或相似性的,也带有度量的含义,因此在SPSS中也将其归在了度量过程中。共有三个过程,下面我们来分别介绍
一、不考虑个体差异的MDS模型
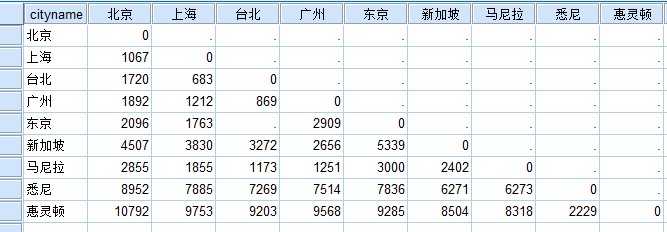
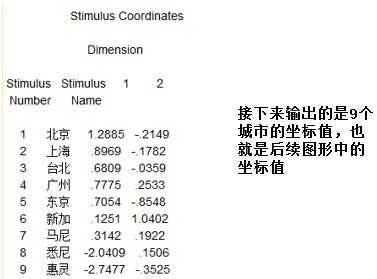
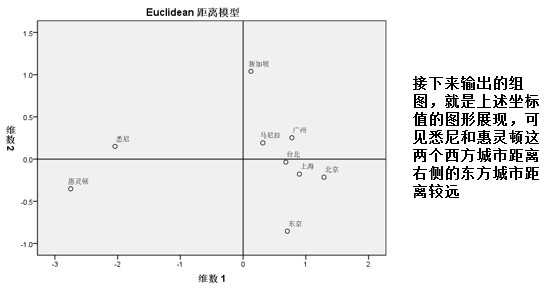
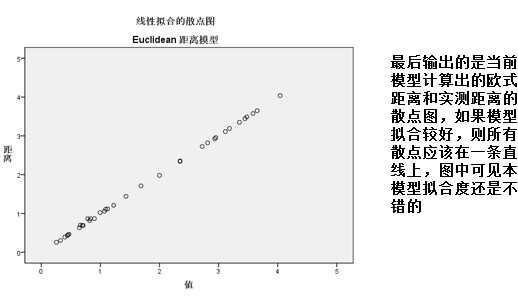
本案例进行的是最基本的多维尺度分析,目的是分析每个城市的距离情况,只有一个个体,并且收集的数据直接是距离数据,因此采用古典MDS模型,数据组成如下
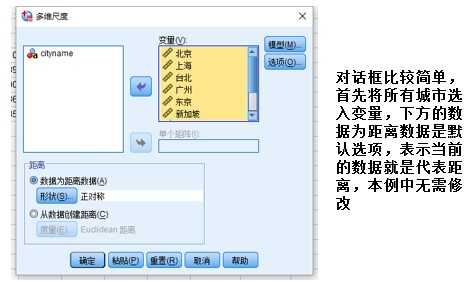
分析—度量—多维尺度(ALSCAL)
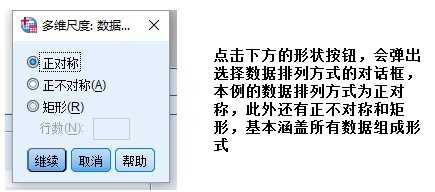


二、考虑个体差异的MDS模型
实际分析中,我们往往不会只选取一个样本,比如受访者肯定不止一个,那么收集上来的数据会变成多个矩阵,如果将其浓缩为一个矩阵会损失大量数据信息,而直接使用重复多维尺度模型当然也是可以的,但是该方法没有考虑个体间差异,因此并非最佳选择。而考虑个体差异的MDS模型不仅分析对象间的结构,而且会进一步分析对象间的差异。
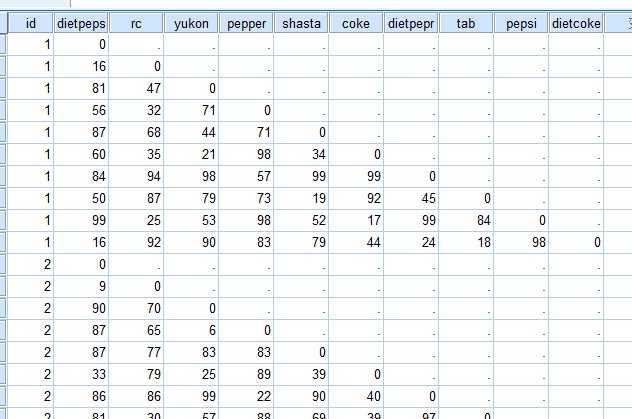
本例中识10位受访者对10种饮料的口感差异性评分,分值越大差异越大,10位受访者的数据形成了10个数据阵,数据如下
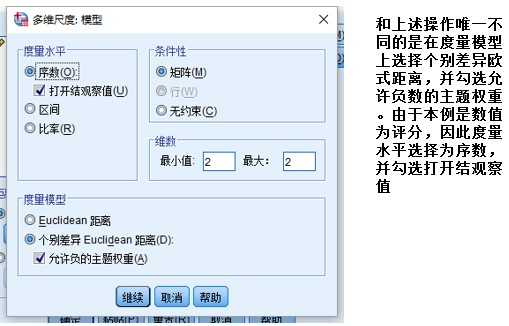
下面我们选用考虑个体差异的MDS模型进行分析
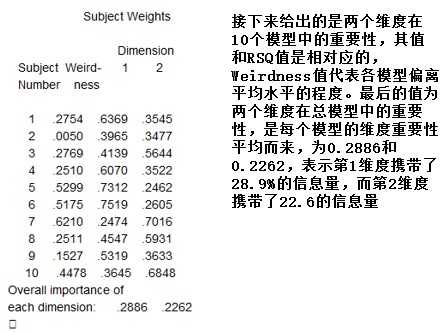

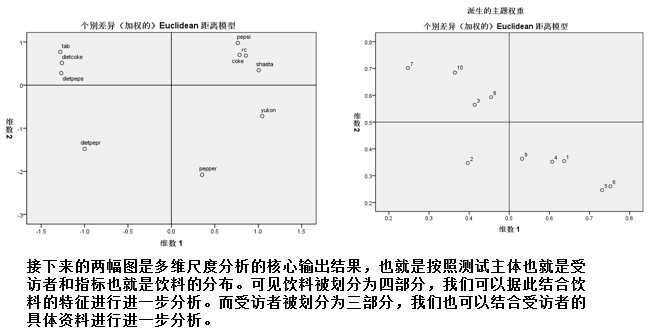
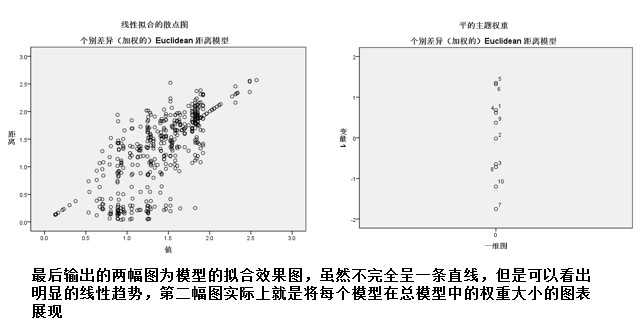
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5654381.html