标签:
基于对概率问题的工具化表征如随机变量、分布列等概念,我们可以开始讨论各种各样的分布列了。(这一章节在书中叫做“随机变量”,但是为了和第五章“连续随机变量”区分开,这里标题写成“离散型随机变量”)
从二项分布结合级数推导而来的泊松分布:
对于二项分布我们很熟悉,在生活当中我们也很常用,但是其计算公式不免显得有点繁琐,我们现进行如下的简化推导:
设某个二项分布的参数是(n,p),设置参数λ=np.随机变量为X.
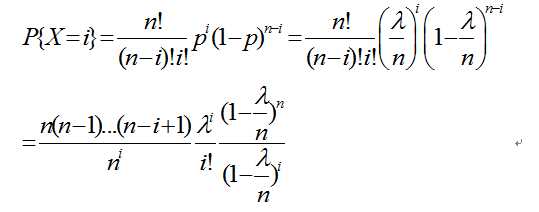
同时结合几种极限求法,我们能够看到,当n趋近于无穷的时候,有:
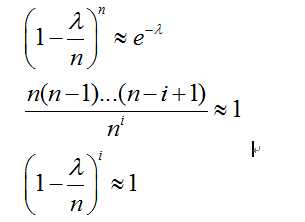
因此我们得到:
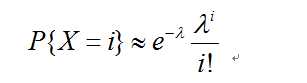
这便是泊松分布列。容易看到,n趋近于无穷的二项分布可以与泊松分布等价,如果基于n趋近于无穷,我们可以验证泊松分布的作为分布列的一个性质:
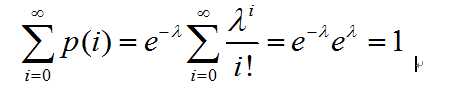
Ps:推导过程用到了泰勒级数的展开式,具体的内容笔者在《托马斯大学微积分》的专栏中会给出。
《A First Course in Probability》-chaper4-离散型随机变量-泊松分布
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5654425.html