标签:
承接之前对一重积分和二重积分的介绍,这里我们自然的引出三重积分。
在二重积分的引入中,我们曾经埋下过一个小伏笔,二重积分的几何意义是求解一个体积,但是我们仅仅限定在了曲顶柱体的几何体,那么对于完全由曲面D包裹的空间D’,我们如何求其体积呢?
我们很自然的能够想到,从x、y、z三个维度作平行线,然后把D’分割成了n个小长方体,如下图。
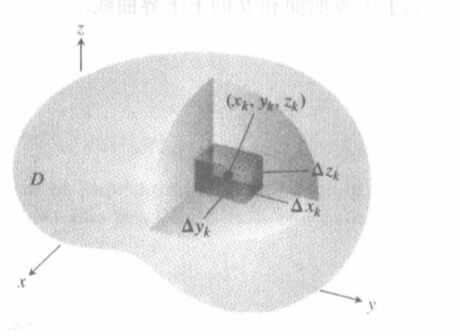
伴随着n趋于无穷,我们可以完美的得到D’区域的体积。
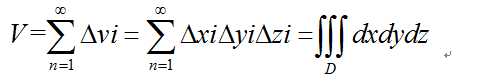
个人认为,这个例子仅仅是为了自然的引出三重积分的概念和形式,在实际应用中,很难通过这个方法来计算各种各样不规则几何体的体积(因为你难以用定义域的形式准确表征边界D),这些东西笔者会在后序的文章中详细介绍。
为了将三重积分的形式和二重积分、一重积分的黎曼和的形式保持一致,我们可以将三重积分表述成如下的黎曼和的形式:
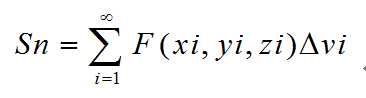
《University Calculus》-chaper13-多重积分-三重积分的引入
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5655265.html