标签:
1. Introduction
Much like Newton‘s method is a standard tool for solving unconstrained smooth minimization problems of modest size, proximal algorithms can be viewed as an analogous tool for nonsmooth, constrained, large-scale, or distributed version of these problems. They are very generally applicable, but they turn out to be especially well-suited to problems of recent and widespread interest involving large or high-dimensional datasets.
Proximal methods sit at a higher level of abstraction than classical optimization algorithms like Newton’s method. In the latter, the base operations are low-level, consisting of linear algebra operations and the computation of gradients and Hessians. In proximal algorithms, the base operation is evaluating the proximal operator of a function, which involves solving a small convex optimization problem. These subproblems can be solved with standard methods, but they often admit closedform solutions or can be solved very quickly with simple specialized methods. We will also see that proximal operators and proximal algorithms have a number of interesting interpretations and are connected to many different topics in optimization and applied mathematics.
2. Algorithms
For following convex optimization problem
$$\min_{x}f(x)+g(x)$$
where $f$ is smooth, $g:R^n\rightarrow R\cup \{+\infty\}$ is closed proper convex.
Generally, there are several proximal methods to solve this problem.
$$x^{k+1}:=prox_{\lambda^kg}(x^k-\lambda^k \nabla f(x^k)$$
which converges with rate $O(1/k)$ when $\nabla f$ is Lipschitz continuous with constant L and step sizes are $ \lambda^k=\lambda\in(0,1/L]$. If $L$ is not known, we can use the following line search:

Typical value of $\beta$ is 1/2, and
$$\hat{f}_{\lambda}(x,y)=f(y)+\nabla f(y)^T(x-y)+(1/2\lambda)||x-y||_{2}^2$$
$$y^{k+1}=x^k+\omega (x^k-x^{k-1})$$
$$x^{k+1}:=prox_{\lambda^kg}(y^{k+1}-\lambda^k \nabla f(y^{k+1}))$$
works for $\omega^k=k/(k+3)$ and similar line search as before.
This method has faster $O(1/k^2)$ convergence rate, originated with Nesterov (1983)
$$x^{k+1}:=prox_{\lambda f}(z^k-u^k)$$
$$z^{k+1}:=prox_{\lambda g}(x^{k+1}+u^k)$$
$$u^{k+1}:=u^k+x^{k+1}-z^{k+1}$$
basiclly, always works and has $O(1/k)$ rate in general. If $f$ and $g$ are both indicators, get a variation on alternating projections.
This method originates from Gabay, Mercier, Glowinski, Marrocco in 1970s.
3. Example
You are required to solve the following optimization problem
$$\min_{x}\frac{1}{2}x^TAx+b^Tx+c+\gamma||x||_{1}$$
where
$$A=\begin{pmatrix} 2 & 0.25 \\ 0.25 & 0.2 \end{pmatrix},\;b=\begin{pmatrix} 0.5 \\ 0.5 \end{pmatrix},\; c=-1.5, \; \lambda=0.2$$
As for this problem, if $f(x)=\frac{1}{2}x^TAx+b^Tx+c$ and $g(x)=\gamma||x||_{1}$ then
$$\nabla f(x)=Ax+b$$
If $g=||\cdot||_{1}$, then
$$prox_{\lambda f}(v)=(v-\lambda)_{+}-(-v-\lambda)_{+}$$
So the update step is
$$x^{k+1}:=prox_{\lambda^k \gamma||\cdot||_{1}}(x^k-\lambda^k \nabla f(x^k))$$
Finally, the 2D coutour plot of objective function and the trajectory of the value update are showed in following figure.
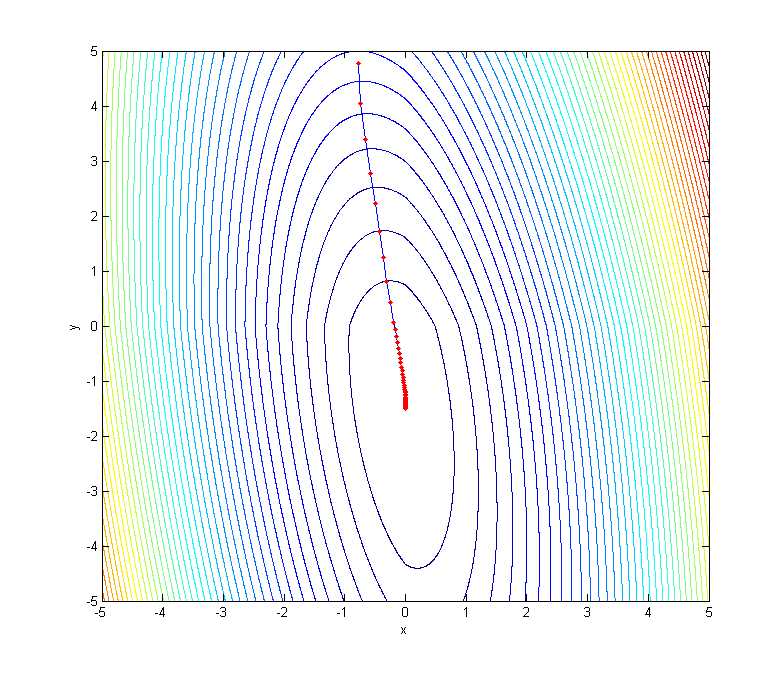
Additionally, when we use proximal gradient method based on exact line search to optimize the objective function, the result is:
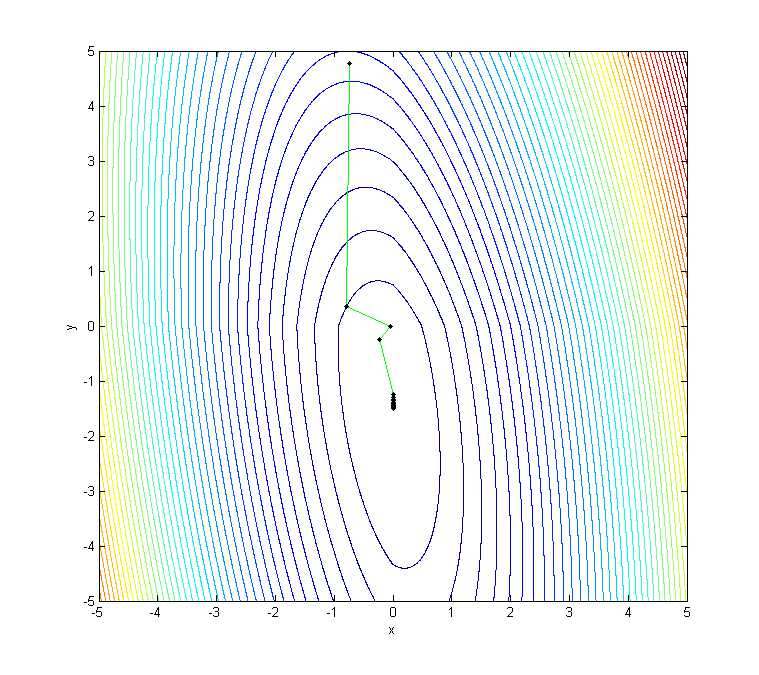
We can find that proximal algorithm can solve this nonsmooth sonvex optimization problem successfully. And method based on exact line search can obtain faster convergence rate than one based on backtracking line search.
If you want to learn proximal algorithms further, you can read the book "Proximal Algorithms" by N. Parikh and S. Boyd, and corresponding website: http://web.stanford.edu/~boyd/papers/prox_algs.html
References
Parikh, Neal, and Stephen P. Boyd. "Proximal Algorithms." Foundations and Trends in optimization 1.3 (2014): 127-239.
标签:
原文地址:http://www.cnblogs.com/huangxiao2015/p/5654754.html